Hexapentakis ścięty dwudziestościan
| Hexapentakis ścięty dwudziestościan | |
|---|---|

|
|
| Notacja Conwaya | ktI |
| Wielościan geodezyjny | {3,5+} 3,0 |
| Twarze | 180 |
| Krawędzie | 270 |
| Wierzchołki | 92 |
| Konfiguracja twarzy |
(60) V5.6.6 (120) V6.6.6 |
| Grupa symetrii | Dwudziestościan ( I h ) |
| Podwójny wielościan | Dwunastościan ścięty pentakis |
| Nieruchomości | wypukły |
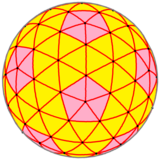
Heksapentakis ścięty dwudziestościan jest wypukłym wielościanem zbudowanym jako powiększony dwudziestościan ścięty . Jest to wielościan geodezyjny {3,5+} 3,0 z wierzchołkami pięciowartościowymi oddzielonymi odległością 3 kroków od krawędzi.
Budowa
Wielościany geodezyjne są konstruowane przez podział ścian prostszych wielościanów, a następnie rzutowanie nowych wierzchołków na powierzchnię kuli. Wielościan geodezyjny ma proste krawędzie i płaskie powierzchnie, które są zbliżone do kuli, ale można go również wykonać jako wielościan sferyczny ( teselacja na kuli ) z prawdziwymi geodezyjnymi zakrzywionymi krawędziami na powierzchni kuli. i sferyczne trójkątne twarze.
| Conway | u 3 ja = (kt) ja | (k5)k6tI | (k)tI | Kulisty ktI |
|---|---|---|---|---|
| Obraz |  |
 |
 |
|
| Formularz |
Dwudziestościan podzielony na 3 częstotliwości |
Dwudziestościan ścięty sześciościan podzielony na 1 częstotliwość |
Dwudziestościan ścięty podzielony na 1 częstotliwość |
Sferyczny wielościan |
Powiązane wielościany
| Wielościan | Dwudziestościan ścięty | #Pentakis obcięty dwudziestościan | #Hexakis obcięty dwudziestościan | Hexapentakis ścięty dwudziestościan |
|---|---|---|---|---|
| Obraz |

|

|

|

|
| Conway | tI | k5tI | k6tI | k5k6tI |
Pentakis ścięty dwudziestościan
| Pentakis ścięty dwudziestościan | |
|---|---|

|
|
| Notacja Conwaya | k5tI |
| Twarze |
132: 60 trójkątów 20 sześciokątów |
| Krawędzie | 90 |
| Wierzchołki | 72 |
| Grupa symetrii | Dwudziestościan ( I h ) |
| Podwójny wielościan | Dwunastościan pentaksowy pięciościanowy |
| Nieruchomości | wypukły |
Pentakis ścięty dwudziestościan to wypukły wielościan zbudowany jako powiększony dwudziestościan ścięty , dodający piramidy do 12 pięciokątnych ścian, tworząc 60 nowych trójkątnych ścian.
Jest geometrycznie podobny do dwudziestościanu , w którym 20 trójkątnych ścian jest podzielonych centralnym sześciokątem i 3 trójkątami narożnymi.
Podwójny
Jego podwójny wielościan można nazwać dwunastościanem pięciokątnym , dwunastościanem , z wierzchołkami powiększonymi przez pięciokątne piramidy, a następnie ścięty wierzchołek tych piramid lub dodanie pięciokątnego pryzmatu do każdej ściany dwunastościanu. Jest to siatka graniastosłupa dwunastościennego .
Hexakis ścięty dwudziestościan
| Hexakis ścięty dwudziestościan | |
|---|---|

|
|
| Notacja Conwaya | k6tI |
| Twarze |
132: 120 trójkątów 12 pięciokątów |
| Krawędzie | 210 |
| Wierzchołki | 80 |
| Grupa symetrii | Dwudziestościan ( I h ) |
| Podwójny wielościan | Dwunastościan pięciościanu sześciokątnego |
| Nieruchomości | wypukły |
Heksakis ścięty dwudziestościan to wypukły wielościan zbudowany jako powiększony dwudziestościan ścięty , dodający piramidy do 20 sześciokątnych ścian, tworząc 120 nowych trójkątnych ścian.
Wizualnie jest podobny do dwunastościanu chiralnego , który ma 80 trójkątów i 12 pięciokątów.
Podwójny
Podwójny wielościan można postrzegać jako sześciościenny dwunastościan pentakisowy , dwunastościan z twarzami powiększonymi przez pięciokątne piramidy ( dwunastościan pentakisowy ), a następnie ścięte wierzchołki 6-falbany.
Ma podobne grupy nieregularnych pięciokątów jak pięciokątny sześcian .
Zobacz też
- Antony Pugh, Wielościany: podejście wizualne , 1976, rozdział 6. Geodezyjne wielościany R. Buckminstera Fullera i pokrewne wielościany
- Wenninger, Magnus (1979), Spherical Models , Cambridge University Press , ISBN 978-0-521-29432-4 , MR 0552023 , zarchiwizowane od oryginału w dniu 4 lipca 2008 r . Przedrukowany przez Dover 1999 ISBN 978-0-486-40921- 4
Linki zewnętrzne
- Generator wielościanów VTML Wypróbuj „ktI” ( notacja wielościanów Conwaya )

