Dwunastościan ścięty pentakis
| Dwunastościan ścięty pentakis | |
|---|---|

|
|
| Notacja Conwaya | tkD |
| Wielościan Goldberga | GP V (3,0) lub {5+,3} 3,0 |
| fuleren | C 180 |
| Twarze |
92: 12 pięciokątów 20+60 sześciokątów |
| Krawędzie | 270 (2 rodzaje) |
| Wierzchołki | 180 (2 rodzaje) |
| Konfiguracja wierzchołków |
(60) 5.6.6 (120) 6.6.6 |
| Grupa symetrii | Dwudziestościan ( I h ) |
| Podwójny wielościan | Pentahexakis ścięty dwudziestościan |
| Nieruchomości | wypukły |
Dwunastościan pięciościanu ściętego jest wypukłym wielościanem skonstruowanym jako obcięcie dwunastościanu pięciościanu . Jest to wielościan Goldberga G V (3,0), z pięciokątnymi ścianami oddzielonymi od krawędzi o 3 stopnie.
Powiązane wielościany
Jest w nieskończonej sekwencji wielościanów Goldberga :
| Indeks | GP(1,0) | GP(2,0) | GP(3,0) | GP(4,0) | GP(5,0) | GP(6,0) | GP(7,0) | GP(8,0)... |
|---|---|---|---|---|---|---|---|---|
| Obraz |
 D |
 kD |
 tkD |

|

|
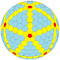
|

|

|
| Podwójne |
 I |
 płyta CD |
 ktI |

|

|
Zobacz też
- Deza, A.; Deza, M .; Grishukhin, V. (1998), „Fullereny i wielościany koordynacyjne a osadzanie pół-sześcianu” , Discrete Mathematics , 192 (1): 41–80, doi : 10.1016 / S0012-365X (98) 00065-X , zarchiwizowane z oryginału w dniu 2007-02-06 .
- Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullereny i wielościany koordynacyjne a osadzanie pół-sześcianu , 1998 PDF [1]
Linki zewnętrzne
- Generator wielościanów VTML Wypróbuj „tkD” ( notacja wielościanów Conwaya )
Kategoria: