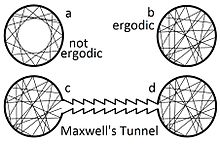
Hipoteza ergodyczna

W fizyce i termodynamice hipoteza ergodyczna mówi, że w długich okresach czas spędzony przez układ w pewnym obszarze przestrzeni fazowej mikrostanów o tej samej energii jest proporcjonalny do objętości tego obszaru, tj. mikrostany są jednakowo prawdopodobne w długim okresie czasu.
Twierdzenie Liouville'a stwierdza, że dla układów hamiltonowskich lokalna gęstość mikrostanów podążających ścieżką cząstki w przestrzeni fazowej jest stała dla obserwatora poruszającego się wraz z zespołem (tj. konwekcyjna pochodna czasu wynosi zero). Tak więc, jeśli mikrostany są równomiernie rozmieszczone w przestrzeni fazowej , pozostaną takie przez cały czas. Ale twierdzenie Liouville'a nie implikuje, że hipoteza ergodyczna obowiązuje dla wszystkich układów hamiltonowskich.
analizie statystycznej fizyki obliczeniowej często przyjmuje się hipotezę ergodyczną . Analityk założyłby, że średnia parametru procesu w czasie i średnia w zespole statystycznym są takie same. To założenie, że równie dobrze jest symulować system przez długi czas, jak wykonać wiele niezależnych realizacji tego samego systemu, nie zawsze jest słuszne. (Patrz na przykład eksperyment Fermi – Pasta – Ulam – Tsingou z 1953 r.)
Przyjęcie hipotezy ergodycznej pozwala udowodnić, że pewne typy perpetuum mobile drugiego rodzaju są niemożliwe.
Mówi się, że systemy, które są ergodyczne, mają własność ergodyczności ; szeroki zakres systemów w geometrii , fizyce i teorii prawdopodobieństwa stochastycznego jest ergodycznych. Systemy ergodyczne są badane w teorii ergodycznej .
Fenomenologia
W systemach makroskopowych skale czasowe, w których system może naprawdę zbadać całą swoją własną przestrzeń fazową, mogą być wystarczająco duże, aby stan równowagi termodynamicznej wykazywał pewną formę złamania ergodyczności . Typowym przykładem jest spontaniczne namagnesowanie w ferromagnetycznych , w którym poniżej temperatury Curie układ preferencyjnie przyjmuje niezerowe namagnesowanie, mimo że hipoteza ergodyczna sugerowałaby, że żadne namagnesowanie netto nie powinno istnieć dzięki systemowi badającemu wszystkie stany, których czas- uśrednione namagnesowanie powinno wynosić zero. Fakt, że układy makroskopowe często naruszają dosłowną postać hipotezy ergodycznej, jest przykładem spontanicznego łamania symetrii .
Jednak złożone układy nieuporządkowane, takie jak szkło wirowe, wykazują jeszcze bardziej skomplikowaną formę łamania ergodyczności, w której właściwości stanu równowagi termodynamicznej widoczne w praktyce są znacznie trudniejsze do przewidzenia wyłącznie na podstawie argumentów symetrii. Również konwencjonalne szkła (np. szyby okienne) łamią ergodyczność w skomplikowany sposób. W praktyce oznacza to, że w wystarczająco krótkich skalach czasowych (np. części sekund, minut, kilku godzin) układy mogą zachowywać się jak ciała stałe, czyli z dodatnim modułem ścinania, ale w ekstremalnie długich skalach, np. przez tysiąclecia czy eony , jako ciecze lub z dwoma lub więcej skalami czasowymi i plateau pomiędzy nimi.
Zobacz też
- Proces ergodyczny
- Teoria ergodyczna , gałąź matematyki zajmująca się bardziej ogólnym sformułowaniem ergodyczności
- Ergodyczność
- Paradoks Loschmidta
- Twierdzenie Poincarégo o powtarzalności