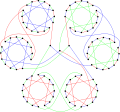
Wykres Hortona

Wykres Hortona
Wykres Hortona
	Wykres Hortona
Nazwany po	Józef Horton
Wierzchołki	96
Krawędzie	144
Promień	10
Średnica	10
Obwód	6
Automorfizmy	; 96 ( Z /2 Z × Z /2 Z × S 4 )
Liczba chromatyczna	2
Indeks chromatyczny	3
Grubość książki	3
Numer kolejki	2
Nieruchomości	; Sześcienny dwudzielny
	Tabela wykresów i parametrów

W matematycznej dziedzinie teorii grafów graf Hortona lub 96-wykres Hortona to 3- regularny graf z 96 wierzchołkami i 144 krawędziami odkrytymi przez Josepha Hortona. Opublikowany przez Bondy'ego i Murty'ego w 1976 roku, stanowi kontrprzykład dla hipotezy Tutte'a, że każdy sześcienny 3-połączony graf dwudzielny jest hamiltonowski .

Po wykresie Hortona znaleziono szereg mniejszych kontrprzykładów do hipotezy Tutte'a. Wśród nich jest graf 92 wierzchołków autorstwa Hortona opublikowany w 1982 r., graf 78 wierzchołków autorstwa Owensa opublikowany w 1983 r. Oraz dwa grafy Ellinghama-Hortona (54 i 78 wierzchołków).

Pierwszy wykres Ellinghama-Hortona został opublikowany przez Ellinghama w 1981 roku i był rzędu 78. W tamtym czasie był to najmniejszy znany kontrprzykład dla hipotezy Tutte'a. Drugi został opublikowany przez Ellinghama i Hortona w 1983 r. I był rzędu 54. W 1989 r. Odkryto graf Georgesa, najmniejszy znany obecnie niehamiltonowski 3-połączony sześcienny graf dwudzielny, zawierający 50 wierzchołków.

Jako niehamiltonowski graf sześcienny z wieloma długimi cyklami, wykres Hortona stanowi dobry punkt odniesienia dla programów poszukujących cykli hamiltonowskich.

Graf Hortona ma liczbę chromatyczną 2, indeks chromatyczny 3, promień 10, średnicę 10, obwód 6, grubość książki 3 i kolejkę numer 2. Jest to również graf 3-krawędziowy .

Właściwości algebraiczne

Grupa automorfizmów grafu Hortona jest rzędu 96 i jest izomorficzna z Z /2 Z × Z _/ 2 Z × S4 , bezpośrednim iloczynem czterogrupy _Kleina i grupy symetrycznej S4 .

Wielomian charakterystyczny wykresu Hortona to: ${\ Displaystyle (x-3) (x-1) ^ {14} x ^ {4} (x + 1) ^ {14} (x + 3) (x ^ {2} -5)^{3}(x^{2}-3)^{11}(x^{2}-x-3)(x^{2}+x-3)}$ ${\ Displaystyle (x ^ {10} -23x ^ {8} + 188x ^ {6} -644x ^ {4} + 803x ^ {2} - 101)^{2}}$ ${\ Displaystyle (x ^ {10} -20x ^ {8} + 143x ^ {6} -437x ^ {4} + 500x ^ {2} -59 )}$ .

Galeria

Liczba chromatyczna wykresu Hortona wynosi 2.
Indeks chromatyczny wykresu Hortona wynosi 3.
Ellinghama -Hortona , mniejszy kontrprzykład dla hipotezy Tutte'a.