Klasyfikator liniowy

W dziedzinie uczenia maszynowego celem klasyfikacji statystycznej jest wykorzystanie cech obiektu do określenia, do której klasy (lub grupy) należy. Klasyfikator liniowy osiąga to, podejmując decyzję klasyfikacyjną na podstawie wartości liniowej kombinacji cech. Charakterystyki obiektu są również znane jako wartości cech i są zwykle przedstawiane maszynie w postaci wektora zwanego wektorem cech . Takie klasyfikatory dobrze sprawdzają się w praktycznych problemach, takich jak klasyfikacja dokumentów , a bardziej ogólnie w przypadku problemów z wieloma zmiennymi ( cechami ), osiągając poziomy dokładności porównywalne z klasyfikatorami nieliniowymi, przy krótszym czasie uczenia się i używania.

Definicja

W tym przypadku pełne i puste kropki można poprawnie sklasyfikować za pomocą dowolnej liczby klasyfikatorów liniowych. H1 (niebieski) klasyfikuje je poprawnie, podobnie jak H2 (czerwony). H2 można uznać za „lepszy” w tym sensie, że jest również najdalszy od obu grup. H3 (zielony) nie potrafi poprawnie sklasyfikować kropek.

Jeśli wejściowy wektor cech do klasyfikatora jest wektorem rzeczywistym , to wynik wyjściowy wynosi ${\ displaystyle {\ vec {x}}}$

{\ Displaystyle y = f ({\ vec {w}} \ cdot {\ vec {x}}) = f \ lewo ( \sum _{j}w_{j}x_{j}\right),}

gdzie ${\ displaystyle {\ vec {w}}}$ jest rzeczywistym wektorem wag, a f jest funkcją, która przekształca iloczyn skalarny dwóch wektorów na żądany wynik. (Innymi słowy, $wagi$ lub liniowym odwzorowaniem funkcjonalnym na $\ displaystyle {\ vec {x}}$ . ) Wektor $} \ displaystyle {\ vec {w}}}$ → uczy się z zestawu oznaczonych próbek treningowych. Często f jest funkcją progową , która $odwzorowuje$ wszystkie wartości powyżej progu na pierwszą klasę, a druga klasa; np,

{\ Displaystyle f (\ mathbf {x}) = {\ rozpocząć {przypadki} 1 i {\ tekst {jeśli}} \ \ mathbf {w} ^ { T}\cdot \mathbf {x} >\theta ,\\0&{\text{inaczej}}\end{przypadki}}}

$Indeks$ górny T wskazuje transpozycję, a progiem skalarnym. Bardziej złożone f może dawać prawdopodobieństwo, że przedmiot należy do określonej klasy.

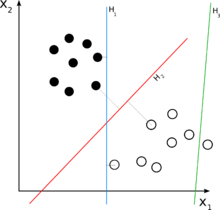
W przypadku problemu klasyfikacji dwuklasowej można zwizualizować działanie klasyfikatora liniowego jako podzielenie wielowymiarowej przestrzeni wejściowej za pomocą hiperpłaszczyzny : wszystkie punkty po jednej stronie hiperpłaszczyzny są klasyfikowane jako „tak”, podczas gdy inne są klasyfikowane jako "NIE".

$w$ których problemem jest szybkość klasyfikacji, ponieważ często jest to najszybszy klasyfikator, zwłaszcza gdy jest rzadki. Ponadto klasyfikatory liniowe często działają bardzo dobrze, gdy liczba wymiarów w $}$ $} }}$ jak w przypadku klasyfikacji dokumentów , gdzie każdy element w to zazwyczaj liczba wystąpień słowa w dokumencie (zobacz macierz terminów w dokumencie ). W takich przypadkach klasyfikator powinien być dobrze uregulowany .

Modele generatywne a modele dyskryminacyjne

Istnieją dwie szerokie klasy metod określania parametrów klasyfikatora liniowego ${\ displaystyle {\ vec {w}}}$ . Mogą to być modele generatywne i dyskryminacyjne . Metody poprzedniego modelu wspólnego rozkładu prawdopodobieństwa , podczas gdy metody drugiego modelują warunkowe funkcje gęstości ${\ Displaystyle P ({\ rm {klasa}} | {\ vec {x}}) }$ . Przykłady takich algorytmów obejmują:

Liniowa analiza dyskryminacyjna (LDA) — zakłada modele gęstości warunkowej Gaussa
Naiwny klasyfikator Bayesa z wielomianowymi lub wielowymiarowymi modelami zdarzeń Bernoulliego.

Drugi zestaw metod obejmuje modele dyskryminacyjne , które próbują zmaksymalizować jakość danych wyjściowych na zbiorze uczącym . Dodatkowe wyrażenia w funkcji kosztu szkolenia mogą łatwo przeprowadzić regularyzację ostatecznego modelu. Przykłady treningu dyskryminacyjnego klasyfikatorów liniowych obejmują:

Regresja logistyczna $,$ oszacowanie maksymalnego prawdopodobieństwa że obserwowany zbiór treningowy został wygenerowany przez model dwumianowy zależny od wyniku klasyfikatora.
Perceptron — algorytm, który próbuje naprawić wszystkie błędy napotkane w zbiorze treningowym
Liniowa analiza dyskryminacyjna Fishera - algorytm (inny niż „LDA”), który maksymalizuje stosunek rozproszenia między klasami do rozproszenia wewnątrz klas, bez żadnych innych założeń. Jest to w istocie metoda redukcji wymiarowości dla klasyfikacji binarnej.
Maszyna wektorów nośnych — algorytm maksymalizujący margines między hiperpłaszczyzną decyzyjną a przykładami w zbiorze uczącym.

Uwaga: Pomimo swojej nazwy, LDA nie należy do klasy modeli dyskryminacyjnych w tej taksonomii. Jednak jego nazwa ma sens, gdy porównamy LDA z innym głównym redukcji wymiarowości liniowej : analizą głównych składowych (PCA). LDA to uczenia nadzorowanego , który wykorzystuje etykiety danych, podczas gdy PCA to algorytm uczenia nienadzorowanego , który ignoruje etykiety. Podsumowując, nazwa jest artefaktem historycznym.

Trening dyskryminacyjny często daje większą dokładność niż modelowanie warunkowych funkcji gęstości ^{[ potrzebne źródło ]} . Jednak obsługa brakujących danych jest często łatwiejsza dzięki modelom gęstości warunkowej ^{[ potrzebne źródło ]} .

Wszystkie wymienione powyżej algorytmy klasyfikatora liniowego można przekształcić w algorytmy nieliniowe działające $innej$ używając sztuczki .

Szkolenie dyskryminacyjne

Trening dyskryminacyjny klasyfikatorów liniowych przebiega zwykle w sposób nadzorowany , za pomocą algorytmu optymalizacyjnego , który otrzymuje zestaw treningowy z pożądanymi wynikami i funkcją strat , która mierzy rozbieżność między wynikami klasyfikatora a pożądanymi wynikami. W ten sposób algorytm uczący rozwiązuje problem optymalizacji postaci

{\ Displaystyle {\ underset {\ mathbf {w}} {\ arg \ min}} \; R (\ mathbf {w} )+C\suma _{i=1}^{N}L(y_{i},\mathbf {w} ^{\mathsf {T}}\mathbf {x} _{i})}

Gdzie

$w$ jest wektorem parametrów klasyfikatora,
$L (y i, w T x i)$ jest funkcją straty, która mierzy rozbieżność między predykcją klasyfikatora a rzeczywistym wyjściem $y i$ dla $i$ -tego przykładu uczącego,
$R (w)$ to funkcja regularyzacyjna , która zapobiega zbyt dużym parametrom (powodującym przeuczenie ) oraz
$C$ jest stałą skalarną (ustawianą przez użytkownika algorytmu uczącego), która kontroluje równowagę między regularyzacją a funkcją straty.

Popularne funkcje strat obejmują utratę zawiasów (dla liniowych SVM) i utratę logarytmiczną (dla liniowej regresji logistycznej). Jeśli funkcja regularyzacji $R$ jest wypukła , to powyższy problem jest wypukły . Istnieje wiele algorytmów rozwiązywania takich problemów; Do popularnych metod klasyfikacji liniowej należą metody ( stochastyczne ) gradientowe , L-BFGS , metody współrzędnych i Newtona .

Zobacz też

Notatki

^ ^abc ^{Guo -}^Xun Yuan; Chia-Hua Ho; Chih-Jen Lin (2012). „Ostatnie postępy w wielkoskalowej klasyfikacji liniowej” (PDF) . proc. IEEE . 100 (9).
^ T. Mitchell, klasyfikatory generatywne i dyskryminacyjne: naiwny Bayes i regresja logistyczna. Wersja robocza, 2005
^ AY Ng i MI Jordania. O klasyfikatorach dyskryminacyjnych i generatywnych: porównanie regresji logistycznej i naiwnego Bayesa. w NIPS 14, 2002.
^ RO Duda, PE Hart, DG Bocian, „Klasyfikacja wzorców”, Wiley, (2001). ISBN 0-471-05669-3
^ RO Duda, PE Hart, DG Bocian, „Klasyfikacja wzorców”, Wiley, (2001). ISBN 0-471-05669-3

Dalsza lektura

Y. Yang, X. Liu, „Ponowne badanie kategoryzacji tekstu”, Proc. Konferencja ACM SIGIR, s. 42–49 (1999). papier @ cytowany
R. Herbrich, „Nauka klasyfikatorów jądra: teoria i algorytmy”, MIT Press, (2001). ISBN 0-262-08306-X

[ieee-1] {Guo -}^Xun Yuan; Chia-Hua Ho; Chih-Jen Lin (2012). „Ostatnie postępy w wielkoskalowej klasyfikacji liniowej” (PDF) . proc. IEEE . 100 (9).

[2] T. Mitchell, klasyfikatory generatywne i dyskryminacyjne: naiwny Bayes i regresja logistyczna. Wersja robocza, 2005

[3] AY Ng i MI Jordania. O klasyfikatorach dyskryminacyjnych i generatywnych: porównanie regresji logistycznej i naiwnego Bayesa. w NIPS 14, 2002.

[4] RO Duda, PE Hart, DG Bocian, „Klasyfikacja wzorców”, Wiley, (2001). ISBN 0-471-05669-3

[5] RO Duda, PE Hart, DG Bocian, „Klasyfikacja wzorców”, Wiley, (2001). ISBN 0-471-05669-3