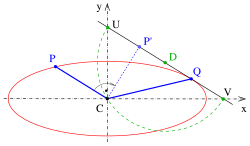
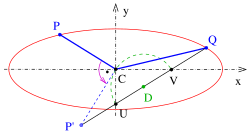
Konstrukcja Rytza

Konstrukcja Rytza: początek - koniec

Konstrukcja osi Rytza jest podstawową metodą geometrii wykreślnej służącą do znajdowania osi, półosi wielkiej i półosi małej oraz wierzchołków elipsy , zaczynając od dwóch sprzężonych półśrednic . Jeśli zostanie określony środek i półoś elipsy, elipsę można narysować za pomocą elipsografu lub ręcznie (patrz elipsa ).

Konstrukcja Rytza jest klasyczną konstrukcją geometrii euklidesowej , w której jako pomoce dozwolone są jedynie kompas i linijka . Projekt nosi imię jego wynalazcy Davida Rytza z Brugg (1801–1868).

Średnice sprzężone pojawiają się zawsze, gdy okrąg lub elipsa są rzutowane równolegle (promienie są równoległe) jako obrazy ortogonalnych średnic okręgu (patrz drugi rysunek) lub jako obrazy osi elipsy. Zasadniczą właściwością dwóch sprzężonych średnic $)$ styczne w punktach elipsy jednej średnicy są równoległe do drugiej średnicy (patrz

Kostka z okręgami: projekcja wojskowa

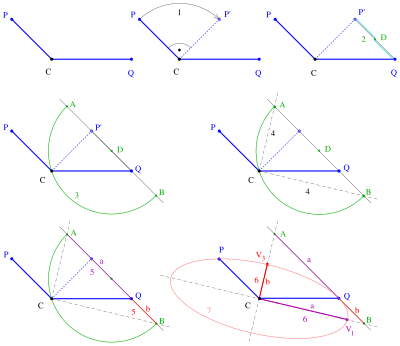
Konstrukcja Rytza w 6 krokach. Dane: środek C i dwie sprzężone średnice połówkowe CP, CQ elipsy. poszukiwane: półosie i wierzchołki elipsy.

Opis problemu i rozwiązanie

Rzut równoległy (pochylony lub ortograficzny) okręgu, który jest ogólnie elipsą (pominięto szczególny przypadek odcinka linii jako obrazu). Podstawowym zadaniem geometrii wykreślnej jest narysowanie takiego obrazu koła. Diagram przedstawia projekcję wojskową sześcianu mającego 3 okręgi na 3 ścianach sześcianu. Płaszczyzna obrazu dla projekcji wojskowej jest pozioma. Oznacza to, że okrąg na górze pojawia się w swoim prawdziwym kształcie (jako okrąg). Obrazy okręgów na pozostałych dwóch ścianach są oczywiście elipsami o nieznanych osiach. Ale w każdym razie rozpoznaje się obrazy dwóch ortogonalnych średnic okręgów. Te średnice elips nie są już ortogonalne, ale jako obrazy ortogonalnych średnic okręgu są sprzężone (styczne w punktach końcowych jednej średnicy są równoległe do drugiej średnicy!). Jest to standardowa sytuacja w geometrii wykreślnej:

• $środek$ elipsy znany jest $i$ dwa punkty
• Zadanie: znaleźć osie i półosie elipsy.

Etapy budowy

$1$ ) obróć punkt wokół $.$ 90 $}$ środek odcinka linii. re $D$$}$ 3) Narysuj linię i okrąg ze środkiem do $displaystyle$$P'Q$

. Przetnij okrąg i linię. Punkty przecięcia to: ${\ displaystyle A, B}$ . $elipsy$ 4 ) Linie $są$ _ _ $elipsa$ ) Segment linii można uznać za pasek papieru o $.$ patrz punkt
${\ displaystyle Q}$ . Stąd ${\ displaystyle a = | AQ |}$ i $są$ półosie . _ (Jeśli za ${\ displaystyle a> b}$$to$ półoś wielka . ) (6) i współwierzchołki są znane, a elipsę można narysować jedną z rysowania .

Jeśli wykona się obrót punktu $schemat$ lewo , konfiguracja przedstawia metodę drugiego paska papieru (patrz drugi w następnej sekcji) i ${\ displaystyle a = | AQ |}$ i ${\ displaystyle b = | BQ |}$ jest nadal prawdą.

Dowód oświadczenia

Rytz: dowód

Dowód standardowy wykonywany jest geometrycznie. Alternatywny dowód wykorzystuje geometrię analityczną:

Dowód jest zakończony, jeśli ktoś jest w stanie to wykazać

• punkty przecięcia $,$ z osiami elipsy leżą na okręgu przechodzącym przez środek P. $displaystyle P'Q}$$, V}$${\ Displaystyle$ , stąd i i $= A}$ U i $B}$${\ Displaystyle | UQ | = a, \ quad | VQ | = b \.}$

Dowód

(1): Dowolną elipsę można przedstawić parametrycznie w odpowiednim układzie współrzędnych za pomocą

${\ Displaystyle {\ vec {p}} (t) = (a \ bo t, \; b \ grzech t) ^ {T}}$ .

Dwa punkty ${\ Displaystyle {\ vec {p}} (t_ {1}), \ {\ vec {p}} (t_ {2})}$ leżą na koniugacie średnice jeśli ${\ Displaystyle t_ {2} -t_ {1} = \ pm {\ tfrac {\ pi} {2}} \.}$ (patrz Elipsa: średnice sprzężone .)

(2): Niech będzie ${\ displaystyle Q = (a \ bo t, \; b \ sin t)$ }

${\ Displaystyle P = (a \ cos (t + {\$

.

Wtedy ${\ Displaystyle P' = (b \ cos t, a \ sin t)}$ i środek odcinka linii ${\ Displaystyle {\ overline {P'Q}} }$ jest ${\ Displaystyle D = \ lewo ({\ tfrac {a + b} {2}} \ cos t, {\ tfrac {a +b}{2}}\sin t\right)}$ .

${\ Displaystyle x \ sin t + y \ bo t = (a + b) \; \ bo t \ grzech t \.}$$t$ ): równanie

Punkty przecięcia tej linii z osiami elipsy to

${\ Displaystyle U = \ lewo (0, \; (a + b) \ sin t \ prawo) \, \ quad V = \ lewo ((a + b) \ cos t, \; 0 \ prawo) \.}$

Rytz: zwrot w lewo punktu ${\ displaystyle P}$

(4): Z powodu $|UD|=|VD|=|CD|}$$Displaystyle$ punkty ${\ displaystyle U, V, C}$ leżą na okręgu o środku promieniu ${\ displaystyle | CD | \.}$

Stąd ${\ Displaystyle A = U, \ B = V \.}$

(5): ${\ Displaystyle | UQ | = a, \ quad | VQ | = b \.}$

W dowodzie zastosowano zwrot punktu w prawo $co$ prowadzi do diagramu przedstawiającego metodę pierwszego paska papieru .

Wariacje

Jeśli wykona się obrót punktu $są$ lewo , wyniki (4) i (5) nadal ważne, a konfiguracja pokazuje teraz metodę drugiego paska papieru (patrz schemat). Jeśli ktoś użyje ${\ Displaystyle P = (a \ cos (t {\ kolor {czerwony} -} \ tfrac {\ pi} {2}}), \; b \ grzech (t {\ kolor {czerwony }-}{\tfrac {\pi }{2}}))=(a\sin t,-b\cos t)}$ , to albo konstrukcja, albo praca próbna.

Rozwiązanie wspomagane komputerowo

Aby znaleźć wierzchołki elipsy za pomocą komputera,

• współrzędne trzech $_$

Prosty pomysł jest następujący: Można napisać program, który wykona kroki opisane powyżej. Lepszym pomysłem jest parametryczne użycie reprezentacji dowolnej elipsy :

• ${\ Displaystyle {\ vec {x}} = {\ vec {p}} (t) = {\ vec {f}} _ {0} + {\ vec {f}} _ {1} \ cos t + {\ vec {f}}_{2}\sin t\ .}$

Z $\ Displaystyle {\ vec {f}} _ {0} = {\ vec {OC}}}$ (w środku) i ${\ Displaystyle {\ vec {f}} _ {1} = {\ vec {CP}}, \; {\ vec {f}} _ {2} = {\ vec {CQ}}} (dwa sprzężone$ pół- średnic) można obliczyć punkty i narysować elipsę.

Jeśli to konieczne: Z ${\ Displaystyle \ łóżeczko (2t_ {0}) = {\ tfrac {{\ vec {f} }_{1}^{\,2}-{\vec {f}}_{2}^{\,2}}{2{\vec {f}}_{1}\cdot {\vec {f }}_{2}}}}$ otrzymujemy cztery wierzchołki elipsy: ${\ Displaystyle {\ vec {p}} (t_ {0}), \; {\ vec {p}} (t_ {0} \ pm {\ Frac {\ pi} {2}}), \; {\ vec {p}}(t_{0}+\pi)\ .}$

•   Rudolf Kurwa; Konrad Kirch; Heinza Nickela (2007). Darstellende Geometrie für Ingenieure [ Geometria wykreślna dla inżynierów ] (w języku niemieckim) (wyd. 17). Monachium: Carl Hanser. P. 183. ISBN 978-3446411432 . Źródło 2013-05-31 .
•   Klaus Ulshöfer; Dietricha Tilpa (2010). „5: Elipsa als ortogonal-affines Bild des Hauptkreises ” [5: „Elipsa jako ortogonalny obraz afiniczny okręgu jednostkowego”]. Darstellende Geometrie in systematischen Beispielen [ Geometria wykreślna w systematycznym zbiorze przykładów ]. Übungen für die gimnastyce Oberstufe (w języku niemieckim) (wyd. 1). Bamberg: CC Buchner. ISBN 978-3-7661-6092-8 .
•   Aleksander Ostermann; Gerharda Wannara (2012). Geometria według swojej historii . Springer Nauka i media biznesowe. s. 68–69. ISBN 9783642291630 .

Linki zewnętrzne

• animacja konstrukcji Rytza