Krzywa Zindlera

Rysunek 1: Krzywa Zindlera. Każdy z cięciw o równej długości przecina krzywą i zamknięty obszar na pół.

Rysunek 2: Przykłady krzywych Zindlera z a = 8 (niebieski), a = 16 (zielony) i a = 24 (czerwony).

Krzywa Zindlera jest prostą zamkniętą krzywą płaską z definiującą właściwością, która:

(L) Wszystkie cięciwy , które przecinają długość krzywej na pół, mają tę samą długość.

Najprostszymi przykładami są okręgi . Austriacki matematyk Konrad Zindler odkrył dalsze przykłady i podał metodę ich konstruowania. Herman Auerbach jako pierwszy użył (w 1938 r.) ustalonej już nazwy krzywa Zindlera .

Auerbach udowodnił, że figura ograniczona krzywą Zindlera io połowie gęstości wody będzie unosić się w wodzie w dowolnym położeniu. Daje to negatywną odpowiedź na dwuwymiarową wersję problemu Stanisława Ulama na pływających ciałach (Zadanie 19 Księgi Szkockiej ), która pyta, czy dysk jest jedyną figurą o jednakowej gęstości, która będzie unosić się w wodzie w dowolnej pozycji (oryginalna problem polega na pytaniu, czy kula jest jedyną bryłą mającą tę właściwość w trzech wymiarach).

Z krzywymi Zindlera wiąże się również problem ustalenia, czy możliwe jest wyznaczenie kierunku ruchu roweru przy zamkniętych tylko tylnych i przednich torach.

Równoważne definicje

Równoważna definicja krzywej Zindlera jest następująca:

(A) Wszystkie cięciwy , które przecinają obszar na pół, mają tę samą długość.

Te akordy są takie same, co przecina długość krzywej na pół.

Inna definicja opiera się na karuzeli Zindlera z dwoma krzesłami. Rozważmy dwie gładkie krzywe w R ² określone przez λ ₁ i λ ₂ . Załóżmy, że odległość między punktami λ ₁ (t) i λ ₂ (t) jest stała dla każdego t ∈ R i że krzywa zdefiniowana przez punkty środkowe między λ ₁ i λ ₂ jest taka, że jej wektor styczny w punkcie t jest równoległy do odcinka od λ ₁ ( t ) do λ ₂ ( t ) dla każdego t . Jeżeli krzywe λ ₁ i λ ₂ parametryzują tę samą gładką krzywą zamkniętą, to ta krzywa jest krzywą Zindlera.

Przykłady

Rozważmy stały parametr rzeczywisty ${\ displaystyle a}$ . Dla $_$ _

\ Displaystyle z (u) = x(u)+iy(u)=e^{2iu}+2e^{-iu}+ae^{iu/2}\;,\ u\w [0,4\pi ]\;,}

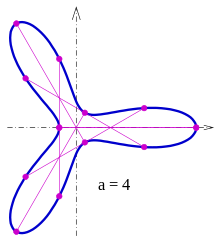
jest krzywą Zindlera. Dla $24}$ krzywa jest nawet wypukła . Diagram $zielony$ $)$ $)$ , ( i Dla $krzywą$ są powiązane z stałej .

Rysunek 3: Przykładowa krzywa z a=4 NIE jest krzywą Zindlera, ponieważ istnieją pożądane cięciwy, które przecinają krzywą w trzecim punkcie.

Dowód (L) : Pochodna równania parametrycznego wynosi

{\ Displaystyle Z' (u) = ja {\ duży (} 2e ^ {2iu} -2e ^{-iu}+{\frac {a}{2}}e^{iu/2}{\Duży)}\;}

i

{\ Displaystyle | z' (u) | ^ {2} = z' (u) {\ overline {z' (u)}} = \ cdots = 8 + {\ Frac {a ^ {2}} {4} }-8\cos 3u\;.}

${\ Displaystyle | z' (u) |}$ jest ${\ Displaystyle 2 \ pi}$ - okresowo . Stąd dla każdego $następujące$ równanie

{\ Displaystyle \ int _ {u_ {0}} ^ {u_ {0} + 2 \ pi} | z' (u) | \, du = \ int _ {0} ^ {2 \ pi} | z'(u)|\,du\;,}

co stanowi połowę długości całej krzywej. Pożądane akordy, które dzielą krzywą na pół, są ograniczone punktami ${\ Displaystyle \; z (u_ {0}) \;, \; z (u_ {0} +2 \ pi ) \;}$ dla dowolnego ${\ Displaystyle u_ {0} \ w [0,4 \ pi]}$ . Długość takiego akordu to ${\ Displaystyle | z (u_ {0} + 2 \ pi) -z (u_ {0}) | = \ cdots = | 2ae ^ {iu_ {0}/2} | = 2a \;,}$ stąd niezależny od ${\ displaystyle u_ {0}}$ . ∎

Dla $pożądane akordy stykają się$ w dodatkowym punkcie (patrz rysunek 3) Stąd tylko dla $krzywych$ krzywe Zindlera.

Uogólnienia

Właściwość definiującą krzywe Zindlera można również uogólnić na cięciwy przecinające obwód krzywej w stałym stosunku α różnym od 1/2. W takim przypadku można rozważyć system akordów (ciągły wybór akordów) zamiast wszystkich akordów krzywej. Krzywe te są znane jako krzywe α-Zindlera i są krzywymi Zindlera dla α = 1/2. To uogólnienie krzywej Zindlera ma następującą właściwość związaną z problemem płynięcia: niech γ będzie zamkniętą gładką krzywą z układem cięciw przecinającym obwód w ustalonym stosunku α. Jeśli wszystkie akordy tego układu akordów znajdują się wewnątrz obszaru ograniczonego przez γ, to γ jest krzywą α-Zindlera wtedy i tylko wtedy, gdy obszar ograniczony przez γ jest bryłą o jednolitej gęstości ρ, która unosi się w dowolnej orientacji.

Zobacz też

Notatki

Bibliografia _ Lewi, Marek; Perline, Ron; Tabachnikow, Siergiej (2018). „Ślady opon i całkowalna ewolucja krzywej” . Zawiadomienia o Międzynarodowych Badaniach Matematycznych . 2020 (9): 2698–2768. doi : 10.1093/imrn/rny087 .
Bibliografia _ Montejano L.; Oliveros, D. (2004-12-01). „Karuzele, krzywe Zindlera i problem unoszącego się ciała”. Periodica Mathematica Hungarica . 49 (2): 9–23. CiteSeerX 10.1.1.542.926 . doi : 10.1007/s10998-004-0519-6 . ISSN 0031-5303 . S2CID 8229876 .
^ W. Wunderlich: Algebraische Beispiele ebener und räumlicher Zindler-Kurven . Publikacja Matematyka Debreczyn 24 (1977), 289–297. (S. 291).
^ ^ab ^Bracho , J.; Montejano L.; Oliveros, D. (2001-07-01). „Twierdzenie o klasyfikacji karuzeli Zindlera”. Journal of Dynamical and Control Systems . 7 (3): 367–384. doi : 10.1023/A:1013099830164 . ISSN 1079-2724 . S2CID 116492433 .

Herman Auerbach: Sur un problème de M. Ulama dotyczy l'équilibre des corps flottants (PDF; 796 kB) , Studia Mathematica 7 (1938), 121–142.
KL Mampel: Über Zindlerkurven , Journal für reine und angewandte Mathematik 234 (1969), 12–44.
Konrad Zindler: Über convexe Gebilde. II. Teil , Monatshefte für Mathematik und Physik 31 (1921), 25–56.
H. Martini, S. Wu: O krzywych Zindlera w płaszczyznach znormalizowanych , Canadian Mathematical Bulletin 55 (2012), 767–773.
J. Bracho, L. Montejano, D. Oliveros: Karuzele, krzywe Zindlera i problem unoszącego się ciała , Periodica Mathematica Hungarica 49 (2004), 9–23.
PM Gruber, JM Wills: wypukłość i jej zastosowania , Springer, 1983, ISBN 978-3-0348-5860-1 , s. 58.

Linki zewnętrzne

http://www.thphys.uni-heidelberg.de/~wegner/Fl2mvs/Movies.html — strona autorstwa Franza Wegnera ilustrująca niektóre ciała unoszące się w dowolnym kierunku.
https://www.rose-hulman.edu/~finn/research/bicycle/tracks.html - Strona autorstwa Davida L. Finna ilustrująca parę krzywych, których nie można określić, która z nich jest torem tylnym, a który przednim roweru.

[1] Bibliografia _ Lewi, Marek; Perline, Ron; Tabachnikow, Siergiej (2018). „Ślady opon i całkowalna ewolucja krzywej” . Zawiadomienia o Międzynarodowych Badaniach Matematycznych . 2020 (9): 2698–2768. doi : 10.1093/imrn/rny087 .

[2] Bibliografia _ Montejano L.; Oliveros, D. (2004-12-01). „Karuzele, krzywe Zindlera i problem unoszącego się ciała”. Periodica Mathematica Hungarica . 49 (2): 9–23. CiteSeerX 10.1.1.542.926 . doi : 10.1007/s10998-004-0519-6 . ISSN 0031-5303 . S2CID 8229876 .

[3] W. Wunderlich: Algebraische Beispiele ebener und räumlicher Zindler-Kurven . Publikacja Matematyka Debreczyn 24 (1977), 289–297. (S. 291).

[Bracho_2001-4] Bracho , J.; Montejano L.; Oliveros, D. (2001-07-01). „Twierdzenie o klasyfikacji karuzeli Zindlera”. Journal of Dynamical and Control Systems . 7 (3): 367–384. doi : 10.1023/A:1013099830164 . ISSN 1079-2724 . S2CID 116492433 .