Księżyc (geometria)



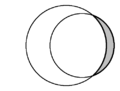
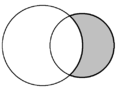
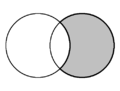
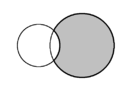
W geometrii płaskiej kształt półksiężyca utworzony przez dwa przecinające się koła nazywa się księżycem . Na każdym diagramie obecne są dwa księżyce, a jeden jest zacieniony na szaro.

W geometrii płaszczyzny lune (z łac. luna „księżyc”) to obszar wklęsło-wypukły ograniczony dwoma okrągłymi łukami . Ma jedną część graniczną, dla której segment łączący dowolne dwa pobliskie punkty przesuwa się poza region, oraz drugą część graniczną, dla której segment łączący dowolne dwa pobliskie punkty leży całkowicie wewnątrz regionu. Obszar wypukły-wypukły nazywany jest soczewką .

Formalnie lune jest względnym uzupełnieniem jednego dysku w drugim (gdzie się przecinają, ale żaden nie jest podzbiorem drugiego). $Alternatywnie$ $_$ jeśli i to $.$ _

Kwadratura księżyca

W V wieku pne Hipokrates z Chios wykazał, że Księżyc Hipokratesa i dwa inne księżyce można dokładnie podnieść do kwadratu (zamienić na kwadrat o tym samym polu) za pomocą liniału i kompasu . W 1766 roku fiński matematyk Daniel Wijnquist, cytując Daniela Bernoulliego , wymienił wszystkie pięć geometrycznych kwadratów księżyców, dodając je do tych znanych przez Hipokratesa. W 1771 roku Leonard Euler podał ogólne podejście i uzyskał pewne równanie problemu. W 1933 i 1947 udowodnił to Nikołaj Czebotariow i jego uczeń Anatolij Dorodnow, że te pięć to jedyne kwadratowe luny.

Obszar

Pole księżyca utworzone przez okręgi o promieniach a i b ( b>a ) o odległości c między ich środkami wynosi

{\ Displaystyle A = 2 \ Delta + a ^ {2} \ sec ^ {-1} \ lewo ({\ Frac {2ac} {b ^ {2} -a ^ {2} -c ^ {2}}} \right)-b^{2}\sec ^{-1}\left({\frac {2bc}{b^{2}+c^{2}-a^{2}}}\right),}

gdzie ${\ Displaystyle {\ tekst {sec}} ^ {- 1}}$ jest funkcją odwrotną funkcji siecznej i gdzie

{\ Displaystyle \ Delta = {\ Frac {1} {4}} { \sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+bc)}}}

jest polem trójkąta o bokach a, b i c .

Zobacz też

Linki zewnętrzne

Pięć kwadratowych księżyców na MathPages