Kwadratowa nieograniczona optymalizacja binarna
Kwadratowa nieograniczona optymalizacja binarna ( QUBO ), znana również jako binarne programowanie kwadratowe bez ograniczeń ( UBQP ), to problem optymalizacji kombinatorycznej o szerokim zakresie zastosowań, od finansów i ekonomii po uczenie maszynowe . QUBO jest NP trudnym i dla wielu klasycznych problemów z informatyki teoretycznej , takich jak maksymalne cięcie , kolorowanie grafów i problem podziału , sformułowano osadzania w QUBO. Osadzanie modeli uczenia maszynowego obejmuje maszyny wektorów nośnych , grupowanie i probabilistyczne modele graficzne . Co więcej, ze względu na bliskie powiązanie z modelami Isinga , QUBO stanowi centralną klasę problemów w adiabatycznych obliczeniach kwantowych , gdzie jest rozwiązywana za pomocą procesu fizycznego zwanego wyżarzaniem kwantowym .
Definicja
Zbiór binarnych stałej długości , gdzie to zbiór wartości binarnych (lub bitów ). Otrzymujemy macierz rzeczywistych zdefiniuj wagę dla każdej pary indeksów \ wektor binarny. Możemy zdefiniować funkcję, która przypisuje wartość każdemu wektorowi binarnemu poprzez
Intuicyjnie wagę dodaje się, jeśli zarówno jak i 1. Kiedy , wartości dodawane, jeśli jako dla wszystkich }
Problem QUBO polega na znalezieniu wektora binarnego , który jest minimalny w do , a mianowicie :
Ogólnie rzecz biorąc, nie jest unikalny, co oznacza może istnieć zbiór wektorów minimalizujących o równej wartości wrt . Złożoność QUBO wynika z liczby kandydatów na wektory binarne, które należy ocenić, jako rośnie wykładniczo w }
problem maksymalizacji równoważne _
Nieruchomości
- współczynników przez dodatni odpowiednio wynik optymalne. bez zmian:
- odwrócenie znak , binarny maksymalizuje fa
- Jeśli wszystkie współczynniki są dodatnie, optymalne jest trywialnie. . Podobnie, jeśli wszystkie współczynniki są ujemne, optymalne jest .
- Jeśli , tj . bity można optymalizować niezależnie, to odpowiedni problem QUBO można rozwiązać w , optymalne przypisania zmiennych wynoszą po prostu 1, jeśli i 0 w przeciwnym razie.
Aplikacje
QUBO jest strukturalnie prostym, ale trudnym obliczeniowo problemem optymalizacyjnym. Można go wykorzystać do kodowania szerokiej gamy problemów optymalizacyjnych z różnych dziedzin nauki.
Analiza skupień
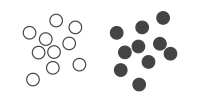
Jako ilustrujący przykład wykorzystania QUBO do kodowania problemu optymalizacyjnego rozważymy problem analizy skupień . Tutaj mamy zbiór 20 punktów w przestrzeni 2D, opisany zawiera kartezjańskie współrzędne . Chcemy przypisać każdy punkt do jednej z dwóch klas lub skupień , tak aby punkty w tym samym skupieniu były do siebie podobne. Dwóm skupieniom możemy przypisać zmienną binarną do punktu odpowiadającego -temu re wskazując, czy należy on do pierwszego ( ) lub drugi klaster ( ). W rezultacie mamy 20 zmiennych binarnych, które tworzą wektor binarny. co odpowiada przypisaniu klastra wszystkich punktów (patrz rysunek).
Jednym ze sposobów uzyskania grupowania jest rozważenie odległości między punktami parami. Biorąc pod uwagę przypisanie klastra wartości lub 1 ocenia się na 1, jeśli punkty znajdują się w tym samym klastrze. Podobnie lub x_ są w różnych skupiskach. Niech oznacza odległość euklidesową między punktami re ja . Aby zdefiniować funkcję kosztu do minimalizacji, gdy punkty i dodajemy ich odejmujemy gdy znajdują się w różnych skupiskach. W ten sposób optymalne rozwiązanie ma tendencję do umieszczania punktów, które są daleko od siebie, w różnych skupieniach, a punkty, które są blisko, w tym samym skupieniu. Funkcja kosztu sprowadza się zatem do
Z drugiej linii parametry QUBO można łatwo znaleźć, zmieniając ich kolejność na:
Korzystając z tych parametrów, optymalne rozwiązanie QUBO będzie odpowiadać optymalnemu klasterowi wrt powyżej funkcji kosztu.
Połączenie z modelami Ising
QUBO jest bardzo blisko spokrewnione i obliczeniowo równoważne z modelem Isinga , którego funkcja Hamiltona jest zdefiniowana jako
z parametrami o wartościach rzeczywistych dla wszystkich . Zmienne spinowe z wartościami σ . Co więcej której tylko sąsiednie pary zmiennych mieć niezerowe współczynniki. Zastosowanie tożsamości daje równoważny problem QUBO:
Gdzie
Ponieważ stała nie zmienia położenia optymalnego ją pominąć podczas optymalizacji i jest ważna tylko dla odzyskania pierwotnej wartości
Linki zewnętrzne
- QUBO Benchmark (benchmark pakietów oprogramowania do dokładnego rozwiązania QUBO; część dobrze znanej kolekcji testów porównawczych Mittelmann)
- Endre Boros, Peter L Hammer i Gabriel Tavares (kwiecień 2007). „Lokalne heurystyki wyszukiwania dla kwadratowej nieograniczonej optymalizacji binarnej (QUBO)” . Dziennik heurystyki . Stowarzyszenie Maszyn Obliczeniowych. 13 (2): 99–132. doi : 10.1007/s10732-007-9009-3 . S2CID 32887708 . Źródło 12 maja 2013 r .
- Di Wang i Robert Kleinberg (listopad 2009). „Analiza kwadratowych problemów optymalizacji binarnej bez ograniczeń za pośrednictwem przepływów wielu towarów” . Dyskretna matematyka stosowana . Elsevier. 157 (18): 3746–3753. doi : 10.1016/j.dam.2009.07.009 . PMC 2808708 . PMID 20161596 .














































![{\displaystyle {\begin{aligned}f(x)&=\sum _{i<j}d_{ij}(x_{i}x_{j}+(1-x_{i})(1-x_{j}))-d_{ij}(x_{i}(1-x_{j})+(1-x_{i})x_{j})\\&=\sum _{i<j}\left[4d_{ij}x_{i}x_{j}-2d_{ij}x_{i}-2d_{ij}x_{j}+d_{ij}\right]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f46ef423537d3084fa6228aa3b293c924af3b5ac)











