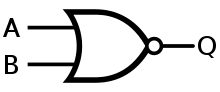
Logika NOR

Ten artykuł dotyczy logiki NOR w sensie budowania innych bramek logicznych przy użyciu tylko bramek NOR. W przypadku bramek NOR patrz bramka NOR . Aby zapoznać się z NOR w sensie czysto logicznym, zobacz Logiczne NOR . Aby zapoznać się ogólnie z bramkami logicznymi, zobacz Bramka logiczna .

Pojedyncza bramka NOR

Bramka NOR lub bramka NOT OR to bramka logiczna, która daje dodatnie wyjście tylko wtedy, gdy oba wejścia są ujemne.

Podobnie jak bramki NAND , bramki NOR są tak zwanymi „bramkami uniwersalnymi”, które można łączyć, tworząc dowolny inny rodzaj bramki logicznej . Na przykład pierwszy system wbudowany , Apollo Guidance Computer , został zbudowany wyłącznie z bramek NOR, w sumie około 5600 dla późniejszych wersji. Obecnie układy scalone nie są budowane wyłącznie z jednego rodzaju bramki. Zamiast tego EDA są używane do konwersji opisu obwodu logicznego na listę sieci złożonych bramek ( komórek standardowych ) lub tranzystorów ( pełne niestandardowe podejście).

ANI

Główny artykuł: bramka NOR

Bramka NOR jest logicznie odwróconą bramką OR. Ma następującą tabelę prawdy:

Q = A NOR B Tabela prawdy Wejście A Wejście B Wyjście Q 0 0 1 0 1 0 1 0 0 1 1 0

Tworzenie innych bramek za pomocą bramek NOR

Bramka NOR jest bramką uniwersalną, co oznacza, że ​​każda inna bramka może być reprezentowana jako kombinacja bramek NOR.

NIE

Zobacz też: bramka NOT

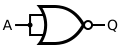
Odbywa się to poprzez połączenie wejść bramki NOR. Ponieważ bramka NOR jest równoważna bramce OR prowadzącej do bramki NOT, połączenie wejść sprawia, że ​​wyjście części „OR” bramki NOR jest takie samo jak wejście, eliminując je z rozważań i pozostawiając tylko część NOT.

Pożądana bramka NOT	NOR Budownictwo
Q = NIE( ZA )	= A NIE A
Tabela prawdy Wejście A Wyjście Q 0 1 1 0

LUB

Zobacz też: bramka OR

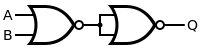
Bramka OR jest tworzona przez odwrócenie wyjścia bramki NOR. Zauważ, że już wiemy, że bramka NOT jest równoważna bramce NOR z połączonymi wejściami.

Pożądana bramka OR	NOR Budownictwo
Q = A LUB B	= ( ZA ANI B ) ANI ( ZA ANI B )
Tabela prawdy Wejście A Wejście B Wyjście Q 0 0 0 0 1 1 1 0 1 1 1 1

I

Zobacz też: bramka AND

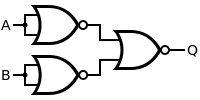
Bramka AND daje wyjście 1, gdy oba wejścia są równe 1. Dlatego bramka AND jest tworzona przez odwrócenie wejść bramki NOR. Ponownie zauważ, że bramka NOT jest równoważna bramce NOR z połączonymi wejściami.

Pożądana bramka AND	NOR Budownictwo
Q = A I B	= ( ZA ANI ZA ) ANI ( B ANI B )
Tabela prawdy Wejście A Wejście B Wyjście Q 0 0 0 0 1 0 1 0 0 1 1 1

NAND

Zobacz też: bramka NAND

Bramka NAND jest tworzona przez odwrócenie wyjścia bramki AND. Słowo NAND oznacza, że ​​nie jest to AND. Jak sama nazwa wskazuje, da 0, gdy oba wejścia mają wartość 1.

Pożądana bramka NAND	NOR Budownictwo
Q = A NAND B	= [ ( ZA ANI ZA ) ANI ( B ANI B ) ] ANI [ ( A ANI A ) ANI ( B ANI B ) ]
Tabela prawdy Wejście A Wejście B Wyjście Q 0 0 1 0 1 1 1 0 1 1 1 0

XNOR

Zobacz też: bramka XNOR

Bramka XNOR jest tworzona przez połączenie czterech bramek NOR, jak pokazano poniżej. Ta konstrukcja pociąga za sobą trzykrotne opóźnienie propagacji w porównaniu z pojedynczą bramką NOR.

Pożądana bramka XNOR	NOR Budownictwo
Q = A XNOR B	= [ ZA NOR ( A NOR B ) ] NOR [ B NOR ( A NOR B ) ]
Tabela prawdy Wejście A Wejście B Wyjście Q 0 0 1 0 1 0 1 0 0 1 1 1

Alternatywnie, bramka XNOR jest tworzona przez rozważenie koniunkcyjnej postaci normalnej ${\ Displaystyle (A + {\ overline {B}}) \ cdot ({\ overline {A}} + B)}$ , zauważając z prawa de Morgana , że ​​bramka NOR jest bramką AND z odwróconym wejściem. Ta konstrukcja wykorzystuje pięć bramek zamiast czterech.

Pożądana Brama	NOR Budownictwo
Q = A XNOR B	= [ B NOR ( A NOR A ) ] NOR [ A NOR ( B NOR B ) ]

XOR

Zobacz też: bramka XOR

Bramka XOR jest tworzona przez rozważenie koniunkcyjnej postaci normalnej ${\ Displaystyle (A + B) \ cdot ({\ overline {A}} + {\ overline {B}} )}$ , zauważając z prawa de Morgana , że ​​bramka NOR jest bramką OR z odwróconym wejściem. Ta konstrukcja pociąga za sobą trzykrotne opóźnienie propagacji w porównaniu z pojedynczą bramką NOR i wykorzystuje pięć bramek.

Pożądana bramka XOR	NOR Budownictwo
Q = XOR B _	= [ ( ZA ANI ZA ) ANI ( B ANI B ) ] ANI ( A ANI B )
Tabela prawdy Wejście A Wejście B Wyjście Q 0 0 0 0 1 1 1 0 1 1 1 0

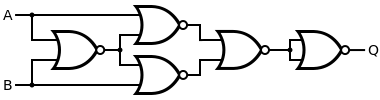
Alternatywnie, 4-bramkowa wersja bramki XNOR może być używana z falownikiem. Ta konstrukcja ma czterokrotnie (zamiast trzykrotnie) opóźnienie propagacji w porównaniu z pojedynczą bramką NOR.

Pożądana Brama	NOR Budownictwo
Q = XOR B _	= { [ ZA NOR ( A NOR B ) ] ANI [ B NOR ( A NOR B ) ] } ANI { [ ZA NOR ( A NOR B ) ] ANI [ b NOR ( A NOR B ) ] }

Zobacz też

• Logika NAND — podobnie jak bramki NOR, bramki NAND są również bramkami uniwersalnymi.
• Funkcjonalna kompletność