Bramka XNOR

Wejście		Wyjście
A	B	XNOR B
0	0	1
0	1	0
1	0	0
1	1	1

Bramka XNOR (czasami ENOR , EXNOR lub NXOR i wymawiana jako Exclusive NOR . Alternatywnie XAND , wymawiana Exclusive AND ) jest cyfrową bramką logiczną , której funkcja jest logicznym uzupełnieniem bramki Exclusive OR ( XOR ). Jest to odpowiednik logicznego spójnika ( ) $z$ matematycznej , znany również jako materiał dwuwarunkowy. Wersja dwuwejściowa implementuje równość logiczną , zachowując się zgodnie z tabelą prawdy po prawej stronie, dlatego bramka jest czasami nazywana „bramką równoważności”. Wysokie wyjście (1) pojawia się, gdy oba wejścia do bramki są takie same. Jeśli jedno, ale nie oba wejścia są w stanie wysokim (1), na wyjściu pojawia się stan niski (0).

Notacja algebraiczna używana do reprezentowania operacji XNOR to ${\ Displaystyle S = A \ odot B}$ ZA Wyrażenia algebraiczne ${\ Displaystyle (A + {\ overline {B}}) \ cdot ({\ overline {A}} + B)}$ i ${\ Displaystyle A \ cdot B + {\ overline {A}} \ cdot {\ overline {B}}}$ oba reprezentują bramkę XNOR z wejściami A i B .

Symbolika

Istnieją dwa symbole bramek XNOR : jeden o charakterystycznym kształcie i jeden o prostokątnym kształcie i etykiecie. Oba symbole bramki XNOR są symbolami bramki XOR z dodanym bąbelkiem inwersji.

Charakterystyczny symbol

Symbol prostokąta

Opis sprzętu

Bramki XNOR są reprezentowane w większości rodzin układów scalonych TTL i CMOS . Standardowy serii 4000 to układ 4077, a układ scalony TTL to układ 74266 (chociaż implementacja z otwartym kolektorem ). Oba zawierają cztery niezależne, dwuwejściowe bramki XNOR. W (obecnie przestarzałym) 74S135 zaimplementowano cztery dwuwejściowe bramki XOR / XNOR lub dwie trzywejściowe bramki XNOR.

Zarówno implementacja TTL 74LS , 74LS266, jak i bramki CMOS (CD4077, 74HC4077 i 74HC266 itp . ) oraz formaty SOIC (SOIC-14, SOC-14 lub TSSOP-14).

Arkusze danych są łatwo dostępne w większości baz danych arkuszy danych i u dostawców.

Pinout

Oba urządzenia 4077 i 74x266 (SN74LS266, 74HC266, 74266 itd.) mają ten sam schemat pinów, jak następuje:

Schemat pinów układów scalonych 74HC266N, 74LS266 i CD4077 quad XNOR z podwójną obudową z tworzywa sztucznego w obudowie 14-stykowej ( PDIP-14 ) .

Wejście A1
Wejście B1
Wyjście Q1 (stan wysoki wtedy i tylko wtedy, gdy A1 i B1 mają ten sam poziom logiczny)
Wyjście Q2
Wejście B2
Wejście A2
V _ss (GND) wspólny styk uziemienia zasilania i sygnału
Wprowadź A3
Wejście B3
Wyjście Q3
Wyjście Q4
Wejście B4
Wprowadź A4
Zasilanie dodatnie V _dd dla CMOS (V _{cc dla TTL) (dopuszczalne zakresy napięć podano w arkuszach danych)}

Alternatywy

Obwód bramki XNOR wykorzystujący trzy mieszane bramki

Jeśli określony typ bramki nie jest dostępny, obwód realizujący tę samą funkcję można zbudować z innych dostępnych bramek. Obwód implementujący funkcję XNOR można w prosty sposób zbudować z bramki XOR, po której następuje bramka NOT. Jeśli weźmiemy pod uwagę wyrażenie ${\ Displaystyle (A + {\ overline {B}}) \ cdot ({\ overline {A}} + B)} ,$ możemy skonstruować Obwód bramki XNOR bezpośrednio przy użyciu bramek AND, OR i NOT. Jednak to podejście wymaga pięciu bramek trzech różnych rodzajów.

Alternatywnie, jeśli dostępne są różne bramki, możemy zastosować algebrę Boole'a do przekształcenia ${\ Displaystyle (A + {\ overline {B}})\cdot ({\overline {A}}+B)\equiv (A\cdot B)+({\overline {A}}\cdot {\overline {B}})} jak podano powyżej$ , i zastosować prawo de Morgana do ostatniego terminu, aby uzyskać ${\ Displaystyle (A \ cdot B) + {\ overline {(A + B)}}},$ które można zaimplementować przy użyciu tylko trzech bramek, jak pokazano po prawej.

Obwód bramki XNOR można wykonać z czterech bramek NOR. W rzeczywistości zarówno bramki NAND, jak i NOR są tak zwanymi „bramkami uniwersalnymi”, a każdą funkcję logiczną można zbudować z samej logiki NAND lub samej logiki NOR . Jeśli cztery bramki NOR zostaną zastąpione bramkami NAND, powstanie bramka XOR, którą można przekształcić w bramkę XNOR poprzez odwrócenie wyjścia lub jednego z wejść (np. za pomocą piątej bramki NAND).

Wymarzona brama	Konstrukcja NAND	Konstrukcja NOR

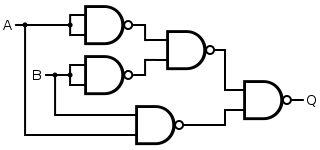
Alternatywnym układem jest pięć bramek NAND w topologii, która kładzie nacisk na konstrukcję funkcji od ${\ Displaystyle (A \ cdot B) + ({\ overline {A}} \cdot {\overline {B}})}$ , zauważając z prawa de Morgana , że bramka NAND jest bramką OR z odwróconym wejściem. Innym alternatywnym układem jest pięć bramek NOR w topologii, która kładzie nacisk na konstrukcję funkcji z ${\ Displaystyle (A + {\ overline {B}}) \ cdot ({\ overline {A}} + B)}$ , zauważając na podstawie prawa de Morgana , że bramka NOR jest wejściem odwróconym ORAZ brama.

Wymarzona brama	Konstrukcja NAND	Konstrukcja NOR

W przypadku konstrukcji NAND niższy układ oferuje zaletę krótszego opóźnienia propagacji (opóźnienie czasowe między zmianą wejścia a zmianą wyjścia). W przypadku konstrukcji NOR górny układ wymaga mniejszej liczby bramek.

Z przeciwnej perspektywy konstruowanie innych bramek przy użyciu tylko bramek XNOR jest możliwe, chociaż XNOR nie jest w pełni uniwersalną bramką logiczną . W ten sposób można zbudować bramki NOT i XOR.

Więcej niż dwa wejścia

Chociaż inne bramki (OR, NOR, AND, NAND) są dostępne u producentów z trzema lub więcej wejściami na bramkę, nie jest to do końca prawdziwe w przypadku bramek XOR i XNOR. Jednak rozszerzając koncepcję binarnej operacji logicznej na trzy wejścia, SN74S135 z dwoma współdzielonymi wejściami „C” i czterema niezależnymi wejściami „A” i „B” dla swoich czterech wyjść był urządzeniem zgodnym z tabelą prawdy:

Wejście			Wyjście
A	B	C	Y
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Jest to faktycznie Y = NIE ((A XOR B) XOR C). Innym sposobem interpretacji jest to, że dane wyjściowe są prawdziwe, jeśli parzysta liczba danych wejściowych jest prawdziwa. Nie implementuje logicznej funkcji „równoważności”, w przeciwieństwie do dwuwejściowych bramek XNOR.

Dodatkowo funkcja XOR wydaje się działać jako funkcja parzystości lub Mod2 dla sumy wszystkich danych wejściowych. Zauważ, że *y* jest równe 1, jeśli suma wszystkich danych wejściowych jest parzysta, co oznacza, że y = 0, jeśli suma wszystkich danych wejściowych jest nieparzysta. Możemy z tego wywnioskować, że x XOR y XOR z = jest parzyste (x+y+z).

Zobacz też

^ „Wyłączny samouczek bramki NOR” . Źródło 6 maja 2018 r .
^ „Bramki logiczne XNOR” . Źródło 6 maja 2018 r .

Linki zewnętrzne

[:0-1] „Wyłączny samouczek bramki NOR” . Źródło 6 maja 2018 r .

[2] „Bramki logiczne XNOR” . Źródło 6 maja 2018 r .

Spójniki logiczne
Tautologia / Prawda ${\ Displaystyle \ top}$
Alternatywna odmowa ( bramka NAND ) ${\ displaystyle \ uparrow}$ implikacja odwrotna ${\ displaystyle \ lefttarrow}$ Implikacja ( bramka IMPLY ) ${\ displaystyle \ rightarrow}$ Dysjunkcja ( bramka OR ) ${\ Displaystyle \ lor}$
Negacja ( bramka NOT ) ${\ Displaystyle \ neg}$ Wyłącznie lub ( bramka XOR ) ${\ Displaystyle \ nie \ leftrightarrow}$ Dwuwarunkowe ( bramka XNOR ) ${\ Displaystyle \ leftrightarrow}$ Wyciąg ( bufor cyfrowy )
Wspólne zaprzeczenie ( brama NOR ) ${\ Displaystyle \ downarrow}$ Brak implikacji ( bramka NIMPLY ) ${\ Displaystyle \ nrightarrow}$ Converse nonimplikacja ${\ Displaystyle \ nleftarrow}$ koniunkcja ( bramka AND ) ${\ displaystyle \ land}$
Sprzeczność / Fałsz ${\ displaystyle \ bot}$
Portal filozoficzny