Maska prostokątna z krótkotrwałą transformatą Fouriera

W matematyce i analizie Fouriera prostokątna maska ​​​​krótkotrwała transformata Fouriera (rec-STFT) ma prostą postać krótkotrwałej transformaty Fouriera . Inne typy STFT mogą wymagać więcej czasu obliczeniowego niż rec-STFT.

Prostokątną funkcję maski można zdefiniować dla pewnego ograniczenia ( B ) w czasie ( t ) jako

${\ Displaystyle w (t) = {\ rozpocząć {przypadki} \ 1; & | t | \ równoważnik B \\\ 0; & | t |> B \ koniec {przypadków}}}$

B = 50, oś x (s)

Możemy zmienić B dla różnych kompromisów między pożądaną rozdzielczością czasową a rozdzielczością częstotliwościową.

Rec-STFT

${\ Displaystyle X (t, f) = \ int _ {tB} ^ {t + B} x (\tau )e^{-j2\pi f\tau }\,d\tau }$

Forma odwrotna

${\ Displaystyle x (t) = \ int _ {- \ infty }^{\infty }X(t_{1},f)e^{j2\pi ft}\,df{\text{ gdzie }}tB<t_{1}<t+B}$

Nieruchomość

Rec-STFT ma podobne właściwości jak transformata Fouriera

• Integracja

(A)

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} X (t, f) \, df = \ int _ {tB} ^ {t + B} x (\ tau) \ int _ {- \ infty }^{\infty }e^{-j2\pi f\tau }\,df\,d\tau =\int _{tB}^{t+B}x(\tau )\delta (\tau ) \,d\tau ={\begin{przypadki}\ x(0);&|t|<B\\\ 0;&{\text{inaczej}}\end{przypadki}}}$

(B)

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} X (t, f) e ^ {- j2 \ pi fv} \, df = {\ rozpocząć {przypadki} \ x (v); & v- B<t<v+B\\\ 0;&{\text{inaczej}}\end{przypadki}}}$

• Właściwość przesuwania (przesunięcie wzdłuż osi x)

${\ Displaystyle \ int _{tB}^{t+B}x(\tau +\tau _{0})e^{-j2\pi f\tau }\,d\tau =X(t+\tau _{0}, f)e^{j2\pi f\tau _{0}}}$

• Właściwość modulacji (przesunięcie wzdłuż osi y )

${\ Displaystyle \ int _ {tB} ^ { t+B}[x(\tau )e^{j2\pi f_{0}\tau }]d\tau =X(t,f-f_{0})} specjalne$

• wejście

1. Gdy ${\ Displaystyle x (t) = \ delta (t), X (t, f) = {\ rozpocząć {przypadki} \ 1; & | t | <B \\\ 0; & {\ tekst {inaczej}} \end{przypadki}}}$
2. Kiedy ${\ Displaystyle x (t) = 1, X (t, f) = 2B \ nazwa operatora {sinc} (2Bf)e^{j2\pi stopa}}$

• Właściwość liniowości

Jeśli ${\ Displaystyle h (t) = \ alfa x (t) + \ beta y (t) \,}$ , ${\ Displaystyle H (t, f), X (t, f)}$ i ${\ Displaystyle Y (t, f) \}$ są ich rec-STFT, a następnie

${\ Displaystyle H (t, f) = \ alfa X (t, f) + \ beta Y (t, f).}$

• Właściwość integracji mocy

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} | X (t, f) | ^ {2} \, df = \ int _ {tB} ^ {t + B} | x ( \tau )|^{2}\,d\tau }$

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} | X (t, f) | ^ {2} \, df \, dt = 2B \int _{-\infty }^{\infty }|x(\tau )|^{2}\,d\tau }$

• Właściwość sumy energii ( Twierdzenie Parsevala )

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} X (t, f) Y ^ {*} (t, f) \, df = \ int _ {tB} ^ {t + B } x(\tau )y^{*}(\tau )\,d\tau }$

${\ Displaystyle \ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} X (t, f) Y ^ {*} (t, f) \, df \,dt=2B\int _{-\infty }^{\infty }x(\tau )y^{*}(\tau )\,d\tau }$

Przykład kompromisu z różnymi B

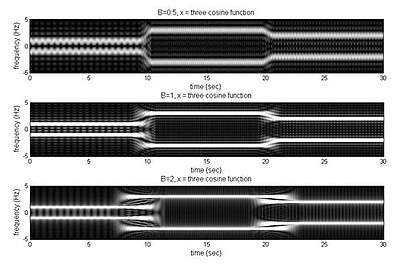
Spektrogramy utworzone przez zastosowanie rec-STFT na funkcji składającej się z 3 kolejnych fal cosinusoidalnych. (górny spektrogram używa mniejszego B równego 0,5, środkowy używa B równego 1, a dolny używa większego B równego 2.)

Z obrazu, gdy B jest mniejsze, rozdzielczość czasowa jest lepsza. W przeciwnym razie, gdy B jest większe, rozdzielczość częstotliwości jest lepsza.

Zaleta i wada

W porównaniu z transformatą Fouriera:

• Zaleta: można zaobserwować chwilową częstotliwość.
• Wada: Większa złożoność obliczeń.

W porównaniu z innymi rodzajami analizy czasowo-częstotliwościowej :

• Zaleta: Najkrótszy czas obliczeń dla implementacji cyfrowej.
• Wada: Jakość jest gorsza niż w przypadku innych rodzajów analizy czasowo-częstotliwościowej. Nieciągłość skokowa krawędzi prostokątnej maski powoduje artefakty dzwonienia Gibbsa w dziedzinie częstotliwości, które można złagodzić za pomocą gładszych okien .

Zobacz też

• Zasada niepewności

1. Jian-Jiun Ding (2014) Analiza czasowo-częstotliwościowa i transformacja falkowa