Metoda środkowego kwadratu

Jedna iteracja metody środkowych kwadratów, pokazująca 6-cyfrowe ziarno, które jest następnie podnoszone do kwadratu, a wynikowa wartość ma swoje 6 środkowych cyfr jako wartość wyjściową (a także jako następne ziarno w sekwencji).
Wykres skierowany wszystkich 100 2-cyfrowych liczb pseudolosowych uzyskanych metodą środkowych kwadratów przy n = 2.

W matematyce i informatyce metoda środkowych kwadratów jest metodą generowania liczb pseudolosowych . W praktyce jest to metoda wysoce wadliwa z wielu praktycznych powodów, ponieważ jej okres jest zwykle bardzo krótki i ma kilka poważnych słabości; powtarzane wystarczająco dużo razy, metoda środkowego kwadratu albo zacznie wielokrotnie generować tę samą liczbę, albo przejdzie do poprzedniej liczby w sekwencji i zapętli się w nieskończoność.

Historia

W matematyce

Metoda została wynaleziona przez Johna von Neumanna i została przez niego opisana na konferencji w 1949 roku.

W przemówieniu z 1949 roku Von Neumann zażartował, że „Każdy, kto rozważa arytmetyczne metody tworzenia losowych cyfr, jest oczywiście w stanie grzechu”. Wyjaśnił, że miał na myśli to, że nie było prawdziwych „liczb losowych”, tylko sposoby ich tworzenia, a „ścisła procedura arytmetyczna”, taka jak metoda środkowego kwadratu, „nie jest taką metodą”. Niemniej jednak odkrył, że te metody są setki razy szybsze niż czytanie „prawdziwie” losowych liczb z kart perforowanych , co miało praktyczne znaczenie dla jego ENIAC praca. Uznał, że „zniszczenie” sekwencji środkowych kwadratów działa na ich korzyść, ponieważ można je łatwo wykryć: „zawsze obawia się pojawienia się niewykrytych krótkich cykli”. Nicholas Metropolis zgłosił sekwencje 750 000 cyfr przed „zniszczeniem” za pomocą liczb 38-bitowych metodą „środkowego kwadratu”.

Książka The Broken Dice autorstwa Ivara Ekelanda zawiera obszerny opis tego, jak metoda została wynaleziona przez franciszkanina znanego tylko jako brat Edvin, gdzieś między 1240 a 1250 rokiem. Podobno rękopis zaginął, ale Jorge Luis Borges wysłał Ekelandowi kopię, która dokonał w Bibliotece Watykańskiej.

Modyfikacja algorytmu środkowego kwadratu za pomocą sekwencji Weyla poprawia okres i losowość.

Metoda

Aby wygenerować sekwencję n -cyfrowych liczb pseudolosowych, tworzona jest n -cyfrowa wartość początkowa i podnoszona do kwadratu, co daje 2 n -cyfrową liczbę. Jeśli wynik ma mniej niż 2 n cyfr, w celu skompensowania dodawane są wiodące zera . Środkowe n cyfr wyniku będzie następną liczbą w sekwencji i zwrócone jako wynik. Ten proces jest następnie powtarzany, aby wygenerować więcej liczb.

Wartość n musi być parzysta, aby metoda działała – jeśli wartość n jest nieparzysta, niekoniecznie będzie istniała jednoznacznie zdefiniowana „środkowa liczba n ” do wyboru. Weź pod uwagę następujące kwestie: Jeśli 3-cyfrowa liczba zostanie podniesiona do kwadratu, może dać liczbę 6-cyfrową (np. 540 2 = 291600). Gdyby były 3 środkowe cyfry, pozostawiłoby to 6 - 3 = 3 cyfry do rozmieszczenia po lewej i prawej stronie środka. Niemożliwe jest równomierne rozłożenie tych cyfr po obu stronach liczby środkowej, dlatego nie ma „cyfr środkowych”. Dopuszczalne jest dostawianie nasion zerami z lewej strony w celu utworzenia n -cyfrowej liczby parzystej (np. 540 → 0540).

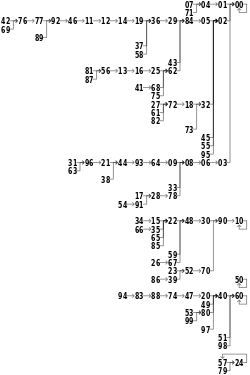
Dla generatora liczb n -cyfrowych okres nie może być dłuższy niż 8 n . Jeśli środkowe n cyfr to wszystkie zera, generator wyprowadza zera na zawsze. Jeśli pierwsza połowa liczby w sekwencji to zera, kolejne liczby będą maleć do zera. Chociaż te przebiegi zerowe są łatwe do wykrycia, występują zbyt często, aby ta metoda była praktyczna. Metoda środkowego kwadratu może również utknąć na liczbie innej niż zero. dla n = 4, dzieje się tak z wartościami 0100, 2500, 3792 i 7600. Inne wartości początkowe tworzą bardzo krótkie powtarzające się cykle, np. 0540 → 2916 → 5030 → 3009. Zjawiska te są jeszcze bardziej oczywiste, gdy n = 2, ponieważ żadne z 100 możliwych nasion generuje więcej niż 14 iteracji bez powrotu do pętli 0, 10, 50, 60 lub 24 ↔ 57.

Przykładowa realizacja

Tutaj algorytm jest renderowany w Pythonie 3 . 

  
  
  
  0

    
      
    
       numer_ziarna  =  int  (  input  (  „Proszę wprowadzić czterocyfrową liczbę:  \n  [####] "  ))  number  =  numer_ziarnowy  już_widziany  =  set  ()  licznik  =  podczas gdy  liczba  nie  jest  już widziana  :  licznik  +=  1  już_widziany  .  dodaj  (  liczba  )  liczba  =  int  (  str  (  liczba     
    


      
       *  numer  )  .  zfill  (  8  )[  2  :  6  ])  # zfill dodaje dopełnienie zer  print  (  f  "#  {  licznik  }  :  {  liczba  }  "  )  print  (  f  "Zaczęliśmy od  {  numer_ziarna  }  i"  f  " powtórzyliśmy się po  {  licznik  }  kroki”  f  " z  {  liczba  }  ".  )
  1. ^ a b Artykuły z 1949 r. Przedrukowano dopiero w 1951 r. John von Neumann, „Różne techniki stosowane w połączeniu z losowymi cyframi”, w AS Householder, GE Forsythe i HH Germond, red., Monte Carlo Method, National Bureau of Standards Applied Seria matematyczna , tom. 12 (Waszyngton, DC: US ​​Government Printing Office, 1951): s. 36–38.
  2. ^ Donald E. Knuth, Sztuka programowania komputerowego, tom. 2, Algorytmy półnumeryczne , wyd. 2. (Reading, Mass.: Addison-Wesley, 1981), rozdz. 3 ust. 3.1.
  3. ^   Ivar Ekeland (15 czerwca 1996). Złamane kości i inne matematyczne opowieści o przypadku . Wydawnictwo Uniwersytetu Chicagowskiego. ISBN 978-0-226-19992-4 .
  4. ^ Kneusel, Ron (2018). Liczby losowe i komputery (1 wyd.). Skoczek. s. 13–14.
  5. ^ Widyński, Bernard (kwiecień 2017). „RNG sekwencji Weyla środkowego kwadratu” . arXiv : 1704.00358 [ cs.CR ].

Zobacz też

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Middle-square_method&oldid=1133526771 ”