Model Goodwina (ekonomia)

Model Goodwina , czasami nazywany modelem walki klasowej Goodwina , jest modelem endogenicznych fluktuacji ekonomicznych, zaproponowanym po raz pierwszy przez amerykańskiego ekonomistę Richarda M. Goodwina w 1967 roku. Łączy w sobie aspekty modelu wzrostu Harroda-Domara z krzywą Phillipsa do generowania endogenicznych cykli aktywności gospodarczej (produkcja, bezrobocie i płace) w przeciwieństwie do większości współczesnych modeli makroekonomicznych, w których zmiany agregatów ekonomicznych są napędzane przez egzogenicznie zakładane szoki. Od czasu publikacji Goodwina w 1967 roku model ten był rozszerzany i stosowany na różne sposoby.

Model

Model opiera się na następujących założeniach:

następuje stały wzrost wydajności pracy (np. poprzez postęp technologiczny);
następuje stały wzrost siły roboczej (np. poprzez urodzeń);
są tylko dwa czynniki produkcji: praca i kapitał;
robotnicy całkowicie konsumują swoje płace, a kapitaliści całkowicie inwestują swoje zyski;
stosunek produkcji kapitału do produkcji jest stały (tj. ustalona wielkość produkcji zawsze może zostać przekształcona w tę samą ilość kapitału);
płace realne zmieniają się zgodnie z linearyzowaną krzywą Phillipsa , gdzie płace rosną, gdy są bliskie pełnego zatrudnienia.

Model wykorzystuje zmienne

q to produkcja

k to (jednorodny) kapitał

w to stawka płac

a to produktywność pracy

n to siła robocza

które są wszystkimi funkcjami czasu (chociaż dla wygody indeksy czasowe zostały usunięte) i stałymi

α to stopa wzrostu wydajności pracy

β to stopa wzrostu siły roboczej

γ służy do zdefiniowania krzywej zmian płac realnych

ρ jest również używana do zdefiniowania krzywej zmian płac realnych

σ to stosunek kapitału do produkcji.

Szereg wielkości pochodnych jest pomocnych w zdefiniowaniu modelu. Ilość zatrudnionej siły roboczej jest określona przez

{\ Displaystyle l = {\ Frac {q} {a}}}

,

stosunek zatrudnienia jest określony przez

{\ Displaystyle v = {\ Frac {l} {n}}}

,

pracowników w produkcji jest określony przez

{\ Displaystyle u = {\ Frac {wl} {q}} = {\ Frac {w} {a}}}

,

a udział kapitalistów w produkcji ( dla nadwyżki) jest określony przez ${\ displaystyle s}$

{\ displaystyle s = 1-u}

.

Model jest następnie definiowany za pomocą zestawu równań różniczkowych. Po pierwsze, zmiana wydajności pracy jest określona przez

{\ Displaystyle {\ Frac {\ kropka {a}} {a}} = \ alfa}

,

to znaczy stały wzrost, z za ${\ Displaystyle a_ {t} = a_ {0} e ^ {\ alfa t$ . (Zauważ, że jest pochodną po czasie ${dx} / {dt}}$ ${\ Displaystyle$ .) Siła robocza zmienia się zgodnie z x ˙ {

{\ Displaystyle {\ Frac {\ kropka {n}} {n}} = \ beta}

,

znowu stały wzrost, z ${\ displaystyle n_ {t} = n_ {0} e ^ {\ beta t}}$ . Płace realne zmieniają się wg

{\ Displaystyle {\ Frac {\ kropka {w}} {w}} = - \ gamma + \ rho v}

,

to znaczy krzywa zmiany płac realnych jest modelowana jako liniowa. Zauważ, że aby poprawnie modelować założenia, należy wybrać i $\ rho},$ $displaystyle$ $aby zapewnić wzrost płac realnych,$ Innymi słowy, jeśli siła robocza rynek jest „ napięty ” (zatrudnienie jest już wysokie), istnieje presja na wzrost płac i odwrotnie na „luźnym” rynku pracy.

Zmiany kapitału wg

{\ Displaystyle {\ kropka {k}} = qs}

,

ponieważ zakłada się, że nadwyżka jest całkowicie inwestowana przez kapitalistę. Wreszcie, dane wyjściowe zmieniają się zgodnie z

{\ Displaystyle {\ Frac {\ kropka {q}}} {q}} = {\ Frac {s} {\ sigma}}}

,

to znaczy proporcjonalnie do zainwestowanej nadwyżki.

Zauważ to

{\ Displaystyle {\ Frac {\ kropka {q}} {q}} = {\ Frac {\ kropka {k}} {k}} = {\ Frac {1 -u {\sigma }}}

przy założeniu, że k i q rosną w tym samym tempie przy założeniu pełnego wykorzystania kapitału i stałych korzyści skali.

Rozwiązanie

Równania definiujące można rozwiązać dla ${\ kropka {v}}}$ v $\ Displaystyle$ , co daje dwa równania

{\ Displaystyle {\ kropka {v}} = v (- {\ Frac {1} {\ sigma}} u + {\ Frac {1} \ sigma}} - \ alfa - \ beta)}

{\ Displaystyle {\ kropka {u}} = u (\ rho v- \ gamma - \ alfa)}

.

Są to kluczowe równania modelu iw rzeczywistości są to równania Lotki-Volterry , które są używane w biologii do modelowania interakcji drapieżnik-ofiara. Równania te mają dwa punkty stałe. Pierwszy to kiedy

{\ displaystyle u = 0}

i

{\ displaystyle v = 0}

a drugi to kiedy

{\ Displaystyle u = 1- (\ alfa + \ beta) \ sigma}

{\ Displaystyle v = {\ Frac {\ gamma + \ alfa} {\ rho }}}

,

który określa środek rodziny trajektorii cyklicznych.

Ponieważ model nie może być rozwiązany jawnie, pouczająca jest analiza trajektorii gospodarki w kategoriach diagramu fazowego . Dwie linie wyznaczające środek cyklu dzielą dodatni ortan na cztery regiony. Poniższy rysunek wskazuje strzałkami ruch gospodarczy w każdym regionie. Na przykład w regionie północno-zachodnim (wysokie zatrudnienie, niski udział pracy w produkcji) gospodarka przesuwa się na północny wschód (zatrudnienie rośnie, udział pracowników rośnie). Po przekroczeniu linii u* zacznie poruszać się w kierunku południowo-zachodnim.

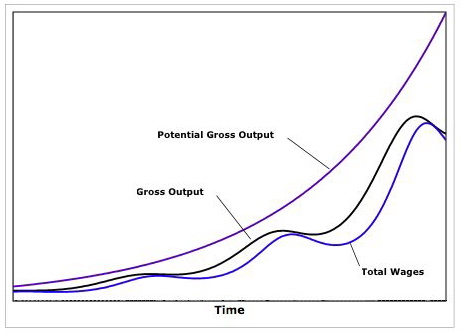
Poniższy rysunek ilustruje ruch potencjalnej produkcji (produkcji przy pełnym zatrudnieniu), rzeczywistej produkcji i płac w czasie.

Jak widać, model Goodwina może generować endogeniczne fluktuacje aktywności gospodarczej bez polegania na zewnętrznych założeniach szoków zewnętrznych, czy to po stronie popytu, czy podaży.

Statystyka

Udział płac (niebieska linia) i wskaźnik ludności cywilnej zatrudnionej (czerwona linia) w Stanach Zjednoczonych Zgodnie z modelem Goodwina należy oczekiwać, że udział płac będzie opóźniony w stosunku do wskaźnika zatrudnienia. Wydaje się, że dzieje się tak choćby z niewielkim opóźnieniem czasowym

Zobacz też

Notatki

Goodwin, Richard M. (1967), „Cykl wzrostu”, w CH Feinstein, redaktor, Socjalizm, kapitalizm i wzrost gospodarczy . Cambridge: Cambridge University Press.
Goodwin, Richard M., Chaotyczna dynamika gospodarcza , Oxford University Press , 1990.
Flaschel, Peter, Makrodynamika kapitalizmu - elementy syntezy Marksa, Keynesa i Schumpetera. Wydanie drugie, Springer Verlag Berlin 2010. Rozdział 4.3.