Najniższy wspólny przodek

Ten artykuł dotyczy najniższych wspólnych przodków w teorii grafów i informatyce. Aby zapoznać się ze wspólnym przodkiem zestawu gatunków w drzewach ewolucyjnych, zobacz najnowszy wspólny przodek . Aby zapoznać się ze wspólnym przodkiem wszystkich form życia, zobacz ostatni uniwersalny wspólny przodek .

kolorem ciemnozielonym zaznaczony jest najniższy wspólny przodek węzłów x i y . Inni wspólni przodkowie są pokazani w kolorze jasnozielonym.

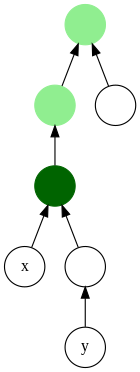
W teorii grafów i informatyce najniższy wspólny przodek ( LCA ) (zwany także najmniejszym wspólnym przodkiem) dwóch węzłów v i w w drzewie lub skierowanym grafie acyklicznym (DAG) T jest najniższym (tj. najgłębszym) węzłem, który ma oba v i w jako potomkowie, gdzie definiujemy każdy węzeł jako potomka samego siebie (więc jeśli v ma bezpośrednie połączenie z w , w jest najniższym wspólnym przodkiem).

LCA v i w w T jest wspólnym przodkiem v i w , który znajduje się najdalej od korzenia. Obliczenie najniższych wspólnych przodków może być przydatne na przykład jako część procedury określania odległości między parami węzłów w drzewie: odległość od v do w można obliczyć jako odległość od korzenia do v powiększoną o odległość od korzenia do w minus dwukrotna odległość od korzenia do ich najniższego wspólnego przodka ( Djidżew, Pantziou i Zaroliagis 1991 ). W ontologiach najniższy wspólny przodek jest również znany jako najmniej wspólny przodek .

W drzewiastej strukturze danych , w której każdy węzeł wskazuje na swojego rodzica, najniższego wspólnego przodka można łatwo określić, znajdując pierwsze przecięcie ścieżek od v i w do korzenia. Ogólnie czas obliczeń wymagany dla tego algorytmu wynosi O(h) , gdzie h to wysokość drzewa (długość najdłuższej ścieżki od liścia do korzenia). Istnieje jednak kilka algorytmów przetwarzania drzew, dzięki którym można szybciej znaleźć najniższych wspólnych przodków. Algorytm najniższego wspólnego przodka Tarjana offline , na przykład, wstępnie przetwarza drzewo w czasie liniowym, aby zapewnić zapytania LCA o stałym czasie. Ogólnie rzecz biorąc, istnieją podobne algorytmy DAG, ale o złożoności superliniowej.

Historia

Problem najniższego wspólnego przodka został zdefiniowany przez Alfreda Aho , Johna Hopcrofta i Jeffreya Ullmana ( 1973 ), ale Dov Harel i Robert Tarjan ( 1984 ) jako pierwsi opracowali optymalnie wydajną strukturę danych najniższego wspólnego przodka. Ich algorytm przetwarza dowolne drzewo w czasie liniowym, stosując dekompozycję ciężkich ścieżek , dzięki czemu na kolejne zapytania o najniższych wspólnych przodkach można odpowiadać w stałym czasie na zapytanie. Jednak ich struktura danych jest złożona i trudna do wdrożenia. Tarjan znalazł również prostszy, ale mniej wydajny algorytm, oparty na struktura danych znajdowania związków , do obliczania najniższych wspólnych przodków partii offline par węzłów .

Baruch Schieber i Uzi Vishkin ( 1988 ) uprościli strukturę danych Harela i Tarjana, prowadząc do możliwej do wdrożenia struktury z tymi samymi asymptotycznymi ograniczeniami czasowymi przetwarzania wstępnego i zapytań. Ich uproszczenie opiera się na zasadzie, że w dwóch specjalnych rodzajach drzew łatwo jest określić najniższych wspólnych przodków: jeśli drzewo jest ścieżką, to najniższego wspólnego przodka można obliczyć po prostu na podstawie minimum poziomów dwóch zapytanych węzłów, podczas gdy drzewo jest kompletnym drzewem binarnym , węzły mogą być indeksowane w taki sposób, że najniżsi wspólni przodkowie redukują się do prostych operacji binarnych na indeksach. Struktura Schiebera i Vishkina rozkłada dowolne drzewo na zbiór ścieżek, tak że połączenia między ścieżkami mają strukturę drzewa binarnego i łączy obie te dwie prostsze techniki indeksowania.

Omer Berkman i Uzi Vishkin ( 1993 ) odkryli zupełnie nowy sposób odpowiadania na zapytania o najniższych wspólnych przodkach, ponownie uzyskując liniowy czas przetwarzania wstępnego przy stałym czasie zapytania. Ich metoda polega na utworzeniu trasy Eulera po grafie utworzonym z drzewa wejściowego przez podwojenie każdej krawędzi i użyciu tej trasy do zapisania sekwencji numerów poziomów węzłów w kolejności, w jakiej odwiedza je trasa; zapytanie o najniższego wspólnego przodka można następnie przekształcić w zapytanie, które szuka minimalnej wartości występującej w pewnym podprzedziale tej sekwencji liczb. Następnie obsługują to zapytanie o minimalny zakres problemu (RMQ) poprzez połączenie dwóch technik, jednej techniki opartej na wstępnym obliczaniu odpowiedzi dla dużych przedziałów, których rozmiary są potęgami dwójki, a drugiej opartej na przeszukiwaniu tabeli dla zapytań o małych przedziałach. Metoda ta została później przedstawiona w uproszczonej formie przez Michaela Bendera i Martina Farach-Coltona ( 2000 ). Jak zauważyli wcześniej Gabow, Bentley i Tarjan (1984) , problem minimalnego zasięgu można z kolei przekształcić z powrotem w problem najniższego wspólnego przodka przy użyciu techniki drzew kartezjańskich .

Dalszych uproszczeń dokonali Alstrup i in. (2004) oraz Fischera i Heuna (2006) .

Sleator i Tarjan ( 1983 ) zaproponowali dynamiczny wariant problemu LCA, w którym struktura danych powinna być przygotowana do obsługi zapytań LCA połączonych z operacjami zmieniającymi drzewo (tj. przestawianie drzewa poprzez dodawanie i usuwanie krawędzi). Ten wariant można rozwiązać w $rozmiarze$ drzewa dla wszystkich Odbywa się to poprzez utrzymywanie lasu przy użyciu dynamicznej struktury danych drzew z partycjonowaniem według rozmiaru; to następnie utrzymuje rozkład ciężki-lekki każdego drzewa i umożliwia przeprowadzanie zapytań LCA w czasie logarytmicznym w rozmiarze drzewa.

Przestrzeń liniowa i stały czas wyszukiwania rozwiązanie problemu LCA opartego na drzewie

Jak wspomniano powyżej, LCA można najpierw zredukować do RMQ, a następnie podzielić sekwencję liczb na przedziały i zastosować dwie różne techniki do obsługi zapytania o minimalny zakres w różnych przedziałach oraz do obsługi zapytania o minimalny zakres w przedziale.

Redukcja z LCA do RMQ

Redukcja LCA do RMQ rozpoczęła się od chodzenia po drzewie. Podczas chodzenia po drzewie rejestrowana jest kolejność etykiet i głębokość odwiedzanego węzła. Następnie można odpowiedzieć na pytanie LCA, odpowiadając na pytanie RMQ, którego wejściem problemu RMQ są indeksy dwóch węzłów potomnych na liście odwiedzonych węzłów.

Przykład pokazuje, jak RMQ jest redukowane do LCA.

Dlatego LCA można rozwiązać, rozwiązując RMQ.

Algorytm liniowej przestrzeni i stałego czasu wyszukiwania dla RMQ zredukowany z LCA

Mimo to istnieje stałe rozwiązanie w czasie i przestrzeni liniowej dla ogólnego RMQ, ale można zastosować uproszczone rozwiązanie, które wykorzystuje właściwości LCA. To uproszczone rozwiązanie może być stosowane tylko w przypadku RMQ zredukowanego z LCA.

$,$ do rozwiązania wspomnianego powyżej, dzielimy sekwencję na każdy blok $\ styl wyświetlania b={1 \ponad 2}\log n}$ blok $ma$ rozmiar .

Ilustracja przedstawiająca problem RMQ jest podzielona na bloki, z których każdy ma rozmiar = b

Dzieląc sekwencję na bloki, zapytanie można rozwiązać, rozwiązując dwa różne przypadki: ${\ Displaystyle RMQ (i, j)}$

Przypadek 1: jeśli i i j są w różnych blokach

Aby odpowiedzieć na $.$ w pierwszym przypadku, istnieją 3 grupy zmiennych

$Po$ pierwsze, minimalny element z najmniejszym indeksem w każdym bloku jest wstępnie obliczany i oznaczany jako $y_ {i}}$ . Zbiór zajmuje miejsce ${\ Displaystyle O (n/b$$)$

Po drugie, biorąc pod uwagę zbiór , zapytanie RMQ dla tego zestawu jest wstępnie obliczane przy użyciu $rozwiązania$ ze stałym czasem i przestrzenią liniowo - Istnieją bloki ${\ Displaystyle n/b}$ , więc tabela odnośników w tym rozwiązaniu zajmuje ${\ Displaystyle O ({n \ ponad b} \ log {n \ ponad b} )}$ spacja. Ponieważ ${\ Displaystyle b = {1 \ ponad 2} \ log n}$ , ${\ Displaystyle O ({n \ ponad b} \ log {n \ ponad b})}$ = $_$ . $wstępnie$ zapytanie RMQ wykorzystujące ze stałym czasem i przestrzenią liniowo-arytmiczną tych blokach zajmuje tylko miejsce.

$} styl wyświetlania 0\równoważnik ki<b}$ każdym bloku niech $Displaystyle B_$ indeksem w $\$ , że $≤$ . Dla wszystkich $\ Displaystyle$ { $0}$ do ${\ Displaystyle b}$ blok jest $\ Displaystyle B_ {i}}$ dwa przedziały k ja ${\ Displaystyle [0, k_ {i}}} i$ [ $\ Displaystyle [k_ {i}, b)}$ . Następnie minimalny element $}$ najmniejszym indeksie dla przedziałów każdym bloku b $Displaystyle$${\ Displaystyle B_ {i}}$ jest wstępnie obliczony. Takie minimalne elementy nazywane są przedrostkiem min dla przedziału w ${\ Displaystyle [0, k_ {i}}}$ i przyrostkiem min dla przedziału w ${\ Displaystyle [k_ {i}} ,b)}$ . Każda iteracja $oblicza$ parę przedrostków min i sufiksów $wynosi$ całkowita liczba minut przedrostka i minut sufiksu b ${\ Displaystyle 2b}$ . Ponieważ istnieją $bloki$ , w sumie wszystkie tablice min przedrostków i sufiksów min zajmują $)}$ czyli przestrzenie ${\ Displaystyle O (n)}$ .

W sumie zajmuje miejsce do $obliczonych zmiennych$ powyżej.

Dlatego udzielenie odpowiedzi na zapytanie w przypadku 1 to po prostu zadanie minimum z następujących trzech pytań: ${\ displaystyle RMQ (i, j)}$

Niech ${\ displaystyle B_ {i}}$ będzie blokiem zawierającym element w indeksie $displaystyle$$B_ {j}}$ jo {\ dla indeksu $\ displaystyle j}$ .

1. Sufiks min w ${\ Displaystyle [i \ mod b, b)}$ w bloku ${\ Displaystyle B_ {i}}$
2. ${\ Displaystyle \ {B_ {i + 1}... B_ {j-1} \}}$ RMQ na podzbiorze ${$ z bloków przy użyciu rozwiązania o stałym czasie i przestrzeni liniowo-arytmicznej
3. Przedrostek min w ${\ Displaystyle [0, j \ mod b)}$ w bloku ${\ Displaystyle B_ {j}}$

Na wszystkie 3 pytania można odpowiedzieć w stałym czasie. Stąd przypadek 1 można rozwiązać w przestrzeni liniowej i stałym czasie.

Przypadek 2: jeśli i i j są w tym samym bloku

Sekwencja RMQ, która została zredukowana z LCA, ma jedną właściwość, której nie ma normalny RMQ. Następny element to zawsze +1 lub -1 od bieżącego elementu. Na przykład:

Ilustracja pokazująca, jak przykładowy RMQ jest zakodowany jako ciąg bitów

Dlatego każdy blok $.$ zakodować jako ciąg bitów, w którym 0 reprezentuje bieżącą głębokość -1, a 1 reprezentuje bieżącą głębokość Ta transformacja zamienia blok $displaystyle b-$ łańcuch bitów o rozmiarze $ja {$ . Łańcuch bitów o rozmiarze ma $Displaystyle 2 ^ {b-1}}$$\$ bitów Ponieważ ${\ Displaystyle b = {1 \ ponad 2} \ log n}$ , więc ${\ Displaystyle 2 ^ {b- 1}\leq 2^{b}=2^{{1 \over 2}\log n}=n^{1 \over 2}={\sqrt {n}}}$ .

Dlatego $jest$ zawsze jednym z możliwych $.$ bitów o rozmiarze $b-1}$ \

Następnie dla każdego możliwego łańcucha bitów stosujemy naiwne kwadratowe rozwiązanie ze stałą przestrzenną w czasie . ${\ Displaystyle O ({\ sqrt {n}} \ cdot (\ log n) ^ {2}) \ równoważnik O ({\ sqrt {n}} \ cdot {\ sqrt {n}}) = O (n)}$ zajmie czyli $_$ .

Dlatego udzielenie odpowiedzi na $.$ w przypadku 2 polega po prostu na znalezieniu odpowiedniego bloku (w którym znajduje się ciąg bitów) Stąd przypadek 2 można rozwiązać za pomocą przestrzeni liniowej ze stałym czasem wyszukiwania.

Rozszerzenie do skierowanych grafów acyklicznych

DAG ze wspólnymi przodkami x i y w kolorze jasnozielonym i ich najniższymi wspólnymi przodkami w kolorze ciemnozielonym.

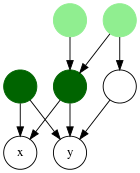
Chociaż pierwotnie badano w kontekście drzew, pojęcie najniższych wspólnych przodków można zdefiniować dla skierowanych grafów acyklicznych (DAG), używając jednej z dwóch możliwych definicji. W obu zakłada się, że krawędzie DAG wskazują od rodziców do dzieci.

• Biorąc pod uwagę G = ( V , E ) , Aït-Kaci i in. (1989) zdefiniują poset ( V , ≤) taki, że x ≤ y iff x jest osiągalny z y . Najniżsi wspólni przodkowie x i y są zatem minimalnymi elementami pod ≤ zbioru wspólnego przodka { z ∈ V | x ≤ z i y ≤ z }.
• Bender i in. (2005) , w której najniższymi wspólnymi przodkami x i y są węzły poza stopniem zerowym w podgrafie G indukowanym przez zbiór wspólnych przodków x i y .

Na drzewie najniższy wspólny przodek jest wyjątkowy; w DAG o n węzłach każda para węzłów może mieć aż n -2 LCA ( Bender et al. 2005 ), podczas gdy istnienie LCA dla pary węzłów nie jest nawet gwarantowane w dowolnie połączonych DAG.

Algorytm brutalnej siły służący do znajdowania najniższych wspólnych przodków został podany przez Aït-Kaci i in. (1989) : znajdź wszystkich przodków x i y , a następnie zwróć maksymalny element przecięcia dwóch zbiorów. Istnieją lepsze algorytmy, które analogicznie do algorytmów LCA na drzewach wstępnie przetwarzają graf, aby umożliwić zapytania LCA w stałym czasie. Problem istnienia LCA można optymalnie rozwiązać dla rzadkich DAG za pomocą algorytmu O(| V || E |) dzięki Kowaluk & Lingas (2005) .

Dash i in. (2013) przedstawiają ujednoliconą strukturę do wstępnego przetwarzania ukierunkowanych grafów acyklicznych w celu obliczenia reprezentatywnego najniższego wspólnego przodka w ukorzenionym DAG w stałym czasie. Ich ramy mogą osiągnąć prawie liniowe czasy przetwarzania wstępnego dla rzadkich wykresów i są dostępne do użytku publicznego.

Aplikacje

Problem obliczania najniższych wspólnych przodków klas w hierarchii dziedziczenia pojawia się przy implementacji systemów programowania obiektowego ( Aït-Kaci i in. 1989 ). Problem LCA znajduje również zastosowanie w modelach złożonych systemów występujących w przetwarzaniu rozproszonym ( Bender et al. 2005 ).

Zobacz też

• Problem z przodkiem poziomu
• Semikrata

•   Ach, Alfredzie ; Hopcroft, Jan ; Ullman, Jeffrey (1973), „O znalezieniu najniższych wspólnych przodków na drzewach”, Proc. 5. Symp. ACM. Teoria informatyki (STOC) , s. 253–265, doi : 10.1145/800125.804056 , S2CID 17705738 .
•    Aït-Kaci, H.; Boyer, R.; Lincoln, P.; Nasr, R. (1989), „Wydajna implementacja operacji kratowych” (PDF) , ACM Transactions on Programming Languages ​​and Systems , 11 (1): 115–146, CiteSeerX 10.1.1.106.4911 , doi : 10.1145/59287.59293 , S2CID 2931984 .
•    Alstrup, Stefan; Gavoille, Cyryl; Kaplan, Haim; Rauhe, Theis (2004), „Najbliżsi wspólni przodkowie: badanie i nowy algorytm dla środowiska rozproszonego” , Theory of Computing Systems , 37 (3): 441–456, CiteSeerX 10.1.1.76.5973 , doi : 10.1007/s00224 -004-1155-5 , S2CID 9447127 . Wstępna wersja ukazała się w SPAA 2002.
•   Bender, Michael A.; Farach-Colton, Martin (2000), „Powrót do problemu LCA”, Proceedings of the 4th Latin American Symposium on Theoretical Informatics , Lecture Notes in Computer Science , tom. 1776, Springer-Verlag, s. 88–94 , doi : 10.1007/10719839_9 , ISBN 978-3-540-67306-4 .
• Bender, Michael A.; Farach-Colton, Martin ; Pemmasani, Giridhar; Skiena, Steven ; Sumazin, Pavel (2005), „Najniżsi wspólni przodkowie drzew i skierowane grafy acykliczne” (PDF) , Journal of Algorithms , 57 (2): 75–94, doi : 10.1016/j.jalgor.2005.08.001 .
• Berkman, Omer; Vishkin, Uzi (1993), „Recursive Star-Tree Parallel Data Structure” , SIAM Journal on Computing , 22 (2): 221–242, doi : 10.1137/0222017 , zarchiwizowane z oryginału 23 września 2017 r .
• Dash, Santanu Kumar; Scholz, Sven-Bodo; Herhut, Stefan; Christianson, Bruce (2013), „Skalowalne podejście do obliczania reprezentatywnego najniższego wspólnego przodka w skierowanych grafach acyklicznych” (PDF) , Theoretical Computer Science , 513 : 25–37, doi : 10.1016/j.tcs.2013.09.030 , hdl : 2299/12152
•   Djidjev, Christo N.; Pantziou, Grammati E.; Zaroliagis, Christos D. (1991), „Obliczanie najkrótszych ścieżek i odległości na grafach planarnych”, Automaty, języki i programowanie: 18th International Colloquium, Madryt, Hiszpania, 8–12 lipca 1991, Proceedings , Lecture Notes in Computer Science, tom . 510, Springer, s. 327–338, doi : 10.1007/3-540-54233-7_145 , ISBN 978-3-540-54233-9 .
•    Fischer, Johannes; Heun, Volker (2006), „Teoretyczne i praktyczne ulepszenia problemu RMQ, z zastosowaniami do LCA i LCE”, Proceedings of the 17th Annual Symposium on Combinatoric Pattern Matching , Notatki z wykładów z informatyki, tom. 4009, Springer-Verlag, s. 36–48, CiteSeerX 10.1.1.64.5439 , doi : 10.1007/11780441_5 , ISBN 978-3-540-35455-0 .
•    Gabow, Harold N .; Bentley, Jon Louis ; Tarjan, Robert E. (1984), „Skalowanie i pokrewne techniki problemów geometrii”, STOC '84: Proc. 16 Sympozjum ACM na temat teorii informatyki , Nowy Jork, NY, USA: ACM, s. 135–143, doi : 10.1145/800057.808675 , ISBN 978-0897911337 , S2CID 17752833 .
• Harel, Dow; Tarjan, Robert E. (1984), „Szybkie algorytmy wyszukiwania najbliższych wspólnych przodków”, SIAM Journal on Computing , 13 (2): 338–355, doi : 10.1137/0213024 .
•    Kowaluk, Mirosław; Lingas, Andrzej (2005), „Zapytania LCA w skierowanych grafach acyklicznych”, w: Caires, Luís; Italiano, Giuseppe F .; Monteiro, Luís; Palamidessi, Catuscia; Yung, Moti (red.), Automaty, języki i programowanie, 32. Międzynarodowe Kolokwium, ICALP 2005, Lizbona, Portugalia, 11-15 lipca 2005, Proceedings , Lecture Notes in Computer Science, tom. 3580, Springer, s. 241–248 , CiteSeerX 10.1.1.460.6923 , doi : 10.1007/11523468_20 , ISBN 978-3-540-27580-0
• Schieber, Baruch ; Vishkin, Uzi (1988), „O znalezieniu najniższych wspólnych przodków: uproszczenie i zrównoleglenie”, SIAM Journal on Computing , 17 (6): 1253–1262, doi : 10.1137/0217079 .
•   Sleator, DD ; Tarjan, RE (1983), „Struktura danych dla drzew dynamicznych” (PDF) , Proceedings of the trzynasty doroczny sympozjum ACM na temat teorii obliczeń - STOC '81 , s. 114–122, doi : 10.1145 / 800076.802464 , S2CID 15402750

Linki zewnętrzne

• Najniższy wspólny przodek drzewa wyszukiwania binarnego , autor: Kamal Rawat
• Implementacja w języku Python algorytmu Bendera i Faracha-Coltona dla drzew autorstwa Davida Eppsteina
• Implementacja Pythona dla dowolnie skierowanych grafów acyklicznych
• Notatki z wykładów na temat LCA z kursu MIT Data Structures z 2003 roku . Kurs Erika Demaine'a , notatki napisane przez Loizosa Michaela i Christosa Kapoutsisa. Notatki z oferty tego samego kursu z 2007 roku , napisane przez Alison Cichowlas.
• Najniższy wspólny przodek w drzewach binarnych w C . Uproszczona wersja techniki Schiebera-Vishkina, która działa tylko w przypadku zrównoważonych drzew binarnych.
• Film przedstawiający Donalda Knutha wyjaśniającego technikę Schiebera-Vishkina
• Zapytanie o minimalny zakres i artykuł o najniższym wspólnym przodku w Topcoder
• Dokumentacja pakietu lca dla Haskella autorstwa Edwarda Kmetta, która zawiera algorytm losowej listy dostępu skośno-binarnego. Czysto funkcjonalne struktury danych dla slajdów LCA on-line dla tego samego pakietu.