Obliczenia rozproszone

Nie mylić ze zdecentralizowanym przetwarzaniem .

System rozproszony to system, którego komponenty znajdują się na różnych komputerach w sieci , które komunikują się i koordynują swoje działania poprzez przekazywanie sobie komunikatów. Obliczenia rozproszone to dziedzina informatyki zajmująca się badaniem systemów rozproszonych.

Komponenty systemu rozproszonego współdziałają ze sobą w celu osiągnięcia wspólnego celu. Trzy istotne wyzwania systemów rozproszonych to: utrzymanie współbieżności komponentów, przezwyciężenie braku globalnego zegara oraz zarządzanie niezależną awarią komponentów. Kiedy element jednego systemu ulegnie awarii, cały system nie ulegnie awarii. Przykłady systemów rozproszonych obejmują na architekturze SOA, gry online dla wielu graczy i aplikacje peer-to-peer .

Program komputerowy działający w systemie rozproszonym nazywany jest programem rozproszonym , a programowanie rozproszone to proces pisania takich programów. Istnieje wiele różnych typów implementacji mechanizmu przekazywania komunikatów, w tym czysty HTTP, łączniki podobne do RPC i kolejki komunikatów .

Przetwarzanie rozproszone odnosi się również do wykorzystania systemów rozproszonych do rozwiązywania problemów obliczeniowych. W przetwarzaniu rozproszonym problem jest podzielony na wiele zadań, z których każde jest rozwiązywane przez jeden lub więcej komputerów, które komunikują się ze sobą poprzez przekazywanie komunikatów.

Wstęp

Słowo dystrybuowane w terminach takich jak „system rozproszony”, „programowanie rozproszone” i „ algorytm rozproszony ” pierwotnie odnosiło się do sieci komputerowych, w których poszczególne komputery były fizycznie rozmieszczone na pewnym obszarze geograficznym. Terminy te są obecnie używane w znacznie szerszym znaczeniu, nawet w odniesieniu do autonomicznych procesów , które działają na tym samym fizycznym komputerze i wchodzą ze sobą w interakcje poprzez przekazywanie komunikatów.

Chociaż nie ma jednej definicji systemu rozproszonego, powszechnie używane są następujące właściwości definiujące:

System rozproszony może mieć wspólny cel, taki jak rozwiązanie dużego problemu obliczeniowego; użytkownik postrzega wówczas zbiór autonomicznych procesorów jako jednostkę. Alternatywnie każdy komputer może mieć własnego użytkownika o indywidualnych potrzebach, a celem systemu rozproszonego jest koordynacja wykorzystania współdzielonych zasobów lub świadczenie usług komunikacyjnych użytkownikom.

Inne typowe właściwości systemów rozproszonych to:

  • System musi tolerować awarie poszczególnych komputerów.
  • Struktura systemu (topologia sieci, opóźnienie sieci, liczba komputerów) nie jest z góry znana, system może składać się z różnego rodzaju komputerów i łączy sieciowych, a system może się zmieniać w trakcie wykonywania rozproszonego programu.
  • Każdy komputer ma tylko ograniczony, niepełny obraz systemu. Każdy komputer może znać tylko jedną część danych wejściowych.

Obliczenia równoległe i rozproszone


(a), (b): system rozproszony. (c): system równoległy.

Systemy rozproszone to grupy komputerów połączonych w sieć, które mają wspólny cel swojej pracy. Terminy „ przetwarzanie współbieżne ”, „ przetwarzanie równoległe ” i „przetwarzanie rozproszone” w dużym stopniu się pokrywają i nie ma między nimi wyraźnego rozróżnienia. Ten sam system można scharakteryzować zarówno jako „równoległy”, jak i „rozproszony”; procesory w typowym systemie rozproszonym działają równolegle. Obliczenia równoległe mogą być postrzegane jako szczególnie ściśle powiązana forma przetwarzania rozproszonego, a przetwarzanie rozproszone może być postrzegane jako luźno powiązana forma przetwarzania równoległego. Niemniej jednak możliwe jest z grubsza sklasyfikowanie systemów współbieżnych jako „równoległych” lub „rozproszonych” przy użyciu następujących kryteriów:

  • W obliczeniach równoległych wszystkie procesory mogą mieć dostęp do wspólnej pamięci w celu wymiany informacji między procesorami.
  • W obliczeniach rozproszonych każdy procesor ma swoją własną pamięć prywatną ( pamięć rozproszona ). Wymiana informacji odbywa się poprzez przekazywanie komunikatów między procesorami.

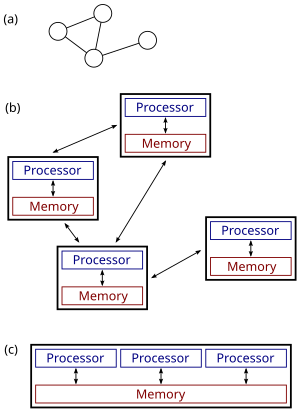
Rysunek po prawej ilustruje różnicę między systemami rozproszonymi i równoległymi. Rysunek (a) jest schematycznym widokiem typowego systemu rozproszonego; system jest reprezentowany jako topologia sieci, w której każdy węzeł jest komputerem, a każda linia łącząca węzły jest łączem komunikacyjnym. Rysunek (b) przedstawia bardziej szczegółowo ten sam system rozproszony: każdy komputer ma własną pamięć lokalną, a wymiana informacji może odbywać się tylko poprzez przekazywanie komunikatów z jednego węzła do drugiego za pomocą dostępnych łączy komunikacyjnych. Rysunek (c) przedstawia system równoległy, w którym każdy procesor ma bezpośredni dostęp do pamięci współdzielonej.

Sytuację dodatkowo komplikują tradycyjne zastosowania terminów algorytm równoległy i rozproszony , które nie do końca pasują do powyższych definicji systemów równoległych i rozproszonych ( bardziej szczegółowe omówienie poniżej ). Niemniej jednak, jako praktyczna zasada, wysokowydajne obliczenia równoległe w multiprocesorze z pamięcią współdzieloną wykorzystują algorytmy równoległe, podczas gdy koordynacja wielkoskalowego systemu rozproszonego wykorzystuje algorytmy rozproszone.

Historia

Wykorzystanie współbieżnych procesów, które komunikują się poprzez przekazywanie wiadomości, ma swoje korzenie w architekturach systemów operacyjnych badanych w latach 60. Pierwszymi szeroko rozpowszechnionymi systemami rozproszonymi były sieci lokalne, takie jak Ethernet , który został wynaleziony w latach 70.

ARPANET , jeden z poprzedników Internetu , został wprowadzony pod koniec lat 60., a poczta elektroniczna ARPANET została wynaleziona na początku lat 70. Poczta elektroniczna stała się najbardziej udaną aplikacją ARPANET i jest prawdopodobnie najwcześniejszym przykładem aplikacji rozproszonej na dużą skalę . Oprócz ARPANET (i jego następcy, globalnego Internetu), inne wczesne światowe sieci komputerowe obejmowały Usenet i FidoNet z lat 80., z których obie były używane do obsługi rozproszonych systemów dyskusyjnych.

Badanie przetwarzania rozproszonego stało się odrębną gałęzią informatyki pod koniec lat 70. i na początku lat 80. XX wieku. Pierwsza konferencja w tej dziedzinie, Symposium on Principles of Distributed Computing (PODC), sięga 1982 roku, a jej odpowiednik International Symposium on Distributed Computing (DISC) po raz pierwszy odbyło się w Ottawie w 1985 roku jako International Workshop on Distributed Algorithms on Graphs.

Architektury

Do przetwarzania rozproszonego wykorzystywane są różne architektury sprzętowe i programowe. Na niższym poziomie konieczne jest połączenie wielu procesorów z jakąś siecią, niezależnie od tego, czy ta sieć jest wydrukowana na płytce drukowanej, czy składa się z luźno połączonych urządzeń i kabli. Na wyższym poziomie konieczne jest połączenie procesów działających na tych procesorach z jakimś systemem komunikacyjnym .

Programowanie rozproszone zazwyczaj mieści się w jednej z kilku podstawowych architektur: klient-serwer , trójwarstwowa , n -warstwowa lub peer-to-peer ; lub kategorie: luźne sprzęgło lub ciasne sprzęgło .

  • Klient-serwer : architektury, w których inteligentni klienci kontaktują się z serwerem w celu uzyskania danych, a następnie formatują je i wyświetlają użytkownikom. Dane wejściowe po stronie klienta są przekazywane z powrotem do serwera, gdy reprezentują trwałą zmianę.
  • Trójwarstwowa : architektury, które przenoszą inteligencję klienta na warstwę środkową, aby można było używać klientów bezstanowych . Upraszcza to wdrażanie aplikacji. Większość aplikacji internetowych jest trójwarstwowa.
  • n -tier : architektury odnoszące się zazwyczaj do aplikacji internetowych, które dalej przekazują swoje żądania do innych usług korporacyjnych. Ten typ aplikacji jest najbardziej odpowiedzialny za sukces serwerów aplikacji .
  • Peer-to-peer : architektury, w których nie ma specjalnych maszyn świadczących usługi lub zarządzających zasobami sieciowymi. Zamiast tego wszystkie obowiązki są równomiernie podzielone między wszystkie maszyny, zwane równorzędnymi. Peers mogą służyć zarówno jako klienci, jak i jako serwery. Przykładami tej architektury są BitTorrent i sieć bitcoin .

Kolejnym podstawowym aspektem architektury przetwarzania rozproszonego jest sposób komunikowania się i koordynowania pracy między współbieżnymi procesami. Poprzez różne protokoły przekazywania komunikatów procesy mogą komunikować się bezpośrednio ze sobą, zwykle w nadrzędny/podrzędny . Alternatywnie, architektura „skoncentrowana na bazie danych” może umożliwić przetwarzanie rozproszone bez jakiejkolwiek formy bezpośredniej komunikacji między procesami , poprzez wykorzystanie współużytkowanej bazy danych . W szczególności architektura zorientowana na bazę danych zapewnia analizę przetwarzania relacyjnego w architekturze schematycznej, umożliwiającej przekazywanie środowiska na żywo. Umożliwia to funkcje obliczeń rozproszonych zarówno w ramach parametrów sieciowej bazy danych, jak i poza nimi.

Aplikacje

Powody korzystania z systemów rozproszonych i przetwarzania rozproszonego mogą obejmować:

  • Sam charakter aplikacji może wymagać użycia sieci komunikacyjnej, która łączy kilka komputerów: na przykład dane wytwarzane w jednej fizycznej lokalizacji i wymagane w innej lokalizacji.
  • Istnieje wiele przypadków, w których użycie pojedynczego komputera byłoby w zasadzie możliwe, jednak zastosowanie systemu rozproszonego jest korzystne ze względów praktycznych. Na przykład:
    • Może pozwolić na znacznie większą pamięć masową i pamięć, szybsze obliczenia i większą przepustowość niż pojedyncza maszyna.
    • Może zapewnić większą niezawodność niż system nierozproszony, ponieważ nie ma pojedynczego punktu awarii . Ponadto system rozproszony może być łatwiejszy w rozbudowie i zarządzaniu niż monolityczny system jednoprocesorowy.
    • klastra kilku komputerów klasy niższej może być bardziej opłacalne w porównaniu z pojedynczym komputerem klasy wyższej.

Przykłady

Przykłady systemów rozproszonych i aplikacji przetwarzania rozproszonego obejmują:

Podstawy teoretyczne

Główny artykuł: algorytm rozproszony

modele

Wiele zadań, które chcielibyśmy zautomatyzować za pomocą komputera, ma charakter pytanie-odpowiedź: chcielibyśmy zadać pytanie, a komputer powinien dać odpowiedź. W informatyce teoretycznej takie zadania nazywane są problemami obliczeniowymi . Formalnie problem obliczeniowy składa się z instancji wraz z rozwiązaniem dla każdej instancji. Instancje to pytania, które możemy zadać, a rozwiązania to pożądane odpowiedzi na te pytania.

Informatyka teoretyczna stara się zrozumieć, które problemy obliczeniowe można rozwiązać za pomocą komputera ( teoria obliczalności ) i jak wydajnie ( teoria złożoności obliczeniowej ). Tradycyjnie mówi się, że problem można rozwiązać za pomocą komputera, jeśli potrafimy zaprojektować algorytm, który daje poprawne rozwiązanie dla dowolnego przypadku. Taki algorytm można zaimplementować jako program komputerowy , który działa na komputerze ogólnego przeznaczenia: program odczytuje instancję problemu z input , wykonuje pewne obliczenia i generuje rozwiązanie jako wyjście . Formalizmy, takie jak maszyny o swobodnym dostępie lub uniwersalne maszyny Turinga, mogą być używane jako abstrakcyjne modele sekwencyjnego komputera ogólnego przeznaczenia wykonującego taki algorytm.

Dziedzina obliczeń współbieżnych i rozproszonych zajmuje się podobnymi pytaniami w przypadku wielu komputerów lub komputera wykonującego sieć oddziałujących na siebie procesów: jakie problemy obliczeniowe można rozwiązać w takiej sieci i jak wydajnie? Jednak wcale nie jest oczywiste, co należy rozumieć przez „rozwiązywanie problemu” w przypadku systemu współbieżnego lub rozproszonego: na przykład, jakie jest zadanie projektanta algorytmu i jaki jest współbieżny lub rozproszony odpowiednik komputer ogólnego przeznaczenia? [ potrzebne źródło ]

Poniższa dyskusja koncentruje się na przypadku wielu komputerów, chociaż wiele problemów jest takich samych w przypadku procesów współbieżnych działających na jednym komputerze.

Powszechnie stosowane są trzy punkty widzenia:

Algorytmy równoległe w modelu z pamięcią współdzieloną
  • Wszystkie procesory mają dostęp do wspólnej pamięci. Projektant algorytmu wybiera program wykonywany przez każdy procesor.
  • Jednym z modeli teoretycznych są używane równoległe maszyny o swobodnym dostępie (PRAM). Jednak klasyczny model PRAM zakłada synchroniczny dostęp do pamięci współdzielonej.
  • Programy z pamięcią współdzieloną można rozszerzyć na systemy rozproszone, jeśli podstawowy system operacyjny hermetyzuje komunikację między węzłami i wirtualnie ujednolica pamięć we wszystkich poszczególnych systemach.
  • Model, który jest bliższy zachowaniu rzeczywistych maszyn wieloprocesorowych i uwzględnia użycie instrukcji maszynowych, takich jak porównanie i zamiana (CAS), to asynchroniczna pamięć współdzielona . Istnieje wiele prac na temat tego modelu, których streszczenie można znaleźć w literaturze.
Algorytmy równoległe w modelu przekazywania komunikatów
  • Projektant algorytmu wybiera strukturę sieci, a także program wykonywany przez każdy komputer.
  • modele takie jak obwody boolowskie i sieci sortowania . Obwód logiczny można postrzegać jako sieć komputerową: każda bramka to komputer, na którym działa niezwykle prosty program komputerowy. Podobnie sieć sortującą można postrzegać jako sieć komputerową: każdy komparator to komputer.
Algorytmy rozproszone w modelu przekazywania komunikatów
  • Projektant algorytmu wybiera tylko program komputerowy. Na wszystkich komputerach działa ten sam program. System musi działać poprawnie niezależnie od struktury sieci.
  • Powszechnie stosowanym modelem jest graf z jedną maszyną skończoną na węzeł.

W przypadku algorytmów rozproszonych problemy obliczeniowe są zwykle związane z grafami. Często instancją problemu jest wykres opisujący strukturę sieci komputerowej . Ilustruje to poniższy przykład. [ potrzebne źródło ]

Przykład

Rozważ problem obliczeniowy znalezienia kolorowania danego grafu G . Różne dziedziny mogą przyjąć następujące podejścia:

Algorytmy scentralizowane [ potrzebne źródło ]
  • Graf G jest zakodowany jako ciąg znaków, który jest podawany jako dane wejściowe do komputera. Program komputerowy znajduje kolorowanie wykresu, koduje kolorowanie jako ciąg znaków i wyświetla wynik.
Algorytmy równoległe
  • Ponownie, wykres G jest zakodowany jako ciąg znaków. Jednak wiele komputerów może równolegle uzyskiwać dostęp do tego samego ciągu. Każdy komputer może skupić się na jednej części wykresu i stworzyć kolorowanie dla tej części.
  • Główny nacisk kładziony jest na obliczenia o wysokiej wydajności, które wykorzystują moc obliczeniową wielu komputerów równolegle.
Algorytmy rozproszone
  • Graf G to struktura sieci komputerowej. Jest jeden komputer dla każdego węzła G i jedno łącze komunikacyjne dla każdej krawędzi G. Początkowo każdy komputer wie tylko o swoich bezpośrednich sąsiadach z grafu G ; komputery muszą wymieniać między sobą wiadomości, aby dowiedzieć się więcej o strukturze G . Każdy komputer musi generować swój własny kolor jako wyjście.
  • Główny nacisk położony jest na koordynację działania dowolnego systemu rozproszonego. [ potrzebne źródło ]

Chociaż dziedzina algorytmów równoległych ma inny cel niż dziedzina algorytmów rozproszonych, istnieje wiele interakcji między tymi dwoma dziedzinami. Na przykład algorytm Cole'a-Vishkina do kolorowania grafów był pierwotnie przedstawiony jako algorytm równoległy, ale ta sama technika może być również użyta bezpośrednio jako algorytm rozproszony.

Co więcej, algorytm równoległy może być zaimplementowany albo w systemie równoległym (z wykorzystaniem pamięci współdzielonej), albo w systemie rozproszonym (z wykorzystaniem przekazywania komunikatów). Tradycyjna granica między algorytmami równoległymi i rozproszonymi (wybierz odpowiednią sieć vs. uruchom w dowolnej sieci) nie leży w tym samym miejscu, co granica między systemami równoległymi i rozproszonymi (pamięć współdzielona vs. przekazywanie komunikatów).

Miary złożoności

W algorytmach równoległych kolejnym zasobem oprócz czasu i przestrzeni jest liczba komputerów. Rzeczywiście, często istnieje kompromis między czasem działania a liczbą komputerów: problem można rozwiązać szybciej, jeśli jest więcej komputerów pracujących równolegle (patrz przyspieszenie ). Jeśli problem decyzyjny można rozwiązać w czasie polilogarytmicznym przy użyciu wielomianowej liczby procesorów, to mówi się, że problem należy do klasy NC . Klasę NC można równie dobrze zdefiniować za pomocą formalizmu PRAM lub obwodów boolowskich — maszyny PRAM mogą wydajnie symulować obwody boolowskie i odwrotnie.

W analizie algorytmów rozproszonych zwykle więcej uwagi poświęca się operacjom komunikacyjnym niż krokom obliczeniowym. Być może najprostszym modelem przetwarzania rozproszonego jest system synchroniczny, w którym wszystkie węzły działają w sposób blokujący. Model ten jest powszechnie znany jako model LOKALNY. Podczas każdej rundy komunikacji wszystkie węzły równolegle (1) odbierają najnowsze komunikaty od swoich sąsiadów, (2) wykonują dowolne lokalne obliczenia i (3) wysyłają nowe komunikaty do swoich sąsiadów. W takich systemach główną miarą złożoności jest liczba synchronicznych rund komunikacyjnych wymaganych do wykonania zadania.

Ta miara złożoności jest ściśle związana ze średnicą sieci. Niech D będzie średnicą sieci. Z jednej strony każdy problem obliczeniowy można rozwiązać trywialnie w synchronicznym systemie rozproszonym w około 2-wymiarowych rundach komunikacyjnych: wystarczy zebrać wszystkie informacje w jednym miejscu ( D rund), rozwiązać problem i poinformować każdy węzeł o rozwiązaniu ( D rund ).

Z drugiej strony, jeśli czas działania algorytmu jest znacznie mniejszy niż D rund komunikacyjnych, to węzły w sieci muszą generować swoje dane wyjściowe bez możliwości uzyskania informacji o odległych częściach sieci. Innymi słowy, węzły muszą podejmować globalnie spójne decyzje w oparciu o informacje dostępne w ich lokalnym D-sąsiedztwie . Znanych jest wiele rozproszonych algorytmów, których czas działania jest znacznie krótszy niż D , a zrozumienie, które problemy można rozwiązać za pomocą takich algorytmów, jest jednym z głównych pytań badawczych w tej dziedzinie. Zazwyczaj algorytm, który rozwiązuje problem w czasie polilogarytmicznym w rozmiarze sieci, jest uważany za efektywny w tym modelu.

Inną często stosowaną miarą jest całkowita liczba bitów przesyłanych w sieci (por. złożoność komunikacji ). Cechy tej koncepcji są zazwyczaj uchwycone za pomocą modelu CONGEST(B), który jest podobnie zdefiniowany jak model LOKALNY, ale w którym pojedyncze komunikaty mogą zawierać tylko B bitów.

Inne problemy

Tradycyjne problemy obliczeniowe przyjmują perspektywę, w której użytkownik zadaje pytanie, komputer (lub system rozproszony) przetwarza pytanie, a następnie generuje odpowiedź i zatrzymuje się. Istnieją jednak również problemy, w przypadku których system musi się nie zatrzymywać, w tym problem filozofów jedzących i inne podobne problemy wzajemnego wykluczania się . W tych problemach system rozproszony ma stale koordynować wykorzystanie współdzielonych zasobów, tak aby nie dochodziło do konfliktów lub zakleszczeń .

Istnieją również fundamentalne wyzwania, które są unikalne dla przetwarzania rozproszonego, na przykład związane z odpornością na błędy . Przykłady powiązanych problemów obejmują problemy konsensusu , bizantyjską tolerancję błędów i samostabilizację .

Wiele badań koncentruje się również na zrozumieniu asynchronicznej natury systemów rozproszonych:

Wybór

Wybór koordynatora (lub wybór lidera ) to proces wyznaczania pojedynczego procesu jako organizatora jakiegoś zadania rozdzielonego na kilka komputerów (węzłów). Przed rozpoczęciem zadania wszystkie węzły sieci albo nie wiedzą, który węzeł będzie pełnił funkcję „koordynatora” (lub lidera) zadania, albo nie będą mogły komunikować się z bieżącym koordynatorem. Jednak po uruchomieniu algorytmu wyboru koordynatora każdy węzeł w sieci rozpoznaje konkretny, unikalny węzeł jako koordynatora zadania.

Węzły sieci komunikują się między sobą, aby zdecydować, który z nich przejdzie w stan „koordynatora”. W tym celu potrzebują jakiejś metody, aby przełamać symetrię między nimi. Na przykład, jeśli każdy węzeł ma unikalne i porównywalne tożsamości, wtedy węzły mogą porównać swoje tożsamości i zdecydować, że węzeł o najwyższej tożsamości jest koordynatorem.

Definicja tego problemu jest często przypisywana LeLannowi, który sformalizował go jako metodę tworzenia nowego tokena w sieci Token Ring , w której token został utracony.

Algorytmy wyboru koordynatora są zaprojektowane tak, aby były ekonomiczne pod względem całkowitej liczby przesłanych bajtów i czasu. Algorytm zaproponowany przez Gallagera, Humbleta i Spirę dla ogólnych grafów nieskierowanych wywarł duży wpływ na ogólne projektowanie algorytmów rozproszonych i zdobył nagrodę Dijkstry za wpływową pracę dotyczącą przetwarzania rozproszonego.

Zaproponowano wiele innych algorytmów dla różnych rodzajów grafów sieciowych , takich jak pierścienie niekierowane, pierścienie jednokierunkowe, pełne grafy, siatki, skierowane grafy Eulera i inne. Ogólną metodę, która oddziela kwestię rodziny grafów od projektu algorytmu wyboru koordynatora, zaproponowali Korach, Kutten i Moran.

W celu przeprowadzenia koordynacji systemy rozproszone wykorzystują koncepcję koordynatorów. Problem wyboru koordynatora polega na wybraniu procesu spośród grupy procesów na różnych procesorach w systemie rozproszonym, który będzie pełnił rolę centralnego koordynatora. Istnieje kilka algorytmów wyboru centralnego koordynatora.

Właściwości systemów rozproszonych

Dotychczas koncentrowano się na zaprojektowaniu systemu rozproszonego, który rozwiązuje zadany problem. Uzupełniającym problemem badawczym jest badanie właściwości danego systemu rozproszonego.

Problem zatrzymania jest analogicznym przykładem z dziedziny obliczeń scentralizowanych: otrzymujemy program komputerowy, a zadaniem jest zdecydować, czy się zatrzyma, czy będzie działał w nieskończoność. Problem zatrzymania jest nierozstrzygalny i oczywiście zrozumienie zachowania sieci komputerowej jest co najmniej tak trudne, jak zrozumienie zachowania jednego komputera.

Istnieje jednak wiele interesujących przypadków specjalnych, które można rozstrzygnąć. W szczególności możliwe jest wnioskowanie o zachowaniu sieci maszyn skończonych. Jednym z przykładów jest stwierdzenie, czy dana sieć oddziałujących na siebie (asynchronicznych i niedeterministycznych) maszyn skończonych może znaleźć się w impasie. Ten problem jest PSPACE-zupełny , tj. jest rozstrzygalny, ale jest mało prawdopodobne, że istnieje wydajny (scentralizowany, równoległy lub rozproszony) algorytm, który rozwiązuje problem w przypadku dużych sieci.

Zobacz też

Notatki

Książki
Artykuły
Witryny internetowe

Dalsza lektura

Książki
Artykuły
Materiały konferencyjne
  •   Rodriguez, Carlos; Villagra, Marcos; Baran, Benjamin (2007). „Algorytmy zespołu asynchronicznego dla spełnialności logicznej”. 2007 2. inspirowane biologią modele sieci, systemów informacyjnych i komputerowych . s. 66–69. doi : 10.1109/BIMNICS.2007.4610083 . S2CID 15185219 .

Linki zewnętrzne

Pobrano z „ https://en.wikipedia.org/w/index.php?title=Distributed_computing&oldid=1139728172 ”