Nieobojętne plazmy
Plazma nieobojętna to plazma , której ładunek wypadkowy tworzy pole elektryczne wystarczająco duże, aby odgrywać ważną lub nawet dominującą rolę w dynamice plazmy. Najprostsze plazmy nieobojętne to plazmy składające się z pojedynczego rodzaju ładunku. Przykładami nieobojętnych plazm pojedynczych gatunków, które zostały utworzone w eksperymentach laboratoryjnych, są plazmy składające się wyłącznie z elektronów , plazmy czystych jonów , plazmy pozytonowe i plazmy antyprotonowe.
Plazmy nieneutralne są wykorzystywane do badań podstawowych zjawisk plazmy, takich jak transport pola magnetycznego, nieliniowe oddziaływania wirowe oraz fale i niestabilności plazmy . Zostały również wykorzystane do stworzenia zimnej, neutralnej antymaterii poprzez staranne mieszanie i rekombinację kriogenicznej plazmy czystego pozytonu i czystego antyprotonu. Plazmy pozytonowe są również wykorzystywane w eksperymentach fizyki atomowej , które badają oddziaływanie antymaterii z neutralnymi atomami i cząsteczkami. Kriogeniczne plazmy czystych jonów zostały wykorzystane w badaniach silnie sprzężonych plazm i splątanie kwantowe . Bardziej prozaicznie, czysta plazma elektronowa jest używana do wytwarzania mikrofal w kuchenkach mikrofalowych, poprzez niestabilność magnetronu .
Plazmy neutralne w kontakcie z powierzchnią stałą (czyli większość plazm laboratoryjnych) są zazwyczaj nieobojętne w obszarach brzegowych. Ze względu na nierówne tempo utraty elektronów i jonów na powierzchnię, tworzy się pole elektryczne ( „pole ambipolarne” ), które powstrzymuje bardziej ruchliwe gatunki, dopóki współczynniki utraty nie będą takie same. Potencjał elektrostatyczny (mierzony w elektronowoltach) wymagany do wytworzenia tego pola elektrycznego zależy od wielu zmiennych, ale często jest rzędu temperatury elektronów.
Nieobojętne plazmy, dla których wszystkie gatunki mają ten sam znak ładunku, mają wyjątkowe właściwości ograniczające w porównaniu z plazmami obojętnymi. Można je zamknąć w równowagi termicznej , używając tylko statycznych pól elektrycznych i magnetycznych, w konfiguracji pułapki Penninga (patrz ryc. 1). Osiągnięto czasy zamknięcia do kilku godzin. Stosując metodę „obrotowej ściany” , czas utrzymywania plazmy można dowolnie zwiększać.
Takie nieobojętne plazmy mogą również uzyskać dostęp do nowych stanów materii. Na przykład można je schłodzić do temperatur kriogenicznych bez rekombinacji (ponieważ nie ma gatunków o przeciwnym ładunku, z którymi można by rekombinować). Jeśli temperatura jest wystarczająco niska (zwykle rzędu 10 mK), plazma może stać się nieobojętną cieczą lub kryształem . Sześcienna skupiona na ciele tych kryształów plazmy została zaobserwowana przez rozpraszanie Bragga w eksperymentach na chłodzonej laserowo plazmie czystego berylu.
Równowaga pojedynczego gatunku nieobojętnej plazmy

Nieobojętne plazmy z pojedynczym znakiem ładunku mogą być utrzymywane przez długi czas przy użyciu wyłącznie statycznych pól elektrycznych i magnetycznych. Jedna taka konfiguracja nazywana jest pułapką Penninga , na cześć wynalazcy FM Penninga . Cylindryczna wersja pułapki jest czasami nazywana pułapką Penninga-Malmberga, od nazwiska prof. Johna Malmberga. Pułapka składa się z kilku cylindrycznie symetrycznych elektrod i jednorodnego pola magnetycznego przyłożonego wzdłuż osi pułapki (ryc. 1). Plazma jest ograniczana w kierunku osiowym przez polaryzację elektrod końcowych w taki sposób, aby utworzyć osiową studnię potencjału, która zatrzyma ładunki o danym znaku (na rysunku zakłada się, że znak jest dodatni). W kierunku promieniowym ograniczenie zapewnia tzw v × B Siła Lorentza spowodowana obrotem plazmy wokół osi pułapki. Rotacja plazmy powoduje skierowaną do wewnątrz siłę Lorentza, która po prostu równoważy siły skierowane na zewnątrz spowodowane przez niezobojętnioną plazmę, jak również siłę odśrodkową. Matematycznie równowaga sił promieniowych implikuje równowagę między siłami elektrycznymi, magnetycznymi i odśrodkowymi:
-
()
gdzie zakłada się, że cząstki mają masę Er m i ładunek q , r to promieniowa odległość od osi pułapki, a to promieniowa składowa pola elektrycznego. To równanie kwadratowe można rozwiązać dla prędkości obrotowej rozwiązania z wolnymi obrotami i szybkoobrotowymi Szybkość obrotu dla tych dwóch rozwiązań można zapisać jako
- ,
gdzie jest częstotliwością cyklotronu . W zależności od promieniowego pola elektrycznego, rozwiązania dla prędkości obrotowej mieszczą się w zakresie . Wolny i szybki tryb rotacji spotykają się, gdy pole elektryczne jest takie, że . Nazywa się to granicą Brillouina; jest to równanie maksymalnego możliwego promieniowego pola elektrycznego, które umożliwia uwięzienie plazmy.
To promieniowe pole elektryczne można powiązać z gęstością plazmy n za pomocą równania Poissona ,
i to równanie można wykorzystać do uzyskania związku między gęstością a szybkością rotacji plazmy. Jeśli założymy, że prędkość rotacji jest jednostajna w promieniu (tj. plazma obraca się jako ciało sztywne), to Równanie. (1) implikuje, że promieniowe pole elektryczne jest proporcjonalne do promienia r . Rozwiązanie dla E r z tego równania w kategoriach i podstawienie wyniku do równania Poissona daje
-
()
To równanie implikuje, że maksymalna możliwa gęstość występuje na granicy Brillouina i ma wartość
gdzie _ Zatem gęstość energii spoczynkowej plazmy, n·m·c 2 , jest mniejsza lub równa gęstości energii magnetycznej pola magnetycznego. Jest to dość surowe wymaganie dotyczące gęstości. Dla pola magnetycznego o natężeniu 10 tesli gęstość Brillouina dla elektronów wynosi tylko n B = 4,8 × 10 14 cm -3 .
Gęstość przewidziana przez równanie (2), przeskalowana przez gęstość Brillouina, jest pokazana jako funkcja prędkości obrotowej na ryc. (2). Dwie prędkości obrotowe dają tę samą gęstość, odpowiadającą rozwiązaniom z wolnymi i szybkimi obrotami.
Procesy utraty plazmy; metoda obracającej się ściany
W eksperymentach na plazmach pojedynczych gatunków częstość rotacji plazmy w zakresie dziesiątek kHz nie jest rzadkością, nawet w trybie wolnej rotacji. Ta szybka rotacja jest konieczna, aby zapewnić ograniczającą promieniową siłę Lorentza dla plazmy. Jeśli jednak w pułapce znajduje się gaz obojętny, zderzenia między plazmą a gazem powodują spowolnienie rotacji plazmy, co prowadzi do promieniowego rozszerzania się plazmy, aż zetknie się ona z otaczającymi elektrodami i zostanie utracona. Ten proces utraty można złagodzić, operując pułapką w bardzo wysokiej próżni. Jednak nawet w takich warunkach rotacja plazmy może nadal zostać spowolniona poprzez interakcję plazmy z „błędami” w zewnętrznych polach ograniczających. Jeśli te pola nie są idealnie cylindrycznie symetryczne, asymetrie mogą oddziaływać na plazmę, zmniejszając prędkość obrotową. Takie błędy w terenie są nieuniknione w każdym rzeczywistym eksperymencie i ograniczają czas utrzymywania plazmy.
Możliwe jest przezwyciężenie tego mechanizmu utraty plazmy poprzez zastosowanie błędu pola wirującego do plazmy. Jeśli błąd obraca się szybciej niż plazma, działa w celu rozkręcenia plazmy (podobnie jak wirujące ostrze blendera powoduje wirowanie żywności), przeciwdziałając efektowi błędów pola, które są nieruchome w ramie laboratorium. Ten błąd pola wirującego jest określany jako „obrotowa ściana”, zgodnie z teorią, że można odwrócić efekt asymetrii pułapki, po prostu obracając całą pułapkę z częstotliwością rotacji plazmy. Ponieważ jest to niepraktyczne, zamiast tego obraca się pole elektryczne pułapki, a nie całą pułapkę, przykładając odpowiednio fazowane napięcia do zestawu elektrod otaczających plazmę.
Gdy nieobojętna plazma jest schładzana do temperatur kriogenicznych, nie ulega rekombinacji w gaz obojętny, tak jak plazma obojętna, ponieważ nie ma cząstek o ładunku przeciwnym, z którymi mogłaby się rekombinować. W rezultacie system może uzyskać dostęp do nowych, silnie sprzężonych, nieobojętnych stanów materii, w tym kryształów plazmy składających się wyłącznie z pojedynczych rodzajów ładunków. Te silnie sprzężone nieobojętne plazmy są parametryzowane przez parametr sprzężenia Γ, zdefiniowany jako
gdzie to temperatura, a – Seitza lub średni odstęp międzycząsteczkowy), określony jako gęstość wyrażeniem π T . Parametr sprzężenia można traktować jako stosunek średniej energii interakcji między parami najbliższych sąsiadów, i średnia energia kinetyczna rzędu . Kiedy ten stosunek jest mały, oddziaływania są słabe, a plazma jest prawie idealnym gazem ładunków poruszających się w średnim polu wytwarzanym przez inne ładunki. Jednakże, gdy są ważne, a plazma zachowuje się bardziej jak ciecz, a nawet kryształ, jeśli jest wystarczająco duży. W rzeczywistości symulacje komputerowe i teoria przewidywały, że dla nieskończonej jednorodnej plazmy system wykazuje stopniowy początek uporządkowania bliskiego zasięgu, zgodny ze stanem podobnym do cieczy dla i jest Γ przewiduje się, że będzie to przejście fazowe pierwszego rzędu do sześciennego kryształu skupionego na ciele dla .
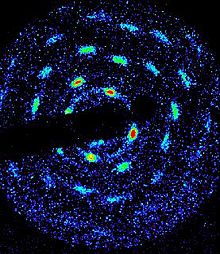
Eksperymenty zaobserwowały ten stan krystaliczny w czystej plazmie jonów berylu, która została schłodzona laserem do zakresu temperatur milikelwinów. Średnie odstępy międzycząsteczkowe w tym czystym krysztale jonowym były rzędu 10-20 µm , znacznie większe niż w obojętnej materii krystalicznej. Odstęp ten odpowiada gęstości rzędu 10 8-10 9 cm -3 , nieco mniejszej niż granica Brillouina dla berylu w polu magnetycznym 4,5 tesli w eksperymencie. Następnie wymagane były temperatury kriogeniczne, aby uzyskać wartość w systemie silnie sprzężonym. Eksperymenty zmierzyły strukturę kryształu za pomocą rozpraszania Bragga , w której skolimowana wiązka laserowa była rozpraszana od kryształu, wyświetlając piki Bragga pod oczekiwanymi kątami rozpraszania dla sieci bcc (patrz ryc. 3).
Gdy niewielka liczba jonów jest chłodzona laserem, tworzą one krystaliczne „skupiska kulombowskie”. Symetria klastra zależy od postaci zewnętrznych pól ograniczających. Interaktywny widok 3D niektórych gromad można znaleźć tutaj .
























