Odrodzenie kwantowe

Pełne i dokładne odrodzenie półgaussowskiej funkcji falowej w nieskończonej dwuwymiarowej studni potencjału podczas jej ewolucji w czasie. Pomiędzy ułamkowymi ożywieniami występują, gdy przeskalowany kształt funkcji falowej powiela się całkowitą liczbę razy w obszarze odwiertu.

W mechanice kwantowej odrodzenie kwantowe jest okresowym powrotem kwantowej funkcji falowej z jej pierwotnej postaci podczas ewolucji czasowej albo wielokrotnie w przestrzeni jako wielokrotne ułamki skalowane w postaci początkowej funkcji falowej (odrodzenie ułamkowe), albo w przybliżeniu lub dokładnie do swojej pierwotnej postaci od początku (pełne odrodzenie). Okresowa funkcja fali kwantowej w czasie wykazuje zatem pełne odrodzenie w każdym okresie . Zjawisko ożywień najłatwiej zaobserwować dla funkcji falowych, które są dobrze zlokalizowanymi pakietami falowymi na początku ewolucji czasu, na przykład w atomie wodoru. W przypadku wodoru ułamkowe przebudzenia pojawiają się jako wielokrotne kątowe wypukłości Gaussa wokół okręgu narysowanego przez promieniowe maksimum wiodącej kołowej składowej stanu (tej o najwyższej amplitudzie w rozwinięciu stanu własnego) pierwotnego zlokalizowanego stanu i pełnego odrodzenia jako oryginalnego Gaussa . Pełne przebudzenia są dokładne dla nieskończonej studni kwantowej , oscylatora harmonicznego lub atomu wodoru , podczas gdy dla krótszych czasów są przybliżone dla atomu wodoru i wielu układów kwantowych.

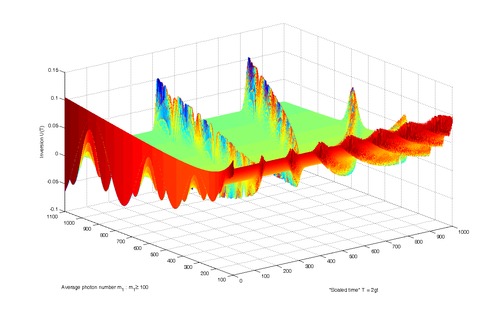
Wykres załamań i ożywień oscylacji kwantowych inwersji atomowej JCM.

Przykład - dowolna obcięta funkcja falowa układu kwantowego o energiach wymiernych

Rozważmy system kwantowy z energiami $displaystyle E_ {i$ stanami własnymi mi $}}$

${\ Displaystyle H \ psi _ {i} = E_ {i} \ psi _ {i}}$

i niech energie będą wymiernymi ułamkami jakiejś stałej do {\ displaystyle $}$

${\ Displaystyle E_ {i} = C {M_ {i} \ ponad N_ {i}}}$

(na przykład dla atomu wodoru ${\ Displaystyle M_ {i} = 1}$ , ${\ Displaystyle N_ {i} = i ^ {2}}$ , ${\ Displaystyle C=-13,6eV}$ .

Wtedy okrojone (do stanów) rozwiązanie zależnego od czasu równania Schrödingera to ${\ Displaystyle \ mathbb {N} _ {max}}}$

${\ Displaystyle \ Psi (t) = \ suma _ {i = 0} ^ {\ mathbb {N} _ {max }}a_{i}e^{-i{{E_{i}} \over \hbar }t}\psi _{i}}$

Superodrodzenie inwersji (powrót pełnych przybliżonych przebudzeń do pierwotnego kształtu) w modelu Jaynesa-Cummingsa, gdy dokładne widmo w rezonansie wokół średniej liczby fotonów jest przybliżone przez ${\ displaystyle n_ {0} = 100}$ wielomian w fotonie liczba kwantowa ${\ Displaystyle n}$${\ Displaystyle E (n) = a \ delta n ^ {2} + b \ delta n + c }$ , ${\ Displaystyle \ delta n = nn_ {0}}$

.

Niech $}}$$\ Displaystyle L_ {cd}}$ będzie najmniejszą wspólną wielokrotnością wszystkich ${$ L wspólnym dzielnikiem wszystkich $i}}$${\ displaystyle M_$${L_ {cm}}/N_ {i}}$ to dla każdego $ja {\$ Displaystyle liczbą całkowitą dla ${i}}$${\ Displaystyle {M_ {i}} / L_ {cd}}$ M jest liczbą całkowitą, ${\ Displaystyle 2 \ pi M_ {i} {L_ {cm}}/(N_ {i} L_ {cd})} jest$ pełną wielokrotnością kąta i ${\ Displaystyle 2 \ pi}$

${\ Displaystyle \ psi (t) = \ psi (t + T)}$

po pełnym czasie odrodzenia

${\ Displaystyle T = {2 \ pi \ hbar \ ponad {L_ {cd} C}} L_ {cm}$ .

W przypadku układu kwantowego tak małego jak wodór i $100$ może minąć kwadrylion lat, zanim w pełni odżyje Zwłaszcza raz utworzony przez pola pakiet fal trojańskich w atomie wodoru istnieje bez żadnych zewnętrznych pól stroboskopowo i wiecznie powtarzając się po przemiataniu prawie całego hipersześcianu faz kwantowych dokładnie w każdym pełnym czasie odrodzenia.

Uderzającą konsekwencją jest to, że żaden komputer skończony-bitowy nie może dokładnie propagować numerycznej funkcji falowej przez dowolnie długi czas. Jeżeli numer procesora jest n- bitową liczbą zmiennoprzecinkową to liczba może być zapamiętana przez komputer tylko ze skończoną dokładnością po przecinku a energia wynosi (do 8 cyfr po przecinku) np. 2,34576893 = 234576893/100000000 i jako ułamek skończony jest dokładnie wymierny i pełne odrodzenie następuje dla dowolnej funkcji falowej dowolnego układu kwantowego po czasie ${\ displaystyle t/2 \ pi = 100000000}$ , co jest jego maksymalnym wykładnikiem i tak dalej, co może nie być prawdą dla wszystkich systemów kwantowych lub wszystkich stacjonarnych systemów kwantowych, które przechodzą pełne i dokładne odrodzenie liczbowe.

W układzie z energiami wymiernymi, czyli tam, gdzie istnieje dokładnie kwantowe pełne odrodzenie, jego istnienie natychmiast dowodzi kwantowego twierdzenia Poincarégo o rekurencji , a czas pełnego ożywienia kwantowego jest równy czasowi rekurencji Poincarégo. Podczas gdy liczby wymierne są gęste w liczbach rzeczywistych, a dowolną funkcję liczby kwantowej można przybliżyć dowolnie dokładnie przybliżeniami Padé ze współczynnikami o dowolnej precyzji dziesiętnej przez dowolnie długi czas, każdy system kwantowy odradza się zatem prawie dokładnie. Oznacza to również, że rekurencja Poincarégo i pełne odrodzenie są matematycznie tym samym i powszechnie przyjmuje się, że rekurencja nazywana jest pełnym odrodzeniem, jeśli następuje po rozsądnym i fizycznie mierzalnym czasie, który jest możliwy do wykrycia przez realistyczną aparaturę i dzieje się tak z powodu bardzo specjalnego widma energii, które ma dużą lukę w odstępach energii podstawowej, której energie są arbitralnymi (niekoniecznie harmonicznymi) wielokrotnościami.