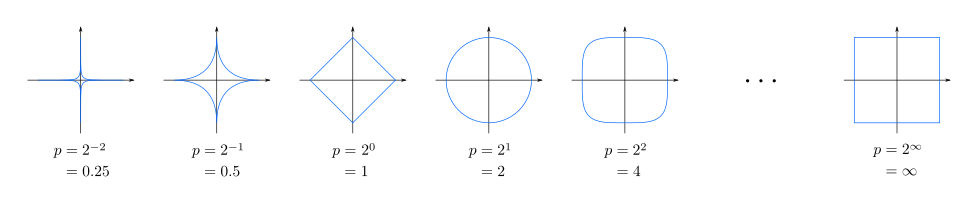Odległość Minkowskiego

Odległość Minkowskiego lub metryka Minkowskiego to metryka w znormalizowanej przestrzeni wektorowej , którą można uznać za uogólnienie zarówno odległości euklidesowej , jak i odległości Manhattanu . Jej nazwa pochodzi od niemieckiego matematyka Hermanna Minkowskiego .

Definicja

Odległość rzędu Minkowskiego (gdzie jest liczbą całkowitą) między dwoma punktami $}$ $displaystyle p$

{\ Displaystyle X = (x_ {1}, x_ {2}, \

jest zdefiniowany jako:

{\ Displaystyle D \ lewo (X, Y \ prawo) = \ lewo (\ suma _ {i = 1} ^ {n} | x_ {i} -y_ {i} | ^ {p} \ prawo) ^ {\ ułamek {1}{p}}.}

Dla ${\ Displaystyle p \ geq 1,}$ odległość Minkowskiego jest metryką wynikającą z nierówności Minkowskiego . p ${\ Displaystyle p <1,}$ odległość między $\ Displaystyle (0,0)}$ i ${\ Displaystyle (1,1)}$ wynosi $ale$ $2,}$ punkt znajduje się w pewnej odległości $.$ obu tych $Ponieważ$ narusza to nierówność trójkąta dla jest to metryka Jednak dla tych wartości można uzyskać metrykę, po prostu usuwając wykładnik ${\ Displaystyle 1/p.}$ Wynikowa metryka jest również normą F.

Zwykle używa się odległości Minkowskiego, gdzie $ona$ 1 lub 2, co odpowiada odpowiednio odległości Manhattanu i odległości euklidesowej . W granicznym przypadku osiągnięcia nieskończoności otrzymujemy odległość Czebyszewa : ${\ displaystyle p}$

{\ Displaystyle \ lim _ {p \ do \ infty}} {\ lewo (\ suma _ {i = 1} ^ {n} | x_ {i} -y_ {i} | ^ {p} \ prawej) ^ {\ ułamek {1}{p}}}=\max _{i=1}^{n}|x_{i}-y_{i}|.}

Podobnie, dla osiągnięcia ujemnej nieskończoności mamy: ${\ displaystyle p}$

{\ Displaystyle \ lim _ {p \ do - \ infty}} {\ lewo (\ suma _ {i = 1} ^ {n} | x_ {i} -y_ {i} | ^ {p} \ prawo) ^ { \frac {1}{p}}}=\min _{i=1}^{n}|x_{i}-y_{i}|.}

$Q$ Minkowskiego można również postrzegać jako wielokrotność średniej potęgi ${\ Displaystyle P.}$ różnic między i

Poniższy rysunek przedstawia okręgi jednostkowe ( zestaw poziomów funkcji odległości, w którym wszystkie punkty znajdują się w odległości jednostkowej od środka) z różnymi wartościami: ${\ displaystyle p}$ :

Zobacz też

Średnia uogólniona – N-ty pierwiastek ze średniej arytmetycznej danych liczb podniesiony do potęgi n
${\ displaystyle L ^ {p}}$ przestrzeń - Przestrzenie funkcyjne uogólniające skończenie wymiarowe p przestrzenie normowe
Norma (matematyka) – Długość w przestrzeni wektorowej
${\ displaystyle p}$ -norm - Przestrzenie funkcyjne uogólniające skończenie wymiarowe przestrzenie normowe p

Linki zewnętrzne