Odpływ Ellisa

Odpływ Ellisa jest najwcześniejszym znanym kompletnym modelem matematycznym tunelu czasoprzestrzennego, który można przebyć . Jest to statyczne, sferycznie symetryczne rozwiązanie równań pola próżni Einsteina wzmocnione przez włączenie pola skalarnego $minimalnie$ z geometrią czasoprzestrzeni z polaryzacją sprzężenia przeciwną do polaryzacji ortodoksyjnej (ujemna zamiast dodatniej ):

${\ Displaystyle {\ mathbf {R}} _ {\ mu \ nu} - \ textstyle {\ Frac {1} {2}} {\ mathbf {R}} \ g_ {\ mu \ nu} = - 2 \ ,\left(\phi _{,\mu }\phi _{,\nu }-\textstyle {\frac {1}{2}}\phi ^{,\kappa }\phi _{,\kappa }\ ,g_{\mu \nu }\right)\,.}$

Przegląd

Rozwiązanie zostało znalezione w 1969 roku (data pierwszego zgłoszenia) przez Homera G. Ellisa i niezależnie, mniej więcej w tym samym czasie, przez Kirill A. Bronnikova. Bronnikow zwrócił uwagę, że dwuwymiarowym odpowiednikiem topologii rozwiązania jest hiperboloida jednego arkusza, a jedynie zastosowanie antyortodoksyjnej polaryzacji sprzężenia pozwoliłoby na rozwiązanie o takiej topologii. Ellis, którego motywacją było znalezienie nieosobliwego zamiennika dla modelu Schwarzschilda elementarnej cząstki grawitacyjnej, wykazał, że wystarczyłaby tylko antyortodoksyjna biegunowość, ale znalazł wszystkie rozwiązania dla obu biegunowości, podobnie jak Bronnikow. Zbadał geometrię rozmaitości rozwiązań dla polaryzacji antyortodoksyjnej ze znaczną głębokością i stwierdził, że tak jest

• złożony z dwóch asymptotycznie płaskich trójwymiarowych obszarów połączonych w dwusferę („odpływ”),
• osobliwości ,
• pozbawione jednokierunkowych horyzontów zdarzeń ,
• geodezyjnie kompletne
• przyciągający grawitacyjnie po jednej stronie studzienki i silniej odpychający po drugiej,
• 
  
  wyposażony w podobne do czasu pole wektorowe, które zinterpretował jako pole prędkości „eteru” płynącego ze spoczynku w nieskończoności po stronie przyciągającej, w dół do otworu ściekowego i na zewnątrz do nieskończoności po stronie odpychającej , „tworząc” (lub reagując na) grawitację przez przyspieszenie do końca i
• przejezdne przez otwór spustowy w dowolnym kierunku dla fotonów i cząstek testowych .

Artykuł Chetouaniego i Clémenta nadał nazwę „geometria Ellisa” szczególnemu przypadkowi odpływu, w którym eter nie płynie i nie ma grawitacji, podobnie jak list do redaktora napisany przez Clémenta. Ten szczególny przypadek jest często określany jako „ tunel czasoprzestrzenny Ellisa ”. Kiedy pełnowymiarowy odpływ jest uważany za prototypowy tunel czasoprzestrzenny, po którym można przejść, obok nazwiska Ellisa dołącza się do niego imię Bronnikowa.

Rozwiązanie drenażu

Przekrój równikowy tunelu czasoprzestrzennego Ellisa ( nie odpływu), katenoidu do $\ displaystyle {\ mathcal {C}}}$

Wyobraź sobie dwie płaszczyzny euklidesowe, jedną nad drugą. Wybierz dwa okręgi o tym samym promieniu, jeden nad drugim, i usuń ich wnętrza. Teraz sklej elementy zewnętrzne razem w okręgach, zginając je płynnie, aby nie było ostrych krawędzi podczas klejenia. $przedstawiony$ ostrożnie, wynikiem będzie katenoid po prawej stronie lub coś podobnego. Następnie wyobraź sobie całą połączoną górną i dolną przestrzeń wypełnioną płynem wpływającym bez wirowania do otworu z góry i z dolnej strony, nabierając prędkości do końca i wyginając dolny obszar w bardziej stożkowy kształt niż widać na ${\ displaystyle {\ mathcal {C}}.}$ Jeśli wyobrazisz sobie przejście tego filmu z płaskiego ekranu do 3D, zastąpienie płaszczyzn euklidesowymi trzema przestrzeniami i okręgów sferami, i pomyśl o płynie płynącym ze wszystkich kierunków do otwór od góry i od dołu z niezmienionymi kierunkami, będziesz miał całkiem dobre pojęcie o tym, czym jest „odpływ”. Techniczny opis odpływu jako rozmaitości czasoprzestrzennej zawiera metryka czasoprzestrzenna opublikowana w 1973 roku.

${\ displaystyle c}$ wyraźną obecnością) do

${\ Displaystyle {\ rozpocząć {wyrównane} c ^ {2} d \ tau ^ {2} i = c ^ {2} dt ^{2}-[d\rho -f(\rho )\,c\,dt]^{2}-r^{2}(\rho )\,d\Omega ^{2}\\&=\ left[1-f^{2}(\rho )\right]\,c^{2}dT^{2}-{\frac {1}{1-f^{2}(\rho )}}\ ,d\rho ^{2}-r^{2}(\rho )\,d\Omega ^{2}\end{wyrównane}}\,,}$

gdzie ${\ Displaystyle \; \; d \ Omega ^ {2} = d \ vartheta ^ {2} + (\ sin \ vartheta) ^ {2 }d\varphi ^{2}\;\;}$ i ${\ Displaystyle \; \; T = t + {\ Displaystyle {\ Frac {1} {c}} \! \ int \! \! \! {\ Frac {f (\ rho)} {1-f ^ {2 }(\rho )}}\,d\rho \,.}}$

Rozwiązanie zależy $od$$poza$ spełniających nierówności $ale$ tym W tym zakresie funkcje i $displaystyle$$r}$ są określone przez

${\ Displaystyle f (\ rho) = - {\ sqrt {1-e ^ {- (2 \, m / n) \ fi}}} }$

I

${\ Displaystyle R (\ rho) = \ textstyle {\ sqrt {(\ rho -m) ^ {2} + a ^ {2}}}}$${\ Displaystyle e ^ {(m/n) \ phi} = {\ sqrt {\ Frac {(\ rho -m )^{2}+a^{2}}{1-f^{2}(\rho )}}}\,,}$

w którym

${\ Displaystyle \ phi = \ alfa (\ rho) = {\ Frac {n} {a}} \ lewo [ {\frac {\pi }{2}}-\tan ^{-1}\left({\frac {\rho -m}{a}}\right)\right]}$ i ${\ Displaystyle \; a = {\ sqrt {n ^ {2} -m ^ {2}}}.}$

Zakresy współrzędnych są

${\ Displaystyle - \ infty <t \,, T <\ infty \, \; \, - \ infty <\ rho < \infty \,,\;\;0<\vartheta <\pi \,,\;\;}$ i ${\ Displaystyle \; \, - \ pi <\ varphi <\ pi \,.}$

(Aby ułatwić porównanie z rozwiązaniem Schwarzschilda , oryginalne rozwiązanie zostało zastąpione przez $Displaystyle$$\ rho -m.$ )

Asymptotycznie, ponieważ ${\ Displaystyle \ rho \ do \ infty$ }

${\ Displaystyle \ alfa (\ rho) \ sim n / \ rho \ ,, \; \; r (\rho )\sim \rho \,,\;\;f(\rho )\sim -{\sqrt {2m/\rho }}\,,\;\;}$ i ${\ Displaystyle \; \; f ^ {2} (\ rho) \ sim 2m / \ rho \,.}$

Pokazują one, po porównaniu metryki odpływu z metryką Schwarzschilda

${\ Displaystyle {\ rozpocząć {wyrównane} c ^ {2} d \ tau ^ {2} & = c ^{2}dt^{2}-[d\rho -f_{\text{S}}(\rho )\,c\,dt]^{2}-r_{\text{S}}^{2 }(\rho )\,d\Omega ^{2}\\&=\left[1-f_{\text{S}}^{2}(\rho )\right]\,c^{2}\ ,dT^{2}-{\frac {1}{1-f_{\text{S}}^{2}(\rho )}}\,d\rho ^{2}-r_{S}^{ 2}(\rho )\,d\Omega ^{2}\,,\end{wyrównane}}}$

gdzie w jednostkach częściowo zgeometryzowanych ( ${\ displaystyle G = c}$ ) ,

${\ Displaystyle R _ {\ tekst {S}} (\ rho) = \ rho \ ,, \; \; f_ {\ tekst { S}} (\ rho) = - {\ sqrt {2M / \ rho}} \ , \; \;}$ i $\ Displaystyle \; \; f_ {\ tekst{S}}^{2}(\rho )=2M/\rho \,,}$

że parametr $jest$ odpowiednikiem otworu spustowego parametru $masy$

Z drugiej strony, jak ${\ Displaystyle \ rho \ do - \ infty$ }

${\ Displaystyle \ alfa (\ rho) \ sim n \ pi / a \ , \; \; r (\ rho )\sim -\rho e^{m\pi /a}\,,\;\;}$ i ${\ Displaystyle \; \; f ^ {2} (\ rho) \ sim 1-e ^ {- 2m \ pi / a} \,.}$

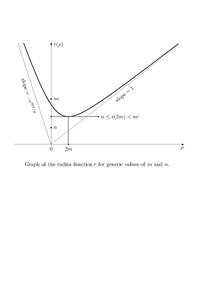
$ρ$ wykres przedstawia te asymptotyki, a także fakt, że odpowiadający (gdzie metryka Schwarzschilda ma swój notoryczny jednokierunkowy horyzont zdarzeń oddzielający $\ displaystyle \ rho = 2 M}$ ρ ${\ Displaystyle \ rho > 2 M}$ , z wnętrza czarnej dziury, gdzie $\ Displaystyle \ rho <2 M}$ ), ${\ Displaystyle r}$ osiąga ${ \ displaystyle \ rho = 2 m} dodatnia wartość minimalna,$$displaystyle \ rho >$ której „górny” region (gdzie ) otwiera się na bardziej przestronny „dolny” region (gdzie $} \displaystyle \rho <2m}$ ).

wykres ${\ displaystyle r}$

wykres ${\ displaystyle f ^ {2}}$

Przepływ eteru

Pole wektorowe $\ Displaystyle \ częściowe _ {t} + cf (\ rho) \ częściowe _ {\ rho}}$ generuje geodezję radialną sparametryzowaną przez właściwy czas ${\ displaystyle \ tau}$$,$ co zgadza się z czasem współrzędnych geodezji.

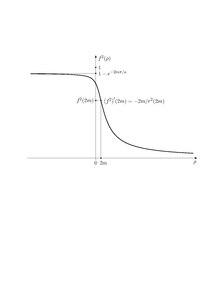
Jak można wywnioskować z wykresu $Displaystyle$ cząstka testowa podążająca za jedną z tych geodezji zaczyna od spoczynku w $rho = \ infty,}$ opada w dół w kierunku otwór odpływowy nabiera prędkości do końca, przechodzi przez otwór odpływowy i wychodzi do dolnego regionu, wciąż nabierając prędkości w kierunku do dołu, i dociera do ${\ Displaystyle \ rho = - \ infty}$ z

${\ Displaystyle \ operatorname {prędkość} = c | f (- \ infty) | = c {\ sqrt {1-e ^ {- 2 m \ pi / a}} <c.}$

Pole wektorowe, o którym mowa, jest polem prędkości mniej lub bardziej substancjalnego „eteru” przenikającego całą czasoprzestrzeń. Ten eter jest na ogół „czymś więcej niż zwykłym obojętnym ośrodkiem propagacji fal elektromagnetycznych; jest to niespokojne, płynne kontinuum, którego wewnętrzne, względne ruchy objawiają się nam jako grawitacja. Cząsteczki masy pojawiają się jako źródła lub pochłaniacze tego płynącego eteru. "

Dla geodezji czasoprzestrzennej w ogólności jest to radialne równanie ruchu

${\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {d ^ {2} \ rho} {d \ tau ^ {2}}} & = - \ lewo ({\ Frac {f ^ {2}} {2} }\right)^{\mathbf {\prime }}(\rho )+(\rho -3m)\left({\frac {d\Omega }{d\tau }}\right)^{2}\\ &=-{\frac {m}{r^{2}(\rho )}}+(\rho -3m)\left({\frac {d\Omega }{d\tau }}\right)^{ 2}\,.\end{wyrównane}}}$

Z tego widać, że

• to „rozciąganie” przepływu eteru mierzone terminem powoduje przyciąganie w dół ${\ Displaystyle - (f ^ {2}/2) '(\ rho)}$ grawitacji,
• każda badana cząstka, której orbita spadnie tak nisko, jak ${\ displaystyle \ rho = 3m}$ wpadnie przez otwór spustowy,
• istnieją cząstki testowe o wystarczającej prędkości kątowej ${\ Displaystyle | d \ Omega / d \ tau |}$ , aby zrównoważyć przyciąganie w dół, że ich orbity (w szczególności okrągłe) są ograniczone do części górnego regionu, gdzie ${\ Displaystyle \ rho > 3 m$ }
• przyciąganie w dół powoduje w górnym obszarze przyspieszenie w kierunku otworu odpływowego, a zatem przyciągającą grawitację, ale w dolnym obszarze przyspieszenie od otworu odpływowego, a więc odpychającą grawitację,
• ciągnięcie w dół osiąga maksimum, gdzie jest minimum, a mianowicie w „gardle $”$ odpływu, gdzie Displaystyle \ $}$
• jeśli $re$$d \ tau =0}$ Ω ) w dowolnym miejscu w przestrzeni. (Jest to szczególny przypadek niegrawitacyjnego otworu drenażowego znanego jako tunel czasoprzestrzenny Ellisa ).

Przejezdność

$, że$ w górnym obszarze bez prędkości radialnej ( bez wystarczającego kąta prędkość spada $otwór$ do dolnego regionu Nie tak jasne, ale mimo to prawdziwe jest to, że badana cząsteczka rozpoczynająca się od punktu w dolnym obszarze może z wystarczającą prędkością w górę przejść przez otwór odpływowy do górnego obszaru. W ten sposób otwór odpływowy jest „pokonywany” przez badane cząstki w obu kierunkach. To samo dotyczy fotonów.

Pełen katalog geodezji odpływu można znaleźć w artykule Ellisa.

Brak horyzontów i osobliwości; kompletność geodezyjna

Dla metryki ogólnej postaci metryki odpływu, gdzie polem prędkości jest ${\ Displaystyle \ częściowe _ {t} + cf (\ rho) \ częściowe _ {\ rho}}$ płynącego eteru, prędkości współrzędnych $} dla$$)$ wynoszą do ( $f (\$$)$ i dla z przepływem wszędzie ${\ Displaystyle f (\ rho)> -1}$ , tak że ${\ Displaystyle c (f (\ rho) + 1)> 0$ } fale świetlne walczące z przepływem eteru mogą zyskać grunt. Z drugiej strony, w miejscach, w których $mogą$$f (\ rho ) = -1}$ najwyżej wytrzymać (jeśli ) lub w inny sposób zostać zmiecionym w dół do miejsca, w którym zmierza eter (jeśli ). ${\ Displaystyle f (\ rho) <-1}$ ). (Sytuację tę żartobliwie opisuje: „Ludzie w lekkich kajakach powinni unikać eterycznych bystrzy”.)

Ta ostatnia sytuacja jest widoczna w metryce Schwarzschilda, gdzie ${\ Displaystyle \ textstyle f _ {\ tekst {S}} (\ rho) = - {\ sqrt {2M / \ rho} } \,}$ , czyli na $rho$ zdarzeń Schwarzschilda, gdzie $= \ rho = 2M}$ i mniej niż $ρ$ horyzontu, gdzie $\ Displaystyle \ rho <2M$ }

Natomiast w otworze spustowym ${\ Displaystyle \ textstyle f ^ {2} (\ rho) <1-e ^ {- 2 m \ pi / a} <1}$ i ${\ Displaystyle \ textstyle f (\ rho) = - \ lewo [f ^ {2} (\ rho) \ prawo] ^ {1/2}> -1}$ , dla każdej wartości , więc nigdzie nie ma horyzontu, po jednej stronie którego fale świetlne walczące z przepływem eteru nie mogą zdobyć $terenu$

Ponieważ

• ${\ displaystyle r}$ i ${\ displaystyle f}$ są zdefiniowane na całej linii rzeczywistej i
• ${\ displaystyle r}$ jest ograniczony od ${\ displaystyle 0}$ przez ${\ displaystyle r (2m)}$ i
• $f ^ {2}}$$\$${\ Displaystyle {\ sqrt {1-e ^ {- 2 m \ pi / a }}}}$ jest ograniczony od (o ),

metryka odpływu nie obejmuje ani „osobliwości współrzędnych”, gdzie ${\ Displaystyle 1-f ^ {2} (\ rho) \ do 0},$ ani „osobliwości geometrycznej”, gdzie ${ \displaystyle r(\rho )\to 0}$ , nawet asymptotyczne. Z tych samych powodów każda geodezja z nieograniczoną orbitą $infty$$}$ \ displaystyle . Kolektor ściekowy jest zatem geodezyjnie kompletny .

Siła odpychania

$cząstek$ przepływu eteru powoduje w górnym obszarze przyspieszenie w $jak$ z $\ rho$ identyfikuje jako $drenażowego$ masę grawitacyjną niezlokalizowanej cząstki $a}}$ formalnie takie samo, ale ponieważ asymptotyczne do $π$${\ Displaystyle - \ rho e ^ {m \$ zamiast $\ Displaystyle -\ rho}$$jak$ , nie wywnioskować, że odpychająca masa grawitacyjna cząstki otworu ściekowego wynosi $-m}$${\ Displaystyle -\$ .

Aby poznać odpychającą masę otworu spustowego, należy znaleźć izometrię kolektora otworu spustowego, która zamienia górne i dolne obszary. Taką izometrię można opisać w następujący sposób: Niech $¯$ kolektor odpływowy $którego$ M $,$ i ${\ Displaystyle M _ {{\ bar {m}}, {\ bar {n}}}}$ oznacza kolektor odpływowy, którego parametry są ${\ Displaystyle {\ bar {m}}}$ i ${\ Displaystyle {\bar {n}}}$ , gdzie

$\ Displaystyle {\ bar {m}} = - ja ^ {m \ pi / a}}$

I

${\ Displaystyle \; \; {\ bar {n}} = ne ^ {m \ pi / a}.}$

$\ Displaystyle$ punkt o z $}$ { m M ${\ Displaystyle M _ {{\ bar {m}}, {\ bar {n}}}}$ współrzędne ${\ Displaystyle [{\ bar {T}}, {\ bar {\ rho}}, {\ bar {\ vartheta}}, {\ bar { \varphi }}]=[Te^{-m\pi /a},-\rho e^{m\pi /a},\vartheta ,\varphi ]}$ . $}}} faktycznie ta sama rozmaitość$ z tego wywnioskować, że i M $, {$$\ do - \ rho}} \ do \ infty }$ że dolny region, w którym przebrany za górny region, w którym ${ \ Displaystyle \$ , ma $|$${\ Displaystyle \, | {\ bar {m}} |/| m | = - {\ bar {m.}}/m = e ^ {m \ pi /a}>1}$ silniej niż prawdziwy górny obszar je przyciąga, w stosunku .

Płaskość asymptotyczna

Że odpływ jest asymptotycznie płaski, jak $) \ sim \ rho}$ z asymptotycznego zachowania ${\ Displaystyle f ^ {2} (\ rho) \ sim 2m / \ rho \ sim 0.}$$\ Displaystyle r (\$ i Że jest asymptotycznie płaskie jak ${\ Displaystyle \ rho \ do - \ infty}$ widać na podstawie odpowiedniego zachowania jako $Displaystyle {\ bar {\ rho}} \ do \ infty}$${\ Displaystyle M _ {{\ bar {m}}, {\ bar {n}}}}$ po izometrii między $}}$ n opisane powyżej.

parametr n

$do$ parametru , $interpretowanego$ jako atrakcyjna masa grawitacyjna odpływu, parametr oczywistej interpretacji fizycznej. Zasadniczo ustala zarówno promień $,$ , który wzrasta od ${\ displaystyle n}$ gdy $\ displaystyle m = 0$ n $\ displaystyle ne}$ jak ${\ Displaystyle m \ do n,}$$n \ pi / 2}$ energia pola skalarnego $Displaystyle$ która maleje z gdy ${\ Displaystyle m = 0}$ do ${\ Displaystyle n/2}$ jak ${\ Displaystyle m \ do n}$ .

Z powodów podanych w ust. 6.1 artykułu z 2015 roku Ellis sugeruje, że $w jakiś sposób określa$ bezwładności cząstki modelowanej przez otwór spustowy. Pisze dalej, że „ higgsowskim ” sposobem wyrażenia tej idei jest stwierdzenie, że odpływ „nabiera” (bezwładności) masy z $skalarnego$ .

Aplikacja

Odrzucając nieuzasadnione założenie Einsteina z 1916 r., że masa bezwładna jest źródłem grawitacji, Ellis dochodzi do nowych, ulepszonych równań pola, których rozwiązaniem jest model kosmologiczny, który dobrze pasuje do obserwacji supernowych, które w 1998 r. ujawniły przyspieszenie rozszerzania się wszechświata . W tych równaniach występują dwa pola skalarne minimalnie sprzężone z geometrią czasoprzestrzenną o przeciwnych biegunach. „ $.$ kosmologiczna ” zostaje zastąpiona przez odpychającą gęstość netto materii grawitacyjnej, spowodowaną obecnością „tuneli” pierwotnych otworów drenażowych i ciągłym tworzeniem nowych tuneli, z których każdy ma nadmiar odpychania nad przyciąganiem Te tunele ściekowe związane z cząstkami widzialnej materii zapewniają ich grawitację; ci, którzy nie są związani z widoczną materią, to niewidzialna „ ciemna materia ”. „ Ciemna energia ” to odpychająca gęstość netto wszystkich tuneli ściekowych. Model kosmologiczny charakteryzuje się „ wielkim odbiciem ” zamiast „wielkiego wybuchu”, inflacyjnym przyspieszeniem wychodzącym z odbicia i płynnym przejściem do ery zwalniającego wybiegu, po którym ostatecznie następuje powrót do wykładniczej ekspansji de Sittera .

Dalsze zastosowania

• Tunel czasoprzestrzenny Ellis posłużył jako punkt wyjścia do budowy przejezdnego tunelu czasoprzestrzennego, który pojawił się w filmie Interstellar z 2014 roku (chociaż model, który został użyty w końcu, znacznie się różnił).
• Rozpraszanie przez tunel czasoprzestrzenny Ellis
• Soczewkowanie przestrzenne ( nie soczewkowanie grawitacyjne , ponieważ nie ma grawitacji) w tunelu czasoprzestrzennym Ellis
  • Mikrosoczewkowanie przez tunel czasoprzestrzenny Ellis
  • Efekt fali w soczewkowaniu przez tunel czasoprzestrzenny Ellis
  • Przemieszczenia środka ciężkości obrazu spowodowane mikrosoczewkowaniem przez tunel czasoprzestrzenny Ellis
  • Dokładne równanie soczewki dla tunelu czasoprzestrzennego Ellisa
  • Soczewkowanie przez tunele czasoprzestrzenne