Błąd o jeden

Błąd off-by-one lub off-by-one (znany pod akronimami OBOE , OBO , OB1 i OBOB ) to błąd logiczny obejmujący dyskretny odpowiednik warunku brzegowego . Często występuje w programowaniu komputerowym , gdy pętla iteracyjna iteruje o jeden raz za dużo lub za mało. Ten problem może powstać, gdy programista popełnia błędy, takie jak użycie „jest mniejsze niż lub równe”, gdzie „jest mniejsze niż” powinno być użyte w porównaniu, lub nie bierze pod uwagę, że sekwencja zaczyna się od zera, a nie od jednego ( jak w przypadku indeksów tablicowych w wielu językach). Może to również wystąpić w matematycznym .

Sprawy

Zapętlanie tablic

Rozważmy tablicę elementów, a elementy od m do n (włącznie) mają zostać przetworzone. Ile jest przedmiotów? Intuicyjna odpowiedź może brzmieć n − m , ale jest to różnica o jeden, co wskazuje na błąd słupka ogrodzenia ; prawidłowa odpowiedź to ( n – m ) + 1.

Z tego powodu zakresy w obliczeniach są często reprezentowane przez półotwarte przedziały ; zakres od m do n (włącznie) jest reprezentowany przez zakres od m (włącznie) do n + 1 (wyłącznie), aby uniknąć błędów słupków ogrodzeniowych. Na przykład pętlę , która iteruje pięć razy (od 0 do 4 włącznie), można zapisać jako półotwarty przedział od 0 do 5: 

   0     

    
 for  (  indeks  =  ;  indeks  <  5  ;  indeks  ++  )  {  /* Treść pętli */  }

Ciało pętli jest wykonywane najpierw z indeksem równym 0; indeks staje się wtedy 1, 2, 3 i ostatecznie 4 w kolejnych iteracjach. W tym momencie indeks staje się 5, więc indeks < 5 jest fałszywy i pętla się kończy. Jeśli jednak użyte porównanie było <= (mniejsze lub równe), pętla zostałaby wykonana sześć razy: indeks przyjmuje wartości 0, 1, 2, 3, 4 i 5. Podobnie, jeśli indeks zostałby zainicjowany na 1 zamiast 0, byłyby tylko cztery iteracje: index przyjmuje wartości 1, 2, 3 i 4. Obie te alternatywy mogą powodować błędy off-by-one.

Inny taki błąd może wystąpić, jeśli zamiast pętli while zostanie użyta pętla do-while (lub odwrotnie). Gwarantuje się, że pętla do-while zostanie wykonana co najmniej raz.

Zamieszanie związane z tablicami może również wynikać z różnic w językach programowania. Numeracja od 0 jest najbardziej powszechna, ale niektóre języki zaczynają numerację tablic od 1. Pascal ma tablice z indeksami zdefiniowanymi przez użytkownika. Umożliwia to modelowanie indeksów tablicy po domenie problemowej.

Błąd słupka ogrodzeniowego

Proste ogrodzenie o n odcinkach ma n +1 słupków.

Błąd słupka ogrodzeniowego ( czasami nazywany błędem słupa telegraficznego, latarni lub płotu ) jest specyficznym rodzajem błędu o jeden. Wczesny opis tego błędu pojawia się w pracach Witruwiusza . Poniższy problem ilustruje błąd:

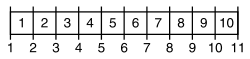
Jeśli zbudujesz proste ogrodzenie o długości 30 stóp ze słupkami oddalonymi od siebie o 3 stopy, ile słupków potrzebujesz?

Wspólna odpowiedź 10 postów jest błędna. Ta odpowiedź wynika z podzielenia długości ogrodzenia przez odległość od każdego słupka, przy czym iloraz jest błędnie klasyfikowany jako liczba słupków. W rzeczywistości ogrodzenie składa się z 10 sekcji i 11 słupków.

W tym scenariuszu ogrodzenie z n sekcjami będzie miało n + 1 słupków. I odwrotnie, jeśli ogrodzenie zawiera n słupków, będzie zawierało n − 1 sekcji. Ten związek jest ważny do rozważenia, gdy mamy do czynienia z błędem odwrotnym. Błąd odwrotny występuje, gdy znana jest liczba postów i zakłada się, że liczba sekcji jest taka sama. W zależności od konstrukcji ogrodzenia założenie to może być prawidłowe lub błędne.

Poniższy problem pokazuje błąd odwrotny:

Jeśli masz n postów, ile sekcji jest między nimi?

Interpretacja projektu ogrodzenia zmienia odpowiedź na ten problem. Prawidłowa liczba odcinków ogrodzenia to n − 1 , jeśli ogrodzenie jest wolnostojącym odcinkiem linii ograniczonym słupkami na każdym jego końcu ( np . wolnostojąca pętla (np. pomieszczenie dostępne po pokonaniu, takie jak ring bokserski) lub n + 1 jeśli słupki nie występują na końcach ogrodzenia przypominającego segment linii (np. ogrodzenie między dwoma budynkami i zakotwiczone w ścianie). Dokładna definicja problemu musi być starannie przemyślana, ponieważ konfiguracja dla jednej sytuacji może dać niewłaściwą odpowiedź dla innych sytuacji. Błędy słupków ogrodzeniowych wynikają z liczenia rzeczy, a nie odstępów między nimi lub odwrotnie, lub z zaniedbania rozważenia, czy należy policzyć jeden, czy oba końce rzędu.

Błędy słupków ogrodzeniowych mogą również wystąpić w jednostkach innych niż długość. Na przykład Piramida Czasu , składająca się ze 120 bloków umieszczonych w 10-letnich odstępach między blokami, ma zająć 1190 lat (nie 1200), od zainstalowania pierwszego bloku do ostatniego bloku. Jeden z najwcześniejszych błędów słupka ogrodzeniowego dotyczył czasu, w którym kalendarz juliański pierwotnie nieprawidłowo obliczał lata przestępne , z powodu liczenia włącznie, a nie wyłącznie, dając rok przestępny co trzy lata, a nie co cztery.

„Błąd słupka ogrodzeniowego” może w rzadkich przypadkach odnosić się do błędu spowodowanego nieoczekiwanymi regularnościami wartości wejściowych, które mogą (na przykład) całkowicie udaremnić teoretycznie wydajną implementację drzewa binarnego lub funkcji skrótu . Ten błąd dotyczy różnicy między oczekiwanym a najgorszym przypadkiem zachowania algorytmu .

W przypadku większej liczby, bycie poza jednym często nie jest poważnym problemem. Jednak w przypadku mniejszej liczby iw szczególnych przypadkach, w których dokładność jest najważniejsza, popełnienie błędu o jeden może być katastrofalne. Czasami taka kwestia również się powtórzy, a zatem pogorszy, gdy ktoś przekaże błędny rachunek, jeśli następna osoba ponownie popełni ten sam błąd (oczywiście błąd może być również odwrócony).

Przykład tego błędu może wystąpić w języku obliczeniowym MATLAB z funkcją interpolacji liniowej linspace() , której parametrami są ( wartość dolna , wartość górna , liczba wartości ) , a nie ( wartość dolna , wartość górna , liczba przyrostów ) . Programista, który błędnie rozumie trzeci parametr jako liczbę przyrostów, może mieć nadzieję, że linspace(0,10,5) uzyska sekwencję [0, 2, 4, 6, 8, 10] ale zamiast tego dostaniemy [0, 2.5, 5, 7.5, 10] .

Implikacje bezpieczeństwa

Częsty błąd off-by-one, który skutkuje błędem związanym z bezpieczeństwem, jest spowodowany niewłaściwym użyciem procedury strncat biblioteki standardowej C. Częstym nieporozumieniem związanym z strncat jest to, że gwarantowane zakończenie zerowe nie zapisze poza maksymalną długość. W rzeczywistości zapisze kończący znak null o jeden bajt poza określoną maksymalną długość. Poniższy kod zawiera taki błąd: 

    

     
     0 
       
 nieważne  foo  (  char  *  s  )  {  char  buf  [  15  ];  memset  (  buf  ,  ,  sizeof  (  buf  ));  strncat  (  buf  ,  s  ,  sizeof  (  buf  ));  // Końcowym parametrem powinno być: sizeof(buf)-1  }

Błędy off-by-one są powszechne w korzystaniu z biblioteki C, ponieważ nie jest to spójne w odniesieniu do tego, czy należy odjąć 1 bajt - funkcje takie jak fgets() i strncpy nigdy nie zapiszą poza podaną im długość ( fgets() odejmuje 1 się i pobiera tylko (długość − 1) bajtów), podczas gdy inne, takie jak strncat , będą zapisywać poza podaną im długość. Programista musi więc pamiętać, dla których funkcji musi odjąć 1.

W niektórych systemach ( w szczególności na architekturach little endian ) może to spowodować nadpisanie najmniej znaczącego bajtu wskaźnika ramki . Może to spowodować sytuację nadającą się do wykorzystania, w której osoba atakująca może przejąć zmienne lokalne dla procedury wywołującej.

Jednym z podejść, które często pomaga uniknąć takich problemów, jest użycie wariantów tych funkcji, które obliczają, ile należy zapisać na podstawie całkowitej długości bufora, a nie maksymalnej liczby znaków do zapisania. Takie funkcje obejmują strlcat i strlcpy i są często uważane za „bezpieczniejsze”, ponieważ ułatwiają uniknięcie przypadkowego zapisu poza końcem bufora. (W powyższym przykładzie kodu wywołanie tego strlcat(buf, s, sizeof(buf)) usunęłoby błąd.)

Zobacz też

Cytaty

Źródła

Dalsza lektura

  •   Parker, Matt (2021). Humble Pi: Kiedy matematyka idzie źle w prawdziwym świecie . Książki Riverheada. ISBN 978-0593084694 .
Pobrane z „ https://en.wikipedia.org/w/index.php?title=Off-by-one_error&oldid=1143042773 ”