paradoks Lindleya

Paradoks Lindleya to sprzeczna z intuicją sytuacja w statystyce , w której podejście bayesowskie i częstościowe do problemu testowania hipotez daje różne wyniki dla pewnych wyborów wcześniejszego rozkładu . Problem niezgodności między tymi dwoma podejściami został omówiony w podręczniku Harolda Jeffreysa z 1939 r.; stało się znane jako paradoks Lindleya po tym, jak Dennis Lindley nazwał ten spór paradoksem w artykule z 1957 roku.

Chociaż określane jako paradoks , różne wyniki z podejścia bayesowskiego i częstościowego można wyjaśnić raczej jako wykorzystanie ich do odpowiedzi na zasadniczo różne pytania, niż rzeczywistą niezgodę między tymi dwiema metodami.

Niemniej jednak dla dużej klasy przeorów różnice między podejściem częstości a podejściem bayesowskim wynikają z utrzymywania stałego poziomu istotności: jak zauważył nawet Lindley, „teoria nie usprawiedliwia praktyki utrzymywania stałego poziomu istotności”, a nawet „niektórzy obliczenia przeprowadzone przez prof. szybko, to rozbieżność między podejściem częstościowym a podejściem bayesowskim staje się nieistotna wraz ze wzrostem wielkości próby.

Opis paradoksu

Wynik $jakiegoś$ $}$ ma dwa możliwe wyjaśnienia, hipotezy i ${\ displaystyle \ textstyle H_$ oraz pewną wcześniejszą dystrybucję ${ \ displaystyle \ textstyle \ pi}$ reprezentujący niepewność co do tego, która hipoteza jest dokładniejsza przed wzięciem pod uwagę ${\ displaystyle \ textstyle x}$ .

Paradoks Lindleya występuje, gdy

Wynik jest „znaczący” w teście częstości , wskazującym na wystarczające dowody, aby odrzucić, $powiedzmy,$ { $x}$ $textstyle$ na poziomie 5%, oraz
Podane późniejsze prawdopodobieństwo $displaystyle \ textstyle x}$ $co wskazuje$ $H_ {0}$ mocne dowody na to, że lepiej zgadza się z $H$ $textstyle$ \ niż ${\ displaystyle \ textstyle H_ {1}}$ .

$,$ gdy jest bardzo specyficzny, bardziej rozproszony, a wcześniejsza dystrybucja nie faworyzuje silnie jednego $.$ inne, jak widać poniżej.

Przykład liczbowy

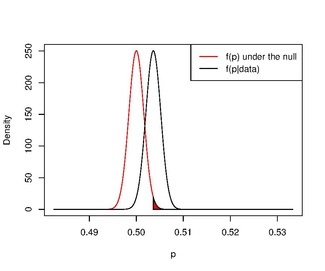
Poniższy przykład liczbowy ilustruje paradoks Lindleya. W pewnym mieście w pewnym okresie urodziło się 49 581 chłopców i 48 870 dziewczynek. Obserwowany odsetek $mężczyzn$ wynosi zatem 49 581/98 451 ≈ 0,5036. Zakładamy, że ułamek urodzeń chłopców jest zmienną dwumianową z parametrem ${\ displaystyle \ textstyle \ theta}$ . Jesteśmy zainteresowani sprawdzeniem, czy $wynosi$ , czy jakaś inna wartość. Oznacza to, że nasza hipoteza zerowa to ${\ Displaystyle \ textstyle H_ {0}: \ theta = 0,5}$ , a alternatywą jest ${\ Displaystyle \ textstyle H_ {1}: \ theta \ neq 0,5}$ .

Podejście frekwencjonistyczne

Częstym podejściem do testowania $jest$ obliczenie wartości p , prawdopodobieństwa zaobserwowania ułamka chłopców co najmniej tak dużego, jak $\ displaystyle \ textstyle x}$ przy założeniu, że ${\ displaystyle \ textstyle x} \textstyle H_{0}}$ jest prawdziwe. Ponieważ liczba urodzeń jest bardzo duża, możemy zastosować przybliżenie normalne dla ułamka urodzeń mężczyzn ${\ Displaystyle \ textstyle X \ sim N (\ mu, \ sigma ^ {2})}$ z ${\ Displaystyle \ textstyle \ mu = np = n\theta =98451\times 0,5=49225,5}$ i $obliczenia$ _

{\ Displaystyle {\ rozpocząć {wyrównane} P (X \ geq x \ mid \ mu = 49225,5) = \ int _ {x = 49581} ^ {98451} {\ Frac {1} {\ sqrt {2 \ pi \ sigma ^{2}}}}e^{-({\frac {u-\mu}}{\sigma}})^{2}/2}du\\=\int _{x=49581}^{98451} {\frac {1}{\sqrt {2\pi (24612,75)}}}e^{-{\frac {(u-49225.5)^{2}}{24612,75}}/2}du\około 0,0117.\ koniec {wyrównany}}}

Bylibyśmy równie zaskoczeni, gdybyśmy widzieli 49 581 urodzeń płci żeńskiej, tj $bywalca$ zwykle przeprowadzałby test dwustronny , dla którego wartość p wynosiłaby ${\ Displaystyle \ textstyle p \ około 2 \ razy 0,0117 = 0,0235}$ . W obu przypadkach wartość p jest niższa niż poziom istotności α wynoszący 5%, więc podejście częstości odrzuca ${\ displaystyle \ textstyle H_ {0}}$ ponieważ nie zgadza się z obserwowanymi danymi.

podejście bayesowskie

$, że$ bayesowskie polegałoby na przypisaniu $\ textstyle H_ {0} }}$ równomierny rozkład do poniżej $następnie$ obliczyć późniejsze prawdopodobieństwo $\ displaystyle$ za pomocą Twierdzenie Bayesa ,

{\ Displaystyle P (H_ {0} \ mid k) = {\ Frac {P (k \ mid H_ {0}) \ pi (H_ {0})} {P (k \ mid H_ {0}) \ pi (H_{0})+P(k\mid H_{1})\pi (H_{1})}}.}

Po zaobserwowaniu $chłopców$ z późniejsze prawdopodobieństwo $za$ funkcji zmienna dwumianowa,

{\ Displaystyle {\ rozpocząć {wyrównane} P (k \ mid H_ {0}) & = {n \ wybierz k} (0,5) ^ {k} (1-0,5) ^ {nk} \ około 1,95 \ razy 10 ^ {-4}\\P(k\mid H_{1})&=\int _{0}^{1}{n \choose k}\theta ^{k}(1-\theta )^{nk} d\theta ={n \wybierz k}\mathrm {\mathrm {B} } (k+1,n-k+1)=1/(n+1)\około 1,02\razy 10^{-5}\ koniec {wyrównany}}}

gdzie ${\ Displaystyle \ textstyle \ operatorname {\ operatorname {B}} (a, b)}$ jest funkcją Beta .

Na podstawie tych wartości znajdujemy późniejsze prawdopodobieństwo ${\ Displaystyle P (\ textstyle H_ {0} \ mid k) \ około 0,95}$ , co zdecydowanie faworyzuje ${\ Displaystyle \ textstyle H_ {0} }}$ nad ${\ displaystyle \ textstyle H_ {1}}$ .

Te dwa podejścia - bayesowskie i częstościowe - wydają się być w konflikcie i to jest „paradoks”.

Pogodzenie podejścia bayesowskiego i częstościowego

Prawie pewne testowanie hipotez

Naaman zaproponował dostosowanie poziomu istotności do liczebności próby w celu kontroli wyników fałszywie dodatnich: $α n$ , takie, że $α n = n - r$ gdzie $r > 1/2$ . Przynajmniej w przykładzie numerycznym przyjęcie $r = 1/2$ daje poziom istotności 0,00318, więc bywalca nie odrzuciłby hipotezy zerowej, co jest zgodne z podejściem bayesowskim.

Nieinformacyjne przeorki

Dystrybucja

p

przy hipotezie zerowej i dystrybucja a posteriori

p

.

Jeśli użyjemy nieinformacyjnego przeoru i przetestujemy hipotezę bardziej podobną do tej w podejściu częstościowym, paradoks zniknie.

$($ obliczymy _ $_$ _ tj. ${\ Displaystyle \ textstyle \ pi (\ theta \ in [0,1]) = 1}$ ), znajdujemy

{\ Displaystyle P (\ theta \ mid k, n) = \ operatorname {\ operatorname {B}} (k + 1, n-k + 1).}

Jeśli użyjemy tego do sprawdzenia prawdopodobieństwa, że noworodek z większym prawdopodobieństwem będzie chłopcem niż dziewczynką, tj. ${\ Displaystyle P (\ theta > 0,5 \ mid k, n)$ } znaleźliśmy

{\ Displaystyle \ int _ {0,5} ^ {1} \ operatorname {\ operatorname {B}} (49582,48871) \ około 0,983.}

Innymi słowy, jest bardzo prawdopodobne, że odsetek urodzeń płci męskiej przekroczy 0,5.

Żadna analiza nie daje bezpośredniego oszacowania wielkości efektu , ale obie można wykorzystać do określenia, na przykład, czy odsetek urodzeń chłopców prawdopodobnie przekroczy jakiś określony próg.

Brak rzeczywistego paradoksu

Pozorna niezgodność między tymi dwoma podejściami jest spowodowana kombinacją czynników. Po ${\ displaystyle \ textstyle H_ {1}$ , powyższe podejście częstości testuje bez odniesienia do $}$ . Podejście bayesowskie ocenia $jako$ alternatywę dla i stwierdza $, że pierwsze lepiej zgadza$ obserwacjami Dzieje się tak, ponieważ ta druga hipoteza jest znacznie bardziej rozproszona, ponieważ ${\ displaystyle \ textstyle \ theta}$ może znajdować się w dowolnym miejscu w ${\ displaystyle \ textstyle [0,1]}$ , co powoduje, że ma bardzo niskie prawdopodobieństwo późniejsze. Aby zrozumieć dlaczego, pomocne jest rozważenie dwóch hipotez jako generatorów obserwacji:

Pod $,$ wybieramy i pytamy $.$ że zobaczymy 49 581 chłopców w 98 451
Pod , wybieramy $.$ $od 0$ 1 i zadajemy to samo pytanie

$Większość$ możliwych wartości $jest$ bardzo słabo obserwacjami Zasadniczo pozorna niezgodność między metodami wcale nie jest niezgodą, ale raczej dwoma różnymi stwierdzeniami dotyczącymi tego, w jaki sposób hipotezy odnoszą się do danych:

Bywalca stwierdza, że $jest$ słabe wyjaśnienie obserwacji.
Bayesian stwierdza, że jest to znacznie lepsze wyjaśnienie obserwacji niż ${1}$ ${\ displaystyle \ textstyle H_$ .

Stosunek płci noworodków wynosi nieprawdopodobnie 50/50 płci męskiej i żeńskiej, zgodnie z testem częstości. Jednak 50/50 jest lepszym przybliżeniem niż większość innych wskaźników, ale nie wszystkie . Hipoteza pasowałaby do obserwacji znacznie lepiej niż prawie wszystkie inne wskaźniki, w tym $0,500}$ 0,504 $około$

Na przykład ten wybór hipotez i wcześniejszych prawdopodobieństw implikuje stwierdzenie: „jeśli $\ displaystyle \ textstyle \ theta}$ ${$ > 0,49 i $theta}$ $\ displaystyle \ textstyle \ theta}$ < 0,51, to wcześniejsze prawdopodobieństwo równe 0,5 to 0,50/0,51 ${\ Displaystyle \ około}$ 98%. Biorąc pod $\ displaystyle \$ tak silną preferencję dla , łatwo zrozumieć, dlaczego podejście bayesowskie faworyzuje $theta = 0,5 } .$ w obliczu $Displaystyle x \ około 0,5036}$ $\$ , mimo że obserwowana wartość 2,28 $\ Displaystyle 2,28 \ sigma}$ od 0,5. Odchylenie o ponad 2 sigma od $.$ uważane za znaczące w podejściu częstościowym, ale jego znaczenie jest unieważniane przez przeor w podejściu bayesowskim

$w$ to z innej strony, możemy zobaczyć, że poprzedni rozkład jest zasadniczo płaski z delta Oczywiście jest to wątpliwe. W rzeczywistości, gdybyś miał wyobrazić sobie liczby rzeczywiste jako ciągłe, bardziej logiczne byłoby założenie, że żadna dana liczba nie byłaby dokładnie taką samą wartością parametru, tj. powinniśmy założyć, że P $\ styl wyświetlania P(\theta =0,5)=0}$ .

Bardziej realistyczny rozkład dla w alternatywnej $hipotezie$ daje mniej zaskakujący wynik dla tylnej części $textstyle H_ {0}}$ . Na przykład, jeśli zastąpimy ${\ displaystyle \ textstyle H_ {1}}$ przez ${\ displaystyle \ textstyle H_ {2}: \ theta = x}$ , tj. oszacowanie maksymalnego prawdopodobieństwa dla ${ \displaystyle\textstyle\theta}$ , późniejsze prawdopodobieństwo wyniosłoby tylko 0,07 w porównaniu do 0,93 dla (Oczywiście $nie$ faktycznie używać MLE jako części ${\ displaystyle \ textstyle H_ {2}}$ wcześniejsza dystrybucja).