Boole'owskie pitagorejskie zadanie trójek

Boolowski problem trójek pitagorejskich to problem z teorii Ramseya dotyczący tego, czy dodatnie liczby całkowite można pokolorować na czerwono i niebiesko, tak aby żadna trójka pitagorejska nie składała się wyłącznie z czerwonych lub wszystkich niebieskich elementów. Boolowski problem trójek pitagorejskich został rozwiązany przez Marijna Heule'a , Olivera Kullmanna i Victora W. Marka w maju 2016 r. za pomocą dowodu wspomaganego komputerowo .

Oświadczenie

Problem polega na tym, czy możliwe jest pokolorowanie każdej z dodatnich liczb całkowitych na czerwono lub niebiesko, tak aby żadna pitagorejska trójka liczb całkowitych za , b , do , spełniająca za $\ Displaystyle a ^ {2} + b^{2}=c^{2}}$ są tego samego koloru.

Na przykład w trójce pitagorejskiej 3, 4 i 5 ( ${\ Displaystyle 3 ^ {2} + 4 ^ {2} = 5 ^ {2}} )$ , jeśli 3 i 4 są kolorowe czerwony, to 5 musi być w kolorze niebieskim.

Rozwiązanie

Marijn Heule , Oliver Kullmann i Victor W. Marek wykazali, że takie pokolorowanie jest możliwe tylko do liczby 7824. Właściwym stwierdzeniem udowodnionego twierdzenia jest

Twierdzenie — Zbiór {1, . . . , 7824} można podzielić na dwie części, tak że żadna część nie zawiera trójki pitagorejskiej, podczas gdy jest to niemożliwe dla {1, . . . , 7825}.

Istnieje 2 ⁷⁸²⁵ ≈ 3,63 × 10 ²³⁵⁵ możliwych kombinacji kolorowania dla liczb do 7825 . Te możliwe kolorowania zostały logicznie i algorytmicznie zawężone do około biliona (nadal bardzo złożonych) przypadków, a te zostały zbadane za pomocą spełnialności Boole'a . Stworzenie dowodu zajęło około 4 lat obliczeniowych obliczeń w ciągu dwóch dni na superkomputerze Stampede w Texas Advanced Computing Center i wygenerowało 200-terabajtowy dowód propozycjonalny, który został skompresowany do 68 gigabajtów.

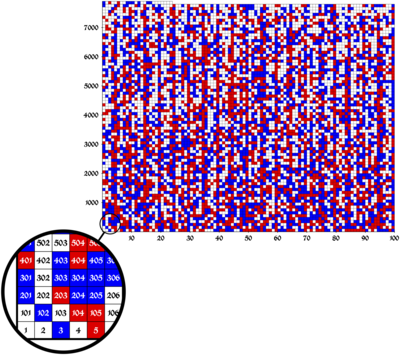
Artykuł opisujący dowód został opublikowany na konferencji SAT 2016, gdzie zdobył nagrodę dla najlepszego artykułu. Poniższy rysunek przedstawia możliwą rodzinę kolorowań dla zbioru {1,...,7824} bez monochromatycznej pitagorejskiej trójki, a białe kwadraty mogą być pokolorowane na czerwono lub niebiesko, jednocześnie spełniając ten warunek.

Nagroda

W latach 80. Ronald Graham za rozwiązanie problemu wyznaczył nagrodę w wysokości 100 dolarów, którą teraz otrzymał Marijn Heule .

Uogólnienia

Od 2018 r. Problem jest nadal otwarty dla więcej niż 2 kolorów, to znaczy, jeśli istnieje k -kolorowanie ( k ≥ 3) dodatnich liczb całkowitych, tak że żadna pitagorejska trójka nie ma tego samego koloru.

Zobacz też

Lista długich dowodów matematycznych

^ ^a ^b Baranek, Evelyn (26 maja 2016). „Dwustu terabajtowy dowód matematyczny jest największy w historii” . Natura . 534 (7605): 17–18. Bibcode : 2016Natur.534...17L . doi : 10.1038/natura.2016.19990 . PMID 27251254 .
^ ^ab ^Heule , Marijn JH; Kullmann, Oliver; Marek, Wiktor W. (2016). „Rozwiązywanie i weryfikowanie boolowskiego problemu trójek pitagorejskich za pomocą metody Cube-and-Conquer”. W Creignou, Nadia; Le Berre, Daniel (red.). Theory and Applications of Satisfiability Testing – SAT 2016: 19th International Conference, Bordeaux, Francja, 5-8 lipca 2016 r., Proceedings . Notatki z wykładów z informatyki. Tom. 9710. s. 228–245. ar Xiv : 1605.00723 . doi : 10.1007/978-3-319-40970-2_15 .
^ SOBOTA 2016
^ Eliahou, Szalom; Fromentin, Jean; Marion-Poty, Wirginia; Robiliard, Denis (2018-10-02). „Czy monochromatyczne trójki pitagorejskie są nieuniknione w przypadku kolorowania morficznego?” . Matematyka eksperymentalna . 27 (4): 419–425. ar Xiv : 1605.00859 . doi : 10.1080/10586458.2017.1306465 . ISSN 1058-6458 . S2CID 19035265 .

[nature-1] Baranek, Evelyn (26 maja 2016). „Dwustu terabajtowy dowód matematyczny jest największy w historii” . Natura . 534 (7605): 17–18. Bibcode : 2016Natur.534...17L . doi : 10.1038/natura.2016.19990 . PMID 27251254 .

[arXiv-2] Heule , Marijn JH; Kullmann, Oliver; Marek, Wiktor W. (2016). „Rozwiązywanie i weryfikowanie boolowskiego problemu trójek pitagorejskich za pomocą metody Cube-and-Conquer”. W Creignou, Nadia; Le Berre, Daniel (red.). Theory and Applications of Satisfiability Testing – SAT 2016: 19th International Conference, Bordeaux, Francja, 5-8 lipca 2016 r., Proceedings . Notatki z wykładów z informatyki. Tom. 9710. s. 228–245. ar Xiv : 1605.00723 . doi : 10.1007/978-3-319-40970-2_15 .

[3] SOBOTA 2016

[4] Eliahou, Szalom; Fromentin, Jean; Marion-Poty, Wirginia; Robiliard, Denis (2018-10-02). „Czy monochromatyczne trójki pitagorejskie są nieuniknione w przypadku kolorowania morficznego?” . Matematyka eksperymentalna . 27 (4): 419–425. ar Xiv : 1605.00859 . doi : 10.1080/10586458.2017.1306465 . ISSN 1058-6458 . S2CID 19035265 .