Planarna SAT

Przykład planarnego problemu SAT. Czarne krawędzie odpowiadają zmiennym nieodwróconym, a czerwone krawędzie odpowiadają zmiennym odwróconym.

W informatyce planarny problem spełnialności 3 (w skrócie PLANAR 3SAT lub PL3SAT ) jest rozszerzeniem klasycznego problemu Boole'a 3-spełnialności na planarny wykres częstości . Inaczej mówiąc, zadaje pytanie, czy zmienne danej formuły logicznej, której wykres częstości występowania składający się ze zmiennych i klauzul można osadzić na płaszczyźnie , można konsekwentnie zastąpić wartościami PRAWDA lub FAŁSZ w taki sposób, że formuła przyjmie wartość PRAWDA . W takim przypadku formułę nazywa się spełnialną . Natomiast jeżeli takiego przypisania nie ma, to funkcja wyrażona wzorem jest FALSE dla wszystkich możliwych przypisań zmiennych i wzór jest niespełnialny . Na przykład formuła „ a ORAZ NIE b ” jest spełnialna, ponieważ można znaleźć wartości a = PRAWDA i b = FAŁSZ, co daje ( a I NIE b ) = PRAWDA. Natomiast „ a ORAZ NIE a " jest niezadowalające.

Podobnie jak 3SAT , PLANAR-SAT jest NP-kompletny i jest powszechnie stosowany w redukcjach .

Definicja

Każdy problem 3SAT można przekonwertować na wykres częstości występowania w następujący sposób: dla każdej zmiennej $displaystyle v_ {i}$ ma jeden odpowiadający węzeł dla każdej klauzuli v ja ${$ ${\ displaystyle c_ {j}}$ , wykres ma jeden odpowiedni węzeł ${\ Displaystyle c_ {j}.}$ Krawędź ${\ displaystyle (v_ {i}, c_ {j})}$ jest tworzona pomiędzy zmienną $}$ $}$ $c_ {j$ i i klauzula do $}$ $displaystyle c_ {j}}$ kiedykolwiek jest w \ Literały dodatnie i ujemne rozróżnia się za pomocą kolorowania krawędzi .

Formuła jest spełnialna wtedy i tylko wtedy, gdy każdemu węzłowi zmiennej można przypisać PRAWDĘ lub FAŁSZ w taki sposób, że każdy węzeł klauzuli jest połączony z co najmniej jednym węzłem PRAWDA za pomocą dodatniej krawędzi lub FAŁSZ za pomocą ujemnej krawędzi.

Wykres planarny to graf, który można narysować na płaszczyźnie w taki sposób, aby żadne dwie jego krawędzie się nie przecinały. Planarny 3SAT jest podzbiorem 3SAT, w którym wykres częstości występowania zmiennych i klauzul formuły logicznej jest planarny. Jest to ważne, ponieważ jest to wariant ograniczony i nadal jest NP-kompletny. Wiele problemów (na przykład gry i łamigłówki) nie może przedstawić grafów niepłaskich. Dlatego Planar 3SAT umożliwia udowodnienie, że te problemy są NP-trudne.

Dowód NP-zupełności

Lewa strona to skrzyżowanie; prawa strona to gadżet crossover. Małe kropki oznaczają klauzule. Czarne i czerwone krawędzie odpowiadają odpowiednio zmiennym nieodwróconym i odwróconym.

Poniższy szkic dowodowy podąża za dowodem D. Lichtensteina.

Trywialnie, PLANAR 3SAT jest w NP . Wystarczy zatem pokazać, że jest on NP-trudny poprzez redukcję z 3SAT .

Dowód ten wykorzystuje fakt, że ${\ displaystyle (\ lnot a \ lnot b \ lnot b \ lor c) \ ziemia ( a\lor \lnot c)\land (b\lor \lnot c)}$ jest równoważne ${\ displaystyle (a \ land b) \ Leftrightarrow c}$ i to ${\ Displaystyle (a \ lub \ lnie b) \ ziemia (\ lnie a \ lor b)}$ jest równoważne ${\ displaystyle a \ Leftrightarrow b}$ .

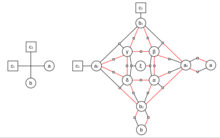
Najpierw narysuj wykres częstości występowania wzoru 3SAT. Ponieważ nie są ze sobą połączone żadne dwie zmienne ani klauzule, powstały wykres będzie dwudzielny . Załóżmy, że powstały wykres nie jest planarny. Dla każdego przecięcia krawędzi ( a , c ₁ ) i ( b , c ₂ ) wprowadź dziewięć nowych zmiennych a ₁ , b ₁ , α , β , γ , δ , ξ , a ₂ , b ₂ i zastąp każde skrzyżowanie krawędzi gadżetem crossover pokazanym na schemacie. Zawiera on następujące nowe klauzule:

{\ Displaystyle {\ początek {tablica} {ll} (\ lnie a_ {2} \ lo \ lnot b_ {2} \ lor \ alfa) \ ziemia (a_ {2} \ lub \ lnot \ alfa) \ lor (b_ {2}\lor \lnot \alpha ),&\quad {\text{ie,}}\quad a_{2}\land b_{2}\Leftrightarrow \alpha \\(\lnot a_{2}\lor b_ {1}\lor \beta )\land (a_{2}\lor \lnot \beta )\lor (\lnot b_{1}\lor \lnot \beta )&\quad {\text{ie,}} \quad a_{2}\land \lnot b_{1}\Leftrightarrow \beta \\(a_{1}\lor b_{1}\lor \gamma )\land (\lnot a_{1}\lor \lnot \ gamma )\lor (\lnot b_{1}\lor \lnot \gamma ),&\quad {\text{ie,}}\quad \lnot a_{1}\land \lnot b_{1}\Leftrightarrow \gamma \\(a_{1}\lor \lnot b_{2}\lor \delta )\land (\lnot a_{1}\lor \lnot \delta )\lor (b_{2}\lor \lnot \delta ) ,&\quad {\text{ie,}}\quad \lnot a_{1}\land b_{2}\Leftrightarrow \delta \\(\alpha \lor \beta \lor \xi )\land (\gamma \ lor \delta \lor \lnot \xi ),&\quad {\text{ie,}}\quad \alpha \lor \beta \lor \gamma \lor \delta \\(\lnot \alpha \lor \lnot \ beta )\land (\lnot \beta \lor \lnot \gamma )\land (\lnot \gamma \lor \lnot \delta )\land (\lnot \delta \lor \lnot \alpha )&\\(a_ {2}\lor \lnot a)\land (a\lor \lnot a_{2})\land (b_{2}\lor \lnot b)\land (b\lor \lnot b_{2}),& \quad {\text{ie,}}\quad a\Leftrightarrow a_{2},~b\Leftrightarrow b_{2}\\\end{array}}}

Jeśli krawędź ( a , c ₁ ) jest odwrócona na oryginalnym wykresie, ( a ₁ , c ₁ ) powinna zostać odwrócona w gadżecie crossover. Podobnie, jeśli krawędź ( b , c ₂ ) jest odwrócona w oryginale, ( b ₁ , c ₂ ) powinna zostać odwrócona.

Można łatwo wykazać, że klauzule te są spełnialne wtedy i tylko wtedy, gdy ${1}}$ 1 $b_$ \

Algorytm ten pokazuje, że możliwe jest przekształcenie każdego przejścia w jego planarny odpowiednik przy użyciu jedynie stałej ilości nowych dodatków. Ponieważ liczba skrzyżowań jest wielomianem pod względem liczby klauzul i zmiennych, redukcja jest wielomianem.

Warianty i problemy z nimi związane

Planarny 3SAT ze zmiennym cyklem : Tutaj, oprócz wykresu częstości, wykres zawiera również cykl przechodzący przez wszystkie zmienne, a każda klauzula znajduje się wewnątrz lub na zewnątrz tego cyklu. Powstały wykres musi być nadal planarny. Problem ten jest NP-zupełny.
- Jeśli jednak problem zostanie dodatkowo ograniczony w taki sposób, że wszystkie klauzule znajdują się w cyklu zmiennym lub wszystkie klauzule znajdują się poza nim, wówczas problem można rozwiązać w czasie wielomianowym za pomocą programowania dynamicznego .
Planarny 3SAT z literałami : dwudzielny wykres częstości występowania literałów i klauzul jest również planarny. Problem ten jest NP-zupełny.
Planarny prostoliniowy 3SAT : Wierzchołki wykresu są reprezentowane jako segmenty poziome. Każda zmienna leży na x , natomiast każda klauzula leży powyżej/poniżej osi x . Każde połączenie między zmienną a klauzulą musi być segmentem pionowym. Każda klauzula może mieć maksymalnie 3 połączenia ze zmiennymi i może być całkowicie dodatnia lub całkowicie ujemna. Problem ten jest NP-zupełny.
- Planarny monotoniczny prostoliniowy 3SAT : Jest to wariant planarnego prostoliniowego 3SAT, w którym klauzule powyżej x -oś są całkowicie dodatnie, a klauzule poniżej osi x są całkowicie ujemne. Problem ten jest NP-zupełny.
Planarny 1-w-3SAT : Jest to planarny odpowiednik 1-w-3SAT . Jest NP-zupełny.
- Planarny dodatni prostoliniowy 1-w-3SAT : Jest to planarny odpowiednik dodatniego 1-w-3SAT . Jest NP-zupełny.
Planarny NAE 3SAT : Ten problem jest planarnym odpowiednikiem NAE 3SAT . W przeciwieństwie do pozostałych wariantów, problem ten można rozwiązać w czasie wielomianowym . Dowód polega na redukcji do maksymalnego cięcia płaskiego .
Obwód planarny SAT : Jest to wariant obwodu SAT , w którym obwód obliczający wzór SAT jest planarnie skierowanym grafem acyklicznym . Należy pamiętać, że jest to inny wykres niż wykres sąsiedztwa formuły. Problem ten jest NP-zupełny.

Redukcje

Zagadki logiczne

Redukcja z Planar SAT jest powszechnie stosowaną metodą w dowodach NP-zupełności zagadek logicznych. Przykładami są Fillomino , Nurikabe , Shakashaka , Tatamibari i Tentai Show . Dowody te obejmują konstruowanie gadżetów, które mogą symulować przewody przenoszące sygnały (wartości logiczne), bramki wejściowe i wyjściowe, rozdzielacze sygnału, bramki NOT i bramki AND (lub OR) w celu przedstawienia płaskiego osadzania dowolnego obwodu Boole'a. Ponieważ obwody są płaskie, nie trzeba brać pod uwagę skrzyżowania przewodów.

Składanie na płasko łańcuchów o stałym kącie

Jest to problem ustalenia, czy łańcuch wielokątny o stałych długościach krawędzi i kątach ma konfigurację płaską bez skrzyżowań. Udowodniono, że jest silnie NP-twardy poprzez redukcję z płaskiego monotonicznego prostoliniowego 3SAT.

Przegroda o minimalnej długości krawędzi

Jest to problem podziału wielokąta na prostsze wielokąty, tak aby całkowita długość wszystkich krawędzi użytych w podziale była jak najmniejsza.

Gdy figura jest wielokątem prostoliniowym i należy ją podzielić na prostokąty, a wielokąt jest pozbawiony dziur, wówczas problemem jest wielomian. Jeśli jednak zawiera dziury (nawet dziury zdegenerowane – pojedyncze punkty), problem jest NP-trudny w wyniku redukcji z Planar SAT. To samo dotyczy sytuacji, gdy figura jest dowolnym wielokątem i należy ją podzielić na figury wypukłe.

Powiązanym problemem jest triangulacja minimalnej wagi - znalezienie triangulacji minimalnej całkowitej długości krawędzi. Udowodniono, że decyzyjna wersja tego problemu jest NP-zupełna poprzez redukcję z wariantu Planarnego 1-w-3SAT.