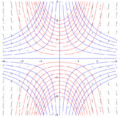
Pole zbocza

Pole

_

_

{\ Displaystyle {\ Frac {x ^ {3}} {3}} - {\ Frac {x ^ {2}} {2}} -2x + 4}

,

{\ Displaystyle {\ Frac {x ^ {3}} {3}} - {\ Frac {x ^ {2}} {2}} -2x}

i

{ \ Displaystyle {\ Frac {x ^ {3}} {3}} - {\ Frac {x ^ {2}} {2}} -2x-4}

odpowiednio.

Pola nachylenia (zwane także polami kierunkowymi ) są graficzną reprezentacją rozwiązań równania różniczkowego pierwszego rzędu funkcji skalarnej. Rozwiązania pola nachylenia to funkcje narysowane jako pełne krzywe. Pole nachylenia pokazuje nachylenie równania różniczkowego w określonych odstępach pionowych i poziomych na płaszczyźnie xy i może być użyte do określenia przybliżonego nachylenia stycznej w punkcie na krzywej, gdzie krzywa jest pewnym rozwiązaniem równania różniczkowego.

Definicja

Standardowy przypadek

Pole nachylenia można zdefiniować dla następujących typów równań różniczkowych

{\ Displaystyle y '= f (x, y)}

co można interpretować geometrycznie jako nachylenie stycznej do wykresu rozwiązania równania różniczkowego ( krzywej całkowej ) w każdym punkcie ( x , y ) w funkcji współrzędnych punktu.

$to postrzegać jako kreatywny sposób$ rzeczywistych dwóch zmiennych obrazu W szczególności dla danej pary rysowany jest wektor ze składowymi $\ Displaystyle$ $}$ punkt ${\ displaystyle x, y}$ na ${\ displaystyle x, y}$ -płaszczyzna. $znormalizowany$ wektor fabuła $jest$ zestaw par tworzących siatkę.

Izoklina (seria linii o tym samym nachyleniu) jest często używana do uzupełnienia pola nachylenia . ${\ Displaystyle y' = f (x, y)}$ fa , izoklina jest linią na płaszczyźnie przez ${\ Displaystyle x, y}$ ustawienie równe stałej ${\ Displaystyle f (x, y)} .$

Ogólny przypadek układu równań różniczkowych

Biorąc pod uwagę układ równań różniczkowych,

{\ Displaystyle {\ rozpocząć {wyrównane} {\ Frac {dx_ {1}}} {dt}} & = f_ {1} (t, x_ {1}, x_{2},\ldots,x_{n})\\{\frac {dx_{2}}{dt}}&=f_{2}(t,x_{1},x_{2},\ldots, x_{n})\\&\;\;\vdots \\{\frac {dx_{n}}{dt}}&=f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{wyrównane}}}

pole nachylenia jest tablicą znaków nachylenia w przestrzeni fazowej (w dowolnej liczbie wymiarów w zależności od liczby odpowiednich zmiennych; na przykład dwa w przypadku liniowego ODE pierwszego rzędu , jak widać po prawej). $_$ punkcie _ do wektora

{\ Displaystyle {\ rozpocząć {pmatrix} 1 \\ f_ {1} (t, x_ {1}, x_ {2}, \ ldots, x_ {n}) \\ f_ {2} (t, x_ {1} ,x_{2},\ldots ,x_{n})\\\vdots \\f_{n}(t,x_{1},x_{2},\ldots ,x_{n})\end{pmatrix} }.}

Liczba, pozycja i długość znaków nachylenia może być dowolna. Pozycje są zwykle wybierane w taki sposób, aby punkty $tworzyły$ a jednolita siatka. Opisany powyżej przypadek standardowy reprezentuje ${\ displaystyle n = 1}$ . Ogólny przypadek pola nachylenia dla układów równań różniczkowych nie jest łatwy do wizualizacji dla ${\ displaystyle n> 2}$ .

Aplikacja ogólna

Dzięki komputerom skomplikowane pola nachylenia można szybko tworzyć bez nudy, dlatego dopiero niedawno praktycznym zastosowaniem jest ich użycie jedynie w celu wyczucia, jakie powinno być rozwiązanie, zanim zostanie poszukane wyraźne rozwiązanie ogólne. Oczywiście komputery mogą również po prostu rozwiązać jeden, jeśli istnieje.

Jeśli nie ma wyraźnego ogólnego rozwiązania, komputery mogą używać pól nachylenia (nawet jeśli nie są pokazane), aby numerycznie znaleźć rozwiązania graficzne. Przykładami takich procedur są metoda Eulera lub lepiej metody Runge-Kutty .

Oprogramowanie do wykreślania pól nachylenia

Różne pakiety oprogramowania mogą kreślić pola nachylenia.

Kod pola kierunku w GNU Octave / MATLAB

                                
                      
                              
      funn  =  @(  x  ,  y  )  y  -  x  ;  % funkcja f(x, y) = yx  [  x  ,  y  ]  =  meshgrid  (  -  5  :  0,5  :  5  ); % przedziałów dla   nachyleń  x i y  =  funn  (  x  ,  y  );  % macierz wartości nachylenia  dy  =  nachylenia  ./  sqrt  (  1  +              
        
                       
 zbocza  .^  2  );  % normalizuje element liniowy...  dx  =  jedynki  (  długość  (  dy  ))  ./  sqrt  (  1  +  nachylenia  .^  2  );  % ...wielkości dla dy i dx  h  =  kołczan  (  x  ,  y  ,  dx  ,  dy  ,  0.5  ); % wykreśl   zestaw  pól kierunku  (  h  ,                        "maksymalny rozmiar głowy"  ,  0,1  );  % zmienić rozmiar głowy

Przykładowy kod dla Maxima

/* pole dla y'=xy (kliknij punkt, aby uzyskać krzywą całkową). Plotdf wymaga Xmaxima */ plotdf(x*y, [x,-2,2], [y,-2,2]);

Przykładowy kod dla Mathematica


 (* pole dla y'=xy *)  VectorPlot  [{  1  ,  x  *  y  -5  x  },{  x  ,  -2  ,  2  }, {  y  ,  -2  ,  2  }]

Przykładowy kod dla SageMath

var('x,y') plot_slope_field(x*y, (x,-2,2), (y,-2,2))

Przykłady

y' = x/y
Pole zbocza
Krzywe całkowe
Izokliny (niebieski), pole nachylenia (czarny) i niektóre krzywe rozwiązania (czerwony)

Zobacz też

Blanchard, Paweł; Devaney, Robert L .; i Hall, Glen R. (2002). Równania różniczkowe (wyd. 2). Brooks/Cole: Thompson Learning. ISBN 0-534-38514-1

Linki zewnętrzne