Zajęty bóbr

W informatyce teoretycznej gra w zajętego bobra ma na celu znalezienie programu kończącego o danym rozmiarze, który generuje jak najwięcej danych wyjściowych. Ponieważ który zapętla się w nieskończoność i generuje nieskończone wyniki, jest łatwy do pomyślenia, takie programy są wykluczone z gry.

Mówiąc dokładniej, gra pracowitego bobra polega na zaprojektowaniu zatrzymującej się maszyny Turinga z alfabetem {0,1}, która zapisuje najwięcej jedynek na taśmie, używając tylko zadanego zestawu stanów. Zasady gry dwustanowej są następujące:

maszyna musi mieć dwa stany oprócz stanu zatrzymania, oraz
taśma początkowo zawiera tylko zera.

Gracz powinien wymyślić tabelę przejściową, której celem jest uzyskanie najdłuższego wyjścia 1s na taśmie, jednocześnie upewniając się, że maszyna w końcu się zatrzyma.

N - ty zapracowany bóbr , BB- n lub po prostu „pracowity bóbr” to maszyna Turinga, która wygrywa grę zapracowanego bobra w stanie n . Oznacza to, że osiąga największą liczbę jedynek spośród wszystkich innych możliwych współzawodniczących maszyn Turinga w stanie n . Na przykład maszyna Turinga BB-2 osiąga cztery jedynki w sześciu krokach.

Ustalenie, czy dowolna maszyna Turinga jest pracowitym bobrem, jest nierozstrzygalne . Ma to wpływ na teorię obliczalności , problem zatrzymania i teorię złożoności . Pojęcie to zostało po raz pierwszy wprowadzone przez Tibora Radó w jego artykule z 1962 roku „O funkcjach nieobliczalnych”.

Gra

Gra w ruchliwego bobra w stanie n (lub gra BB- n ), przedstawiona w artykule Tibora Radó z 1962 r., obejmuje klasę maszyn Turinga , z których każdy element musi spełniać następujące specyfikacje projektowe:

Maszyna ma n stanów „operacyjnych” plus stan Zatrzymania, gdzie n jest dodatnią liczbą całkowitą, a jeden z n stanów wyróżnia się jako stan początkowy. (Zazwyczaj stany są oznaczone przez 1, 2, ..., n , ze stanem 1 jako stanem początkowym lub przez A , B , C , ..., ze stanem A jako stanem początkowym).
Maszyna wykorzystuje pojedynczą dwukierunkową nieskończoną (lub nieograniczoną) taśmę.
Alfabet taśmy to {0, 1}, gdzie 0 służy jako pusty symbol.
Funkcja przejścia maszyny przyjmuje dwa dane wejściowe:

bieżący stan niezatrzymany,
symbol w bieżącej komórce taśmy,

i generuje trzy wyjścia:

symbol do nadpisania nad symbolem w bieżącej komórce taśmy (może to być ten sam symbol, co symbol nadpisany),
kierunek ruchu (w lewo lub w prawo; to znaczy przesunięcie do komórki z taśmą o jedno miejsce w lewo lub w prawo od bieżącej komórki) oraz
stan do przejścia (który może być stanem zatrzymania).

Istnieją zatem (4 n + 4) ^{2 n} n -stanowe maszyny Turinga spełniające tę definicję, ponieważ ogólna postać formuły to ( symbole × kierunki × ( stany + 1)) ^{( symbole × stany )} .

Funkcję przejścia można postrzegać jako skończoną tablicę 5-krotek, z których każda ma postać

(aktualny stan, bieżący symbol, symbol do zapisania, kierunek przesunięcia, następny stan).

„Uruchomienie” maszyny polega na uruchomieniu w stanie początkowym, przy czym bieżącą komórką taśmy jest dowolna komórka pustej (wszystko-0) taśmy, a następnie iteracja funkcji przejścia, aż do przejścia w stan Halt (jeśli w ogóle). Jeśli i tylko wtedy, gdy maszyna w końcu się zatrzyma, to liczba jedynek pozostałych na taśmie nazywana jest wynikiem maszyny .

Gra zajęty bóbr w stanie n (BB- n ) polega na znalezieniu takiej maszyny Turinga w stanie n , która ma jak największy wynik — największą liczbę jedynek na taśmie po zatrzymaniu. Maszyna, która osiąga najwyższy możliwy wynik spośród wszystkich w stanie n , jest nazywana zajętym bobrem w stanie n , a maszyna, której wynik jest tylko najwyższym dotychczas osiągniętym (być może nie największym możliwym), nazywana jest mistrzem stanu n maszyna.

Radó wymagał, aby każdej maszynie zgłoszonej do konkursu towarzyszyło oświadczenie o dokładnej liczbie kroków potrzebnych do osiągnięcia stanu zatrzymania, co umożliwiło weryfikację wyniku każdego zgłoszenia (w zasadzie) poprzez uruchomienie maszyny dla podanej liczby kroków. (Gdyby wpisy miały składać się tylko z opisów maszyn, to problem weryfikacji każdego potencjalnego wpisu jest nierozstrzygalny, ponieważ jest równoważny dobrze znanemu problemowi zatrzymania — nie byłoby skutecznego sposobu decydowania, czy dowolna maszyna ostatecznie się zatrzyma.)

Powiązane funkcje

Zajęta funkcja bobra Σ

Funkcja zapracowanego bobra określa ilościowo maksymalny wynik, jaki może osiągnąć zapracowany bóbr w danej mierze. To jest funkcja nieobliczalna . Można również wykazać, że zajęta funkcja bobra rośnie asymptotycznie szybciej niż jakakolwiek funkcja obliczalna.

Zajęta funkcja bobra $,$ Σ ( n ) maksymalnym osiągalnym wynikiem (maksymalna liczba na taśmie) wśród wszystkich zatrzymanych 2-symbolowych n -stanowych maszyn Turinga opisanego powyżej typu, uruchamianych na pustej taśmie.

Jest oczywiste, że Σ jest dobrze zdefiniowaną funkcją: dla każdego n istnieje co najwyżej skończenie wiele n -stanowych maszyn Turinga, jak powyżej, aż do izomorfizmu, stąd co najwyżej skończenie wiele możliwych czasów działania.

Ta nieskończona sekwencja Σ jest zajętą funkcją bobra , a każda n -stanowa dwusymbolowa maszyna Turinga M , dla której σ ( M ) = Σ( n ) (tj. która osiąga maksymalny wynik) jest nazywana zajętym bobrem . Zauważ, że dla każdego n istnieją co najmniej cztery zajęte bobry w stanie n (ponieważ dla dowolnego zajętego bobra w stanie n inny jest uzyskiwany przez zwykłą zmianę kierunku przesunięcia w przejściu zatrzymującym, inny przez przesunięcie wszystkich zmian kierunku w kierunku przeciwnym , a finał poprzez zmianę kierunku zatrzymania zajętego bobra, który zamienił wszystkie miejsca).

Nieobliczalność

Artykuł Radó z 1962 roku udowodnił, że jeśli $jest$ dowolną obliczalną funkcją to Σ ( n ) > n dla wszystkich wystarczająco n , a zatem Σ nie jest funkcją obliczalną.

Co więcej, oznacza to, że za pomocą ogólnego algorytmu nie można rozstrzygnąć , czy dowolna maszyna Turinga jest pracowitym bobrem. (Taki algorytm nie może istnieć, ponieważ jego istnienie pozwoliłoby obliczyć Σ, co jest udowodnioną niemożliwością. W szczególności taki algorytm mógłby zostać użyty do skonstruowania innego algorytmu, który obliczałby Σ w następujący sposób: dla dowolnego danego n , każdy z skończenie wiele maszyn Turinga z dwoma symbolami w stanie n byłoby testowanych do momentu znalezienia zajętego bobra w stanie n ; ta zajęta maszyna bobra byłaby następnie symulowana w celu określenia jej wyniku, który z definicji wynosi Σ( n ).)

Mimo że Σ( n ) jest funkcją nieobliczalną, istnieją pewne małe n , dla których można uzyskać jej wartości i udowodnić, że są one poprawne. Nie jest trudno pokazać, że Σ(0) = 0, Σ(1) = 1, Σ(2) = 4, az coraz większymi trudnościami można wykazać, że Σ(3) = 6 i Σ(4) = 13 (sekwencja A028444 w OEIS ). Σ( n ) nie zostało jeszcze określone dla żadnego przypadku n > 4, chociaż ustalono dolne granice (patrz sekcja Znane wartości poniżej).

W 2016 roku Adam Yedidia i Scott Aaronson uzyskali pierwszą (wyraźną) górną granicę minimum n , dla którego Σ( n ) jest nie do udowodnienia w ZFC . Aby to zrobić, skonstruowali maszynę Turinga o 7910 stanach, której zachowania nie można udowodnić w oparciu o zwykłe aksjomaty teorii mnogości ( teoria mnogości Zermelo – Fraenkla z aksjomatem wyboru ), przy rozsądnych hipotezach spójności (stacjonarna właściwość Ramseya). Zostało to później zredukowane do 1919 stanów, z wyeliminowaną zależnością od stacjonarnej własności Ramseya, a później do 748 stanów.

Złożoność i niedowodliwość Σ

Wariant złożoności Kołmogorowa definiuje się następująco [por. Boolos, Burgess & Jeffrey, 2007]: Złożoność liczby n to najmniejsza liczba stanów potrzebnych dla maszyny Turinga klasy BB, która zatrzymuje się na pojedynczym bloku n kolejnych jedynek na początkowo pustej taśmie. Odpowiedni wariant twierdzenia Chaitina o niezupełności stwierdza, że w kontekście danego systemu aksjomatycznego dla liczb naturalnych , istnieje taka liczba k , że nie można udowodnić, że żadna konkretna liczba ma złożoność większą niż k , a zatem żadna konkretna górna granica można udowodnić dla Σ( k ) (to drugie jest spowodowane tym, że „złożoność n jest większa niż k ” zostałoby udowodnione, gdyby udowodniono „ n > Σ( k )”). Jak wspomniano w cytowanym odnośniku, dla dowolnego systemu aksjomatycznego „zwykłej matematyki” najmniejsza wartość k , dla której jest to prawdziwe, jest znacznie mniejsza niż 10↑↑10 ; w konsekwencji w kontekście zwykłej matematyki nie można udowodnić ani wartości, ani żadnej górnej granicy Σ (10 ↑↑ 10). ( Pierwsze twierdzenie Gödla o niezupełności ilustruje ten wynik: w systemie aksjomatycznym zwykłej matematyki istnieje zdanie prawdziwe, ale niedowodliwe w postaci „Σ(10 ↑↑ 10) = n” i istnieje nieskończenie wiele prawdziwych- ale-niedowolne zdania postaci "Σ(10 ↑↑ 10) < n ".)

Funkcja maksymalnych przesunięć S

Oprócz funkcji Σ, Radó [1962] wprowadził inną ekstremalną funkcję dla maszyn Turinga, funkcję maksymalnego przesunięcia , S , zdefiniowaną następująco:

$s (M)$ = liczba przesunięć, jakie M wykonuje przed zatrzymaniem, dla dowolnego $M \in E n$ ,
S ( n ) = maks. { s ( M ) | M ∈ E _n } = największa liczba przesunięć wykonanych przez dowolną zatrzymaną maszynę Turinga o 2-symbolach stanu n .

Ponieważ te maszyny Turinga muszą mieć przesunięcie w każdym przejściu lub „kroku” (w tym każdym przejściu do stanu zatrzymania), funkcja maksymalnych przesunięć jest jednocześnie funkcją maksymalnych kroków.

Radó wykazał, że S jest nieobliczalny z tego samego powodu, dla którego Σ jest nieobliczalny — rośnie szybciej niż jakakolwiek obliczalna funkcja. Udowodnił to po prostu zauważając, że dla każdego n , S ( n ) ≥ Σ( n ). Każda zmiana może zapisać na taśmie 0 lub 1, podczas gdy Σ liczy podzbiór zmian, które zapisały 1, a mianowicie te, które nie zostały nadpisane do czasu zatrzymania maszyny Turinga; w konsekwencji S rośnie co najmniej tak szybko jak Σ, co już zostało udowodnione, że rośnie szybciej niż jakakolwiek obliczalna funkcja.

Computer Studies of Turing Machine Problems ] wykorzystali następujący związek między Σ i S , aby udowodnić, że Σ(3) = 6: Dla danego n , jeśli S ( n ) jest znane, to wszystkie stany n Maszyny Turinga można (w zasadzie) uruchomić do S ( n ) kroków, w którym to momencie każda maszyna, która jeszcze się nie zatrzymała, nigdy się nie zatrzyma. W tym momencie, obserwując, które maszyny zatrzymały się z największą liczbą jedynek na taśmie (tj. pracowite bobry), uzyskuje się z ich taśm wartość Σ( n ). Podejście zastosowane przez Lin i Radó w przypadku n = 3 polegało na przypuszczeniu, że S (3) = 21, a następnie na symulacji wszystkich zasadniczo różnych maszyn trójstanowych dla maksymalnie 21 kroków. Analizując zachowanie maszyn, które nie zatrzymały się w ciągu 21 kroków, udało im się wykazać, że żadna z tych maszyn nigdy się nie zatrzyma, potwierdzając w ten sposób przypuszczenie, że S (3) = 21 i określając, że Σ (3) = 6 przez właśnie opisana procedura.

Nierówności odnoszące się do Σ i S obejmują następujące (z [Ben-Amram, et al., 1996]), które są ważne dla wszystkich $n \geq 1$ :

{\ Displaystyle {\ rozpocząć {wyrównane} S (n) i \ geq \ Sigma (n) \\ S (n) i \ równoważnik (2n-1) \ Sigma (3n + 3) \\ S (n) i < \Sigma (3n+6);\end{wyrównane}}}

oraz asymptotycznie ulepszoną granicę (z [Ben-Amram, Petersen, 2002]): istnieje stała c , taka, że dla wszystkich $n \geq 2$ ,

{\ Displaystyle S (n) \ równoważnik \ Sigma \ lewo (n + \ lewo \ lceil {\ Frac {8n} {\ log _ {2} n}} \ prawo \ rceil + c \ prawo).}

$)}$ $\ Displaystyle$ wydaje się być zbliżony do kwadratu , aw rzeczywistości wiele maszyn daje $)}$ ${\ Displaystyle S (n$ mniej niż ${\ Displaystyle \ Sigma ^ {2} (n)}$ .

Znane wartości dla Σ i S

Od 2016 roku wartości funkcji dla Σ ( n ) i S ( n ) są dokładnie znane tylko dla n <5.

Obecny (od 2018 r.) 5-stanowy mistrz ruchliwych bobrów produkuje 4098 1s, używając 47 176 870 kroków (odkrytych przez Heinera Marxena i Jürgena Buntrocka w 1989 r.), Ale pozostaje 18 lub 19 (prawdopodobnie poniżej 10, patrz poniżej) maszyny z nieregularne zachowanie, o którym uważa się, że nigdy się nie zatrzyma, ale którego nie udowodniono, że trwa w nieskończoność. Skelet wymienia 42 lub 43 niesprawdzone maszyny, ale 24 są już sprawdzone. Pozostałe maszyny zostały zasymulowane do 81,8 miliarda kroków, ale żadna nie została zatrzymana. Daniel Briggs udowodnił również niektóre maszyny. Inne źródło mówi, że 98 maszyn pozostaje niesprawdzonych. Jest analiza wstrzymań. Jest więc prawdopodobne, że Σ (5) = 4098 i S (5) = 47176870, ale pozostaje to nieudowodnione i nie wiadomo, czy pozostały jakieś blokady (od 2018 r.). W tej chwili rekordzista z 6 stanów produkuje ponad 3,514 7495 × 10 ^{18 267} 1s (dokładnie (25×4 ³⁰³⁴¹ +23)/9), wykorzystując ponad 7,412 × 10 ^{36 534} kroków (znalezionych przez Pavela Kropitza w 2010 r.). Jak wspomniano powyżej, są to 2-symbolowe maszyny Turinga.

Proste rozszerzenie maszyny 6-stanowej prowadzi do maszyny 7-stanowej, która zapisze na taśmie więcej niż 10 ^{10 ^{10 ^{10 ^{18 705 353 1s, ale bez wątpienia istnieją znacznie bardziej obciążone maszyny 7-stanowe.}}}} Jednak inni zapracowani łowcy bobrów mają różne zestawy maszyn.

Milton Green w swoim artykule z 1964 r. „A Lower Bound on Rado's Sigma Function for Binary Turing Machines” skonstruował zestaw maszyn Turinga wykazujący, że

{\ Displaystyle \ Sigma (2k)> 3 \ uparrow ^ {k-2} 3> A ( k-2,k-2)\qquad {\mbox{dla}}k\geq 2,}

gdzie ↑ to notacja Knutha ze strzałką w górę , a A to funkcja Ackermanna .

Zatem

{\ Displaystyle \ Sigma (10)> 3 \ góra \ góra \ góra 3 = 3 \ góra \ góra 3 ^ {3 ^ {3}} = 3 ^ {3 ^ {3 ^ {. ^ {. ^ {. ^{3}}}}}}}

(z 3 ^{3 ³} = 7 625 597 484 987 wyrazów w wieży wykładniczej) oraz

{\ Displaystyle \ Sigma (12)> 3 \ uparrow \ uparrow \ uparrow \ uparrow 3 = g_ {1},}

gdzie liczba g ₁ jest ogromną wartością początkową w ciągu definiującym liczbę Grahama .

W 1964 roku Milton Green opracował dolną granicę funkcji Busy Beaver, która została opublikowana w materiałach z sympozjum IEEE w 1964 roku na temat teorii obwodów przełączających i projektowania logicznego. Heiner Marxen i Jürgen Buntrock opisali to jako „nietrywialną (nie prymitywną rekurencyjną) dolną granicę”. Tę dolną granicę można obliczyć, ale jest ona zbyt złożona, aby można ją było podać jako pojedyncze wyrażenie wyrażone w postaci n. Gdy n=8 metoda daje Σ(8) ≥ 3 × (7 × 3 ⁹² - 1) / 2 ≈ 8,248×10 ⁴⁴ .

Z aktualnych dolnych granic można wywnioskować, że:

{\ Displaystyle \ Sigma (2k + 1)> 3 \ uparrow ^ {k-2} 31>A(k-2,k-2)\qquad {\mbox{dla }}k\geq 2,}

W przeciwieństwie do tego, najlepsza aktualna (stan na 2018 r.) Dolna granica Σ(6) wynosi 10 ^{18 267} , czyli jest większa niż dolna granica określona wzorem Greena, 3 ³ = 27 (która jest niewielka w porównaniu). W rzeczywistości jest znacznie większy niż dolna granica: 3 ↑↑ 3 = 3 ^{3 ³} = 7 625 597 484 987 , co jest pierwszą dolną granicą Greena dla Σ(8), a także znacznie większą niż druga dolna granica: 3 ×(7×3 ⁹² −1)/2.

Σ(7) jest w ten sam sposób znacznie, znacznie większe niż obecna wspólna dolna granica 3 ³¹ (prawie 618 bilionów), więc druga dolna granica jest również bardzo, bardzo słaba.

Dowód na nieobliczalność S ( n ) i Σ ( n )

₀₀₀₀₀₀ Załóżmy, że S ( n ) jest funkcją obliczalną i niech EvalS oznacza TM, oceniającą S ( n ). Biorąc pod uwagę taśmę z n 1s, wytworzy S ( n ) 1s na taśmie, a następnie zatrzyma się. Niech Clean oznacza maszynę Turinga czyszczącą sekwencję jedynek zapisaną początkowo na taśmie. Niech Double oznacza funkcję oceniającą maszynę Turinga n + n . Biorąc pod uwagę taśmę z n 1s, wytworzy 2 n 1s na taśmie, a następnie zatrzyma się. Stwórzmy kompozycję Double | Oceny | Wyczyść i niech n będzie liczbą stanów tej maszyny. Niech Create_n ₀ oznacza maszynę Turinga tworzącą n jedynek na początkowo pustej taśmie. Maszyna ta może być skonstruowana w trywialny sposób tak, aby miała n stanów (stan i zapisuje 1, porusza głową w prawo i przełącza się do stanu i + 1, z wyjątkiem stanu n , który się zatrzymuje). Niech N oznacza sumę n + n .

₀ Niech BadS oznacza kompozycję Create_n ₀ | Podwójne | Oceny | czysty . Zauważ, że ta maszyna ma N stanów. Rozpoczynając od początkowo pustej taśmy, najpierw tworzy sekwencję n 1, a następnie podwaja ją, tworząc sekwencję N 1. Następnie BadS wyprodukuje S ( N ) 1 na taśmie iw końcu usunie wszystkie 1, a następnie zatrzyma się. Ale faza czyszczenia będzie trwała co najmniej S ( N ) kroków, więc czas działania BadS jest ściśle większy niż S ( N ), co jest sprzeczne z definicją funkcji S ( n ).

Nieobliczalność Σ( n ) można udowodnić w podobny sposób. W powyższym dowodzie należy zamienić maszynę EvalS na EvalΣ i Clean na Increment — prostą TM, szukanie pierwszego 0 na taśmie i zastępowanie go 1.

Nieobliczalność S ( n ) można również ustalić przez odniesienie do problemu zatrzymania pustej taśmy. Problem zatrzymywania pustej taśmy to problem decydowania dla dowolnej maszyny Turinga, czy zatrzyma się ona po uruchomieniu na pustej taśmie. Problem zatrzymania pustej taśmy jest równoważny standardowemu problemowi zatrzymania , więc jest również nieobliczalny. Gdyby S ( n ) było obliczalne, moglibyśmy rozwiązać problem zatrzymywania pustej taśmy po prostu uruchamiając dowolną maszynę Turinga z n stanami dla S ( n ) kroków; jeśli nadal się nie zatrzymał, nigdy się nie zatrzyma. Tak więc, ponieważ problem zatrzymania pustej taśmy nie jest obliczalny, wynika z tego, że S ( n ) również musi być nieobliczalny.

Uogólnienia

Dla każdego modelu obliczeniowego istnieją proste analogie pracowitego bobra. Na przykład uogólnienie na maszyny Turinga z n stanami i m symbolami definiuje następujące uogólnione zajęte funkcje bobra :

Σ( n , m ): największa liczba zer niezerowych, które można wydrukować przez maszynę o stanie n , symbolu m , uruchomioną na początkowo pustej taśmie przed zatrzymaniem, oraz
S ( n , m ): największa liczba kroków wykonanych przez n -stanową maszynę o symbolu m uruchomioną na początkowo pustej taśmie przed zatrzymaniem.

Na przykład, najdłużej działająca maszyna z trzema stanami i trzema symbolami, znaleziona do tej pory, wykonuje 119 112 334 170 342 540 kroków przed zatrzymaniem. ^{[ Potrzebne źródło ]} Najdłużej działająca 6-stanowa maszyna z 2 symbolami, która ma dodatkową właściwość odwracania wartości na taśmie w każdym kroku, wytwarza 6147 1s po 47 339 970 krokach. ^{[ potrzebne źródło ]} Tak więc dla klasy Odwrotnej Maszyny Turinga (RTM), SR _RTM (6) ≥ 47 339 970 i Σ _RTM (6) ≥ 6147 .

Możliwe jest dalsze uogólnienie funkcji ruchliwego bobra poprzez rozszerzenie na więcej niż jeden wymiar.

Podobnie moglibyśmy zdefiniować analogię do funkcji Σ dla maszyn rejestrowych jako największą liczbę, która może być obecna w dowolnym rejestrze podczas zatrzymania, dla danej liczby instrukcji.

Dokładne wartości i dolne granice

Poniższa tabela zawiera dokładne wartości i niektóre znane dolne granice dla S ( n , m ) i Σ( n , m ) dla uogólnionych problemów ruchliwego bobra. Uwaga: wpisy wymienione jako „?” są ograniczone od dołu przez maksimum wszystkich wpisów z lewej i z góry. Te maszyny albo nie zostały zbadane, albo zostały później prześcignięte przez mniejszą maszynę.

Maszyny Turinga, które osiągają te wartości, są dostępne na stronie internetowej Pascala Michela . Ta strona internetowa zawiera również pewne analizy maszyn Turinga i odniesienia do dowodów dokładnych wartości.

N M	2 stany	3 stany	4 stany	5-stan	6-stan
Wartości S( n , m )
2-symbol	6	21	107	47 176 870 ?	> 10 ${\ Displaystyle \ górna \ górna część}$ 15
3-symbol	38	≥ 119 112 334 170 342 540	> 1,0 × 10 ^{14 072}	?	?
4-symbol	≥ 3 932 964	> 5,2 × 10 ^{13 036}	?	?	?
5-symbol	> 1,9 × 10 ⁷⁰⁴	?	?	?	?
6-symbol	> 2,4 × 10 ⁹⁸⁶⁶	?	?	?	?
Wartości Σ( n , m )
N M	2 stany	3 stany	4 stany	5-stan	6-stan
2-symbol	4	6	13	4098 ?	> 10 ${\ Displaystyle \ górna \ górna część}$ 15
3-symbol	9	≥ 374 676 383	> 1,3 × 10 ⁷⁰³⁶	?	?
4-symbol	≥ 2050	> 3,7 × 10 ⁶⁵¹⁸	?	?	?
5-symbol	> 1,7 × 10 ³⁵²	?	?	?	?
6-symbol	> 1,9 × 10 ⁴⁹³³	?	?	?	?

Niedeterministyczne maszyny Turinga

Maksymalne czasy i stany zatrzymania z przypadku p , 2-stanowe, 2-kolorowe NDTM
P	kroki	stany
1	2	2
2	4	4
3	6	7
4	7	11
5	8	15
6	7	18
7	6	18

Problem można rozszerzyć na niedeterministyczne maszyny Turinga , szukając systemu z największą liczbą stanów we wszystkich gałęziach lub gałęzi z najdłuższą liczbą kroków. Pytanie, czy dany NDTM się zatrzyma, jest nadal nieredukowalne obliczeniowo, a obliczenia wymagane do znalezienia zajętego bobra NDTM są znacznie większe niż w przypadku deterministycznym, ponieważ należy wziąć pod uwagę wiele gałęzi. W przypadku systemu dwustanowego i dwukolorowego z p przypadkami lub regułami tabela po prawej podaje maksymalną liczbę kroków przed zatrzymaniem i maksymalną liczbę unikalnych stanów utworzonych przez NDTM.

Aplikacje

Oprócz dość trudnej gry matematycznej , zajęte funkcje bobra oferują zupełnie nowe podejście do rozwiązywania czysto matematycznych problemów. Wiele otwartych problemów matematycznych można by teoretycznie, ale nie w praktyce, rozwiązać w systematyczny sposób, biorąc pod uwagę wartość S ( n ) dla dostatecznie dużego n .

Rozważ dowolne przypuszczenie , które można obalić za pomocą kontrprzykładu spośród policzalnej liczby przypadków (np. przypuszczenie Goldbacha ). Napisz program komputerowy, który sekwencyjnie sprawdza tę hipotezę pod kątem rosnących wartości. W przypadku hipotezy Goldbacha rozważylibyśmy kolejno każdą liczbę parzystą ≥ 4 i sprawdzilibyśmy, czy jest ona sumą dwóch liczb pierwszych. Załóżmy, że ten program jest symulowany na n -stanowej maszynie Turinga. Jeśli znajdzie kontrprzykład (liczbę parzystą ≥ 4, która nie jest sumą dwóch liczb pierwszych w naszym przykładzie), zatrzymuje się i wskazuje to. Jeśli jednak przypuszczenie jest prawdziwe, nasz program nigdy się nie zatrzyma. (Ten program zatrzymuje się tylko wtedy, gdy znajdzie kontrprzykład).

Teraz ten program jest symulowany przez n -stanową maszynę Turinga, więc jeśli znamy S ( n ), możemy zdecydować (w skończonym czasie), czy kiedykolwiek się zatrzyma, po prostu uruchamiając maszynę w tylu krokach. A jeśli po S ( n ) maszyna się nie zatrzyma, wiemy, że nigdy się nie zatrzyma, a zatem nie ma kontrprzykładów dla danego przypuszczenia (tj. nie ma liczb parzystych, które nie są sumą dwóch liczb pierwszych). To by potwierdzało prawdziwość przypuszczenia.

W ten sposób określone wartości (lub górne granice) dla S ( n ) mogą być wykorzystywane do systematycznego rozwiązywania wielu otwartych problemów matematycznych (w teorii). Jednak obecne wyniki dotyczące problemu ruchliwych bobrów sugerują, że nie będzie to praktyczne z dwóch powodów:

Niezwykle trudno jest udowodnić wartości funkcji zajętego bobra (i funkcji maksymalnego przesunięcia). Udowodniono to tylko dla bardzo małych maszyn z mniej niż pięcioma stanami, podczas gdy przypuszczalnie potrzeba co najmniej 20-50 stanów ^{[ potrzebne źródło ]} , aby stworzyć użyteczną maszynę. Co więcej, każda znana dokładna wartość S ( n ) została udowodniona poprzez wyliczenie każdej n -stanowej maszyny Turinga i udowodnienie, czy każda z nich się zatrzymuje. Trzeba by obliczyć S ( n ) jakąś mniej bezpośrednią metodą, żeby była użyteczna.
Ale nawet gdyby udało się znaleźć lepszy sposób obliczenia S ( n ), wartości zajętej funkcji bobra (i funkcji maksymalnego przesunięcia) stają się bardzo duże, bardzo szybko. S (6) > 10 ^{36 534} wymaga już specjalnego przyspieszenia opartego na wzorach, aby móc symulować do końca. Podobnie wiemy, że S (10) > Σ(10) > 3 ↑↑↑ 3 jest liczbą gigantyczną, a S (17) > Σ(17) > G, gdzie G jest liczbą Grahama - liczbą ogromną. Tak więc, nawet gdybyśmy znali, powiedzmy, S (30), jest całkowicie nierozsądne uruchamianie jakiejkolwiek maszyny z taką liczbą kroków. W znanej części wszechświata nie ma wystarczającej mocy obliczeniowej, aby bezpośrednio wykonać nawet S (6).

Godne uwagi przypadki

Skonstruowano 748-stanową binarną maszynę Turinga, która zatrzymuje się, jeśli ZFC jest niespójne. Skonstruowano 744-stanową maszynę Turinga, która zatrzymuje się, jeśli hipoteza Riemanna jest fałszywa. Skonstruowano 43-stanową maszynę Turinga, która zatrzymuje się, jeśli hipoteza Goldbacha jest fałszywa, a 27-stanowa maszyna dla tego przypuszczenia została zaproponowana, ale jeszcze nie zweryfikowana.

Skonstruowano 15-stanową maszynę Turinga, która zatrzymuje się, jeśli następujące przypuszczenie sformułowane przez Paula Erdősa w 1979 roku jest fałszywe: dla każdego n > 8 jest co najmniej jedna cyfra 2 w reprezentacji 2 ^{n o podstawie 3} .

Przykłady

Pokazuje pierwsze 100 000 kroków czasowych aktualnie najlepszego zajętego bobra w 5 stanach. Pomarańczowy to „1”, biały to „0” (obraz skompresowany w pionie).

Są to tablice reguł dla maszyn Turinga, które generują Σ(1) i S (1), Σ(2) i S (2), Σ(3) (ale nie S (3)), Σ(4) i S (4) oraz najlepiej znana dolna granica dla Σ(5) i S (5) oraz Σ(6) i S (6). W przypadku innych wizualizacji

W tabelach kolumny przedstawiają aktualny stan, a wiersze aktualny symbol odczytany z taśmy. Każdy wpis w tabeli to ciąg trzech znaków wskazujących symbol do zapisania na taśmie, kierunek ruchu i nowy stan (w tej kolejności). Stan zatrzymania jest pokazany jako H .

Każda maszyna rozpoczyna się w stanie A z nieskończoną taśmą zawierającą same zera. Zatem symbolem początkowym odczytanym z taśmy jest 0.

Klawisz wyniku: (rozpoczyna się w pozycji podkreślonej , zatrzymuje się w pozycji podkreślonej )

1-stan, 2-symbol zajęty bóbr
	1R
0	H _
1	(nieużywany)

0 Wynik: 0 0 1 0 (1 krok, łącznie jeden „1”)

2-stanowy, 2-symbolowy zajęty bóbr ^{[ potrzebne źródło ]}
	A	B
0	1R B	1L A
1	1L B	1R H

Wynik: 0 0 1 1 1 1 0 0 (6 kroków, łącznie cztery „1”)

Animacja 3-stanowego, 2-symbolowego ruchliwego bobra

3-stanowy, 2-symbolowy zajęty bóbr
	A	B	C
0	1R B	0R C	1L C
1	1R H	1R B	1L A

Wynik: 0 0 1 1 1 1 1 1 0 0 (14 kroków, łącznie sześć „1”).

W przeciwieństwie do poprzednich maszyn, ta jest pracowitym bobrem tylko dla Σ, ale nie dla S . ( S (3) = 21.)

Animacja 4-stanowego, 2-symbolowego ruchliwego bobra

4-stanowy, 2-symbolowy ruchliwy bóbr
	A	B	C	D
0	1R B	1L A	1R H	1R D
1	1L B	0L C	1L D	0R A

0 Wynik: 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 (107 kroków, łącznie trzynaście „1”)

obecny 5-stanowy, 2-symbolowy najlepszy pretendent (prawdopodobnie zapracowany bóbr)
	A	B	C	D	mi
0	1R B	1R C	1R D	1L A	1R H
1	1L C	1R B	0L E	1L D	0L A

Wynik: 4098 „1” z 8191 „0” przeplatanych 47 176 870 krokami.

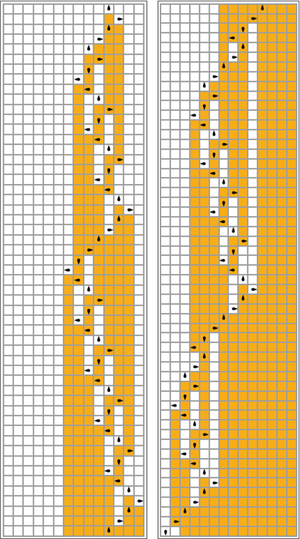
Zauważ na obrazku po prawej, jak to rozwiązanie jest jakościowo podobne do ewolucji niektórych automatów komórkowych .

obecny 6-stanowy, 2-symbolowy najlepszy pretendent ^{[ potrzebne źródło ]}
	A	B	C	D	mi	F
0	1R B	1R C	1L C	0L E	1L F	0R C
1	0L D	0R F	1L A	1R H	0R B	0R E

0 Wynik: 1 1 1 1 ... 1 1 1 („10”, po którym następuje więcej niż 10↑↑15 ciągłych „1” w więcej niż 10↑↑15 krokach, gdzie 10↑↑15=10 ^{10 ^{. ^{. ¹⁰}}} , wieża wykładnicza 15 dziesiątek).

Wizualizacje

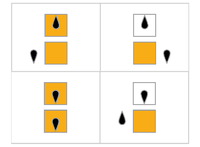
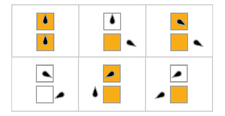
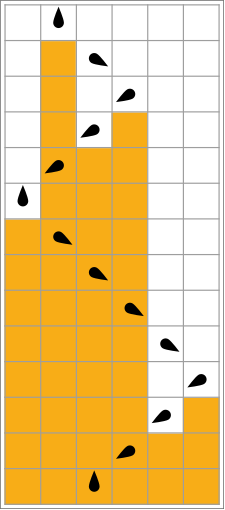
W poniższej tabeli reguły dla każdego ruchliwego bobra (maksymalizacja Σ) są przedstawione wizualnie, z pomarańczowymi kwadratami odpowiadającymi „1” na taśmie i białym odpowiadającym „0”. Położenie głowy wskazuje czarny jajowaty kształt, przy czym orientacja głowy reprezentuje stan. Poszczególne taśmy ułożone są poziomo, z upływem czasu od góry do dołu. Stan zatrzymania jest reprezentowany przez regułę, która odwzorowuje jeden stan na siebie (głowa się nie porusza).

Ewolucja zapracowanych bobrów z 1-4 stanami

Zasady dla ruchliwego bobra w 1 stanie.

Zasady dla ruchliwego bobra w 2 stanach.

Zasady dla ruchliwego bobra w 3 stanach.

Zasady dla ruchliwego bobra w 4 stanach.

Ewolucja ruchliwego bobra w stanie 1 do zatrzymania. Stan początkowy powoduje zatrzymanie, z pojedynczym „1” zapisywanym przed zakończeniem.

Ewolucja dwustanowego ruchliwego bobra aż do zatrzymania.

Ewolucja 3-stanowego ruchliwego bobra aż do zatrzymania.

Ewolucja 4-stanowego ruchliwego bobra aż do zatrzymania. Dolna linia lewego obrazu zawija się do górnej linii prawego obrazu. Ostatni krok zapisuje „1” przed zatrzymaniem (nie pokazano).

Zobacz też

Notatki

^ ^a ^b Radó, Tibor (maj 1962). „O funkcjach nieobliczalnych” (PDF) . Dziennik techniczny systemu Bell . 41 (3): 877–884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
Bibliografia _
^ Adam Yedidia i Scott Aaronson (maj 2016). Stosunkowo mała maszyna Turinga, której zachowanie jest niezależne od teorii mnogości (raport techniczny). MIT. ar Xiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .
Bibliografia _ „Ta maszyna Turinga powinna działać wiecznie, chyba że matematyka się myli” . Źródło 2016-09-25 .
^ ^a ^b Wersja z 3 maja zawierała 7918 stanów: „8000-ty numer Busy Beaver wymyka się teorii mnogości ZF” . Blog zoptymalizowany pod kątem Shtetl . 2016-05-03 . Źródło 2016-09-25 .
^ ^a ^b ^c „Trzy ogłoszenia” . Blog zoptymalizowany pod kątem Shtetl . 2016-05-03 . Źródło 2018-04-27 .
Bibliografia _ _ GitHub . 2019-02-13.
^ „Zapracowana granica bobrów” (PDF) .
^ „Strona szkieletu dotycząca problemu zajętego bobra” . szkielet.ludost.net .
^ Turing: Projekt zakończenia pracowitego bobra z 5
^ „Problem zapracowanego bobra: NOWY ATAK MILLENNIUM” .
^ „Odwrotna maszyna Turinga” . szkielet.ludost.net . Źródło 2022-02-10 .
^ ^ab ⁽ Wolfram, Stephen 4 lutego 2021). „Wielokierunkowe maszyny Turinga” . www.wolframphysics.org .
Bibliografia _
^ Lloyd 2001. Zdolność obliczeniowa Wszechświata .
^ ^abc ^{Pavlus ,}^John (10 grudnia 2020). „Jak najwolniejsze programy komputerowe oświetlają podstawowe ograniczenia matematyki” . Magazyn Quanta . Źródło 2020-12-11 .
^ Tristan Stérin i Damien Woods (lipiec 2021). O twardości znając wartości ruchliwego bobra BB(15) i BB(5,4) (raport techniczny). Uniwersytet Maynooth. arXiv : 2107.12475 .
^ Erdos, Paweł (1979). „Niektóre niekonwencjonalne problemy w teorii liczb” . Matematyka Mag. 52 (2): 67–70. doi : 10.1080/0025570X.1979.11976756 . JSTOR 2689842 .
Bibliografia _ Komputerowe studia problemów maszyny Turinga (praca doktorska). Uniwersytet Stanowy Ohio .
Bibliografia _ Rado, Tibor (kwiecień 1965). „Komputerowe badania problemów z maszyną Turinga”. Dziennik ACM . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .

Radó, Tibor (maj 1962). „O funkcjach nieobliczalnych” (PDF) . Dziennik techniczny systemu Bell . 41 (3): 877–884. doi : 10.1002/j.1538-7305.1962.tb00480.x .
To tutaj Radó po raz pierwszy zdefiniował problem ruchliwego bobra i udowodnił, że jest on nieobliczalny i rośnie szybciej niż jakakolwiek obliczalna funkcja.
Lin, Shen; Radó, Tibor (kwiecień 1965). „Komputerowe badania problemów z maszyną Turinga” . Dziennik ACM . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .
Wyniki tego artykułu pojawiły się już częściowo w rozprawie doktorskiej Lin z 1963 r., Pod kierunkiem Radó. Lin i Radó dowodzą, że Σ(3) = 6 i S (3) = 21, udowadniając, że wszystkie 3-stanowe 2-symbolowe maszyny Turinga, które nie zatrzymują się w ciągu 21 kroków, nigdy się nie zatrzymają. (Większość jest sprawdzana automatycznie przez program komputerowy, jednak 40 jest sprawdzanych przez człowieka).
Brady, Allen H. (kwiecień 1983). „Wyznaczanie wartości nieobliczalnej funkcji Rado Σ( k ) dla czterostanowych maszyn Turinga” . Matematyka obliczeń . 40 (162): 647–665. doi : 10.1090/S0025-5718-1983-0689479-6 . JSTOR 2007539 .
Brady udowadnia, że Σ(4) = 13 i S (4) = 107. Brady definiuje dwie nowe kategorie dla nie zatrzymujących się 3-stanowych 2-symbolowych Maszyn Turinga: Choinki i Liczniki. Używa programu komputerowego, aby udowodnić, że wszystkie oprócz 27 maszyn, które wykonują ponad 107 kroków, są wariantami choinek i liczników, co do których można udowodnić, że działają w nieskończoność. Ostatnie 27 maszyn (określanych jako wstrzymane) zostało udowodnione przez osobistą inspekcję samego Brady'ego, że się nie zatrzymują.
Macchlin, Rona; Stout, Quentin F. (czerwiec 1990). „Złożone zachowanie prostych maszyn” . Physica D: Zjawiska nieliniowe . 42 (1–3): 85–98. Bibcode : 1990PhyD...42...85M . doi : 10.1016/0167-2789(90)90068-Z . hdl : 2027.42/28528 .
Macchlin i Stout opisują problem ruchliwych bobrów i wiele technik używanych do znajdowania ruchliwych bobrów (które stosują do maszyn Turinga z 4-stanami i 2-symbolami, weryfikując w ten sposób dowód Brady'ego). Sugerują, jak oszacować wariant prawdopodobieństwa zatrzymania Chaitina (Ω).
Marksen, Heiner; Buntrock, Jürgen (luty 1990). „Atak na ruchliwego bobra 5” . Biuletyn EATCS . 40 : 247–251. Zarchiwizowane od oryginału w dniu 2006-10-09 . Źródło 2020-01-19 .
Marxen i Buntrock wykazują, że Σ(5) ≥ 4098 i S (5) ≥ 47 176 870 i szczegółowo opisują metodę, której użyli do znalezienia tych maszyn i udowodnienia, że wiele innych nigdy się nie zatrzyma.
Zielony, Milton W. (1964). Dolna granica funkcji Sigma Rado dla binarnych maszyn Turinga . 1964 Materiały z piątego dorocznego sympozjum na temat teorii obwodów przełączających i projektowania logicznego . s. 91–94. doi : 10.1109/SWCT.1964.3 .
Green rekurencyjnie konstruuje maszyny dla dowolnej liczby stanów i zapewnia funkcję rekurencyjną, która oblicza ich wynik (oblicza σ), zapewniając w ten sposób dolną granicę dla Σ. Wzrost tej funkcji jest porównywalny ze wzrostem funkcji Ackermanna .
Dewdney, Aleksander K. (1984). „Komputerowa pułapka na pracowitego bobra, najciężej pracująca maszyna Turinga”. Naukowy Amerykanin . 251 (2): 10–17.
Zajęte programy bobrów zostały opisane przez Alexandra Dewdneya w Scientific American , sierpień 1984, strony 19–23, także marzec 1985, s. 23 i kwietnia 1985 s. 30 .
Chaitin, Gregory J. (1987). „Obliczanie funkcji zajętego bobra” (PDF) . W okładce, TM; Gopinath, B. (red.). Otwarte problemy w komunikacji i obliczeniach . Skoczek. s. 108–112. ISBN 978-0-387-96621-2 .
Brady, Allen H. (1995). „Gra w pracowitego bobra i sens życia”. W Herken, Rolf (red.). Uniwersalna maszyna Turinga: przegląd pół wieku (wyd. 2). Wien, Nowy Jork: Springer-Verlag. s. 237–254. ISBN 978-3-211-82637-9 .
W którym Brady (sławny w 4 stanach) opisuje historię bestii i nazywa jej pościg „Grą zapracowanego bobra”. Opisuje inne gry (np. automaty komórkowe i Conway's Game of Life ). Szczególnie interesująca jest „Gra pracowitego bobra w dwóch wymiarach” (s. 247). Z 19 referencjami.
Booth, Taylor L. (1967). Teoria maszyn sekwencyjnych i automatów . Nowy Jork: Wiley. ISBN 978-0-471-08848-6 .
Por. rozdział 9, Maszyny Turinga. Trudna książka, przeznaczona dla inżynierów elektryków i specjalistów technicznych. Omawia rekurencję, częściową rekurencję w odniesieniu do Maszyn Turinga, problem zatrzymania. Wzmianka w Booth przypisuje rado zapracowanego bobra. Booth definiuje również problem ruchliwego bobra Rado w „problemach domowych” 3, 4, 5, 6 rozdziału 9, s. 396. Zadanie 3 polega na „pokazaniu, że problem ruchliwego bobra jest nierozwiązywalny… dla wszystkich wartości n”.
Ben-Amram, AM; Julstrom, BA; Zwick, U. (1996). „Uwaga na temat pracowitych bobrów i innych stworzeń” . Teoria systemów matematycznych . 29 (4): 375–386. CiteSeerX 10.1.1.75.1297 . doi : 10.1007/BF01192693 . S2CID 30937913 .
Granice między funkcjami Σ i S .
Ben-Amram, AM; Petersen, H. (2002). „Poprawione granice funkcji związanych z pracowitymi bobrami”. Teoria systemów komputerowych . 35 : 1–11. CiteSeerX 10.1.1.136.5997 . doi : 10.1007/s00224-001-1052-0 . S2CID 10429773 .
Ulepszone granice.
Lafitte, G.; Papazian, C. (czerwiec 2007). „Tkanina małych maszyn Turinga”. Obliczenia i logika w świecie rzeczywistym, Proceedings of the Third Conference on Computability in Europe . s. 219–227. CiteSeerX 10.1.1.104.3021 .
Ten artykuł zawiera pełną klasyfikację 2-stanowych, 3-symbolowych maszyn Turinga, a tym samym dowód na (2, 3) ruchliwego bobra: Σ (2, 3) = 9 i S (2, 3) = 38.
Boolos, George S.; Burgess, John P.; Jeffrey, Richard C. (2007). Obliczalność i logika (wyd. Piąte). Wydawnictwo Uniwersytetu Cambridge. ISBN 978-0-521-87752-7 .
Kropitz, Paweł (2010). Problem Busy Beaver (praca licencjacka) (po słowacku). Uniwersytecie Karola w Pradze.
Jest to opis pomysłów, algorytmów i ich implementacji, z opisem eksperymentów badających 5- i 6-stanową maszynę Turinga przez równoległe uruchomienie na 31 4-rdzeniowym komputerze i wreszcie najlepsze wyniki dla 6-stanowej TM.

Linki zewnętrzne

Strona Heinera Marxena , który wraz z Jürgenem Buntrockiem znalazł wspomniane wyżej zapisy dla 5 i 6-stanowej maszyny Turinga.
Historyczny przegląd wyników pracowitych bobrów Pascala Michela , który zawiera również najlepsze wyniki i pewną analizę.
Definicja klasy RTM - Reversal Turing Machines, prosta i mocna podklasa TM.
„ Problem zapracowanego bobra: atak nowego tysiąclecia ” ( archiwum ) w Rensselaer RAIR Lab. Ten wysiłek znalazł kilka nowych rekordów i ustalił kilka wartości dla poczwórnej formalizacji.
Archiwum strony Daniela Briggsa i forum do rozwiązywania problemu zajętego bobra z 5 stanami i 2 symbolami, na podstawie listy nieregularnych maszyn Skelet (Georgi Georgiev).
Ligocki, Shawn (2021-07-17). „Zachowanie pracowitych bobrów podobne do Collatza” . śligocki . Źródło 2022-07-12 .
Aaronson, Scott (1999), Kto potrafi wymienić największą liczbę?
Weisstein, Eric W. „Zajęty Bóbr” . MathWorld .
Busy Beaver Turing Machines - Computerphile , Youtube
Pascala Michela. Konkurs pracowitego bobra: przegląd historyczny . 70 stron. 2017. <hal-00396880v5>

[rado-1] Radó, Tibor (maj 1962). „O funkcjach nieobliczalnych” (PDF) . Dziennik techniczny systemu Bell . 41 (3): 877–884. doi : 10.1002/j.1538-7305.1962.tb00480.x .

[2] Bibliografia _

[3] Adam Yedidia i Scott Aaronson (maj 2016). Stosunkowo mała maszyna Turinga, której zachowanie jest niezależne od teorii mnogości (raport techniczny). MIT. ar Xiv : 1605.04343 . Bibcode : 2016arXiv160504343Y .

[4] Bibliografia _ „Ta maszyna Turinga powinna działać wiecznie, chyba że matematyka się myli” . Źródło 2016-09-25 .

[:0-5] Wersja z 3 maja zawierała 7918 stanów: „8000-ty numer Busy Beaver wymyka się teorii mnogości ZF” . Blog zoptymalizowany pod kątem Shtetl . 2016-05-03 . Źródło 2016-09-25 .

[Aaronson3-6] „Trzy ogłoszenia” . Blog zoptymalizowany pod kątem Shtetl . 2016-05-03 . Źródło 2018-04-27 .

[7] Bibliografia _ _ GitHub . 2019-02-13.

[8] „Zapracowana granica bobrów” (PDF) .

[9] „Strona szkieletu dotycząca problemu zajętego bobra” . szkielet.ludost.net .

[10] Turing: Projekt zakończenia pracowitego bobra z 5

[11] „Problem zapracowanego bobra: NOWY ATAK MILLENNIUM” .

[12] „Odwrotna maszyna Turinga” . szkielet.ludost.net . Źródło 2022-02-10 .

[NDTM-13] ⁽ Wolfram, Stephen 4 lutego 2021). „Wielokierunkowe maszyny Turinga” . www.wolframphysics.org .

[14] Bibliografia _

[15] Lloyd 2001. Zdolność obliczeniowa Wszechświata .

[:1-16] {Pavlus ,}^John (10 grudnia 2020). „Jak najwolniejsze programy komputerowe oświetlają podstawowe ograniczenia matematyki” . Magazyn Quanta . Źródło 2020-12-11 .

[17] Tristan Stérin i Damien Woods (lipiec 2021). O twardości znając wartości ruchliwego bobra BB(15) i BB(5,4) (raport techniczny). Uniwersytet Maynooth. arXiv : 2107.12475 .

[18] Erdos, Paweł (1979). „Niektóre niekonwencjonalne problemy w teorii liczb” . Matematyka Mag. 52 (2): 67–70. doi : 10.1080/0025570X.1979.11976756 . JSTOR 2689842 .

[19] Bibliografia _ Komputerowe studia problemów maszyny Turinga (praca doktorska). Uniwersytet Stanowy Ohio .

[20] Bibliografia _ Rado, Tibor (kwiecień 1965). „Komputerowe badania problemów z maszyną Turinga”. Dziennik ACM . 12 (2): 196–212. doi : 10.1145/321264.321270 . S2CID 17789208 .