Prawa obwodowe Kirchhoffa

Aby zapoznać się z innymi prawami nazwanymi na cześć Gustava Kirchhoffa, zobacz prawa Kirchhoffa .

Prawa obwodowe Kirchhoffa to dwie równości , które dotyczą różnicy prądu i potencjału (powszechnie znanej jako napięcie) w modelu elementów skupionych obwodów elektrycznych . Zostały one po raz pierwszy opisane w 1845 roku przez niemieckiego fizyka Gustava Kirchhoffa . To uogólniło pracę Georga Ohma i poprzedziło pracę Jamesa Clerka Maxwella . Szeroko stosowane w elektrotechnice , nazywane są również regułami Kirchhoffa lub po prostu Prawa Kirchhoffa . Prawa te mogą być stosowane w dziedzinie czasu i częstotliwości i stanowią podstawę analizy sieci .

Oba prawa Kirchhoffa można rozumieć jako następstwa równań Maxwella w zakresie niskich częstotliwości. Są dokładne dla obwodów prądu stałego oraz obwodów prądu przemiennego przy częstotliwościach, w których długości fal promieniowania elektromagnetycznego są bardzo duże w porównaniu z obwodami.

Obecne prawo Kirchhoffa

Prąd wpływający do dowolnego złącza jest równy prądowi opuszczającemu to złącze. ja ₂ + ja ₃ = ja ₁ + ja ₄

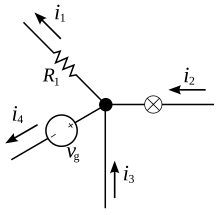
To prawo, zwane także pierwszym prawem Kirchhoffa lub regułą połączeń Kirchhoffa , stwierdza, że ​​dla dowolnego węzła (węzła) w obwodzie elektrycznym suma prądów wpływających do tego węzła jest równa sumie prądów wypływających z tego węzła; lub równoważnie:

Algebraiczna suma prądów w sieci przewodników spotykających się w jednym punkcie wynosi zero.

Pamiętając, że prąd jest wielkością ze znakiem (dodatnią lub ujemną) odzwierciedlającą kierunek do lub od węzła, zasadę tę można zwięźle sformułować jako:

$${\ Displaystyle \ suma _ {k = 1} ^ {n} {I} _ {k} = 0}$$

gdzie n to całkowita liczba gałęzi z prądami płynącymi do lub od węzła.

Prawa obwodowe Kirchhoffa zostały pierwotnie uzyskane z wyników eksperymentalnych. Jednak obecne prawo można postrzegać jako rozszerzenie zasady zachowania ładunku , ponieważ ładunek jest iloczynem prądu i czasu, w którym płynął prąd. Jeśli opłata netto w regionie jest stała, obecne prawo będzie obowiązywało na granicach regionu. Oznacza to, że obecne prawo opiera się na fakcie, że ładunek netto w przewodach i komponentach jest stały.

Używa

Matrycowa wersja aktualnego prawa Kirchhoffa jest podstawą większości programów do symulacji obwodów , takich jak SPICE . Bieżące prawo jest używane z prawem Ohma do przeprowadzania analizy węzłowej .

Obecne prawo ma zastosowanie do każdej sieci skupionej, niezależnie od charakteru sieci; czy jednostronny czy dwustronny, aktywny czy pasywny, liniowy czy nieliniowy.

Prawo napięciowe Kirchhoffa

Suma wszystkich napięć wokół pętli jest równa zeru. v ₁ + v ₂ + v ₃ + v ₄ = 0

Prawo to, zwane także drugim prawem Kirchhoffa lub regułą pętli Kirchhoffa , brzmi następująco:

Ukierunkowana suma różnic potencjałów (napięć) wokół dowolnej zamkniętej pętli wynosi zero.

Podobnie jak obecne prawo Kirchhoffa, prawo napięciowe można zapisać jako:

$${\ Displaystyle \ suma _ {k = 1} ^ {n} V_ {k} = 0}$$

Tutaj n jest całkowitą liczbą zmierzonych napięć.

Wyprowadzenie prawa napięciowego Kirchhoffa

Podobne wyprowadzenie można znaleźć w The Feynman Lectures on Physics, tom II, rozdział 22: AC Circuits .

Rozważ dowolny obwód. Przybliż obwód z elementami skupionymi, tak aby (zmienne w czasie) pola magnetyczne były zawarte w każdym elemencie, a pole w obszarze na zewnątrz obwodu było pomijalne. Opierając się na tym założeniu, ujawnia to równanie Maxwella-Faradaya

$${\ Displaystyle \ nabla \ razy \ mathbf {E} = - {\ Frac {\ częściowy \ mathbf {B}} {\ częściowy t}} = \ mathbf {0}}$$

w obszarze zewnętrznym. Jeśli każdy ze składników ma skończoną objętość, to obszar zewnętrzny jest po prostu połączony , a zatem pole elektryczne jest w tym obszarze zachowawcze . Dlatego dla dowolnej pętli w obwodzie znajdujemy to

$$V_ {i} = - \ suma _ {i} \ int _ {{\ mathcal {P}}_{i}}\mathbf {E} \cdot \mathrm {d} \mathbf {l} =\oint \mathbf {E} \cdot \mathrm {d} \mathbf {l} = 0}$$

gdzie $.$ ścieżkami na zewnątrz każdego z komponentów, od jednego terminala do

Zauważ, że to wyprowadzenie wykorzystuje następującą definicję wzrostu napięcia od za $\ displaystyle a}$ do ${\ displaystyle b}$ : za {\ displaystyle a}

$${\ Displaystyle V_ {a \ do b} = - \ int _ {{\ mathcal {P}} _ {a \ do b}} \ mathbf {E } \cdot \mathrm {d} \mathbf {l} }$$

Jednak potencjał elektryczny (a tym samym napięcie) można zdefiniować na inne sposoby, na przykład poprzez rozkład Helmholtza .

Uogólnienie

W zakresie niskich częstotliwości spadek napięcia wokół dowolnej pętli wynosi zero. Obejmuje to wyimaginowane pętle rozmieszczone dowolnie w przestrzeni – nie ograniczając się do pętli wyznaczonych przez elementy obwodu i przewodniki. W zakresie niskich częstotliwości jest to następstwo prawa indukcji Faradaya (które jest jednym z równań Maxwella ).

Ma to praktyczne zastosowanie w sytuacjach związanych z „ elektrycznością statyczną ”.

Ograniczenia

Prawa obwodu Kirchhoffa są wynikiem modelu elementów skupionych i oba zależą od tego, czy model ma zastosowanie do danego obwodu. Gdy model nie ma zastosowania, przepisy nie mają zastosowania.

Obecne prawo opiera się na założeniu, że ładunek netto w dowolnym przewodzie, złączu lub elemencie skupionym jest stały. Ilekroć pole elektryczne między częściami obwodu jest nie do pominięcia, na przykład gdy dwa przewody są sprzężone pojemnościowo , może tak nie być. Dzieje się tak w obwodach prądu przemiennego o wysokiej częstotliwości, w których model elementów skupionych nie ma już zastosowania. Na przykład w linii transmisyjnej gęstość ładunku w przewodniku może się ciągle zmieniać.

W linii przesyłowej ładunek netto w różnych częściach przewodnika zmienia się w czasie. W bezpośrednim sensie fizycznym narusza to KCL.

Z drugiej strony prawo napięciowe opiera się na fakcie, że działanie zmiennych w czasie pól magnetycznych ogranicza się do poszczególnych elementów, takich jak cewki indukcyjne. W rzeczywistości indukowane pole elektryczne wytwarzane przez cewkę indukcyjną nie jest ograniczone, ale pola wycieku są często pomijalne.

Modelowanie rzeczywistych obwodów z elementami skupionymi

Przybliżenie elementu skupionego dla obwodu jest dokładne przy niskich częstotliwościach. Przy wyższych częstotliwościach znaczące stają się wyciekające strumienie i zmienne gęstości ładunków w przewodnikach. Do pewnego stopnia nadal możliwe jest modelowanie takich obwodów przy użyciu komponentów pasożytniczych . Jeśli częstotliwości są zbyt wysokie, bardziej odpowiednie może być bezpośrednie symulowanie pól przy użyciu modelowania metodą elementów skończonych lub innych technik .

Aby modelować obwody tak, aby nadal można było używać obu praw, ważne jest zrozumienie różnicy między fizycznymi elementami obwodu a idealnymi elementami skupionymi. Na przykład drut nie jest idealnym przewodnikiem. W przeciwieństwie do idealnego przewodnika, przewody mogą łączyć się ze sobą indukcyjnie i pojemnościowo (i ze sobą) oraz mają skończone opóźnienie propagacji. Rzeczywiste przewodniki można modelować w kategoriach elementów skupionych, biorąc pod uwagę pojemności pasożytnicze rozłożone między przewodami w celu modelowania sprzężenia pojemnościowego lub pasożytniczych (wzajemnych) indukcyjności modelować sprzężenie indukcyjne. Przewody mają również pewną indukcyjność własną.

Przykład

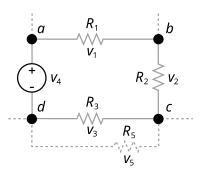
Załóżmy, że sieć elektryczna składa się z dwóch źródeł napięcia i trzech rezystorów.

Zgodnie z pierwszym prawem:

$${\ Displaystyle i_ {1} -i_ {2} -i_ {3} = 0}$$

Stosując drugie prawo do obwodu zamkniętego s ₁ i podstawiając napięcie za pomocą prawa Ohma otrzymujemy:

$${\ Displaystyle -R_ {2}i_ {2} + {\ mathcal {E}} _ {1} -R_ {1}i_ {1}=0}$$

Drugie prawo, ponownie połączone z prawem Ohma, zastosowane do obwodu zamkniętego s ₂ daje:

$${\ Displaystyle -R_ {3} i_ {3} - {\ mathcal {E}} _ {2} - {\ mathcal {E}} _ {1}+R_{2}i_{2}=0}$$

Daje to układ równań liniowych w i ₁ , i ₂ , i ₃ :

$${\ Displaystyle {\ rozpocząć {przypadki} i_ {1} -i_ {2} -i_ {3} & = 0 \\ - R_ {2} i_ {2} + {\ mathcal {E}} _ {1} - R_{1}i_{1}&=0\\-R_{3}i_{3}-{\mathcal {E}}_{2}-{\mathcal {E}}_{1}+R_{2 }i_{2}&=0\end{przypadki}}}$$

co jest równoważne

$${\ Displaystyle {\ rozpocząć {przypadki} i_ {1} + (-i_ {2}) + (-i_ {3}) & = 0 \\ R_ {1} i_ {1} + R_ {2} i_ {2 }+0i_{3}&={\mathcal {E}}_{1}\\0i_{1}+R_{2}i_{2}-R_{3}i_{3}&={\mathcal {E }}_{1}+{\mathcal {E}}_{2}\end{przypadki}}}$$

Zarozumiały

$${\ Displaystyle {\ rozpocząć {wyrównane} R_ {1} i = 100 \ Omega, & R_ { 2}&=200\Omega ,&R_{3}&=300\Omega ,\\{\mathcal {E}}_{1}&=3{\text{V}},&{\mathcal {E}} _{2}&=4{\text{V}}\end{wyrównane}}}$$

rozwiązaniem jest

$${\ Displaystyle {\ rozpocząć {przypadki} i_ {1} = {\ Frac {1} {1100}} {\ tekst {A} }\\[6pt]i_{2}={\frac {4}{275}}{\text{A}}\\[6pt]i_{3}=-{\frac {3}{220}}{ \text{A}}\end{przypadki}}}$$

Prąd i ₃ ma znak ujemny, co oznacza, że ​​przyjęty kierunek i ₃ był błędny i faktycznie i ₃ płynie w kierunku przeciwnym do czerwonej strzałki oznaczonej i ₃ . Prąd w R ₃ płynie od lewej do prawej.

Zobacz też

• Prawo indukcji Faradaya
• Dyscyplina skupionej materii

•   Paweł, Clayton R. (2001). Podstawy analizy obwodów elektrycznych . John Wiley & Synowie. ISBN 0-471-37195-5 .
•   Serway, Raymond A.; Jewett, John W. (2004). Fizyka dla naukowców i inżynierów (wyd. 6) . Brooks/Cole. ISBN 0-534-40842-7 .
•   Tipler, Paweł (2004). Fizyka dla naukowców i inżynierów: elektryczność, magnetyzm, światło i podstawowa fizyka współczesna (wyd. 5) . WH Freemana. ISBN 0-7167-0810-8 .
•   Graham, Howard Johnson, Martin (2002). Propagacja sygnału o dużej szybkości: zaawansowana czarna magia (wyd. 10. druk). Upper Saddle River, NJ: Prentice Hall PTR. ISBN 0-13-084408-X .

Linki zewnętrzne

• Rozdział Obwody dzielnika i prawa Kirchhoffa z lekcji w obwodach elektrycznych, tom 1, darmowy ebook DC i seria Lekcje w obwodach elektrycznych