Równanie Butlera-Volmera

W elektrochemii równanie Butlera -Volmera (nazwane na cześć Johna Alfreda Valentine'a Butlera i Maxa Volmera ), znane również jako równanie Erdeya-Grúza -Volmera , jest jednym z najbardziej podstawowych związków w kinetyce elektrochemicznej . Opisuje, w jaki sposób prąd elektryczny płynący przez elektrodę zależy od różnicy napięcia między elektrodą a elektrolitem w masie dla prostej, jednocząsteczkowej reakcji redoks, biorąc pod uwagę, że zarówno reakcja katodowa, jak i anodowa zachodzą na tej samej elektrodzie :

Równanie Butlera-Volmera

₀ Górny wykres przedstawia gęstość prądu w funkcji nadpotencjału η . Gęstości prądu anodowego i katodowego są pokazane jako j _a i j _c , odpowiednio dla α=α _a = α _c = 0,5 i j = 1mAcm ^-2 (bliskie wartości dla platyny i palladu). Dolny wykres przedstawia wykres logarytmiczny dla różnych wartości α (wykres Tafela)

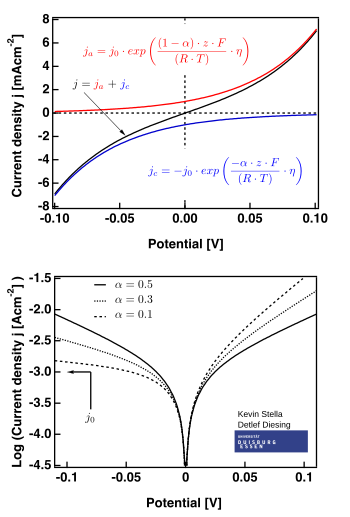
Równanie Butlera-Volmera to:

${\ Displaystyle j = j_ {0 }\cdot \left\{\exp \left[{\frac {\alpha _{\rm {a}}zF}{RT}}(E-E_{\rm {równ.}})\right]-\exp \left[-{\frac {\alpha _{\rm {c}}zF}{RT}}(E-E_{\rm {równ.}})\right]\right\}}$

lub w bardziej zwartej formie:

${\ Displaystyle j = j_ {0} \ cdot \ lewo \ {\ exp \ lewo [ {\frac {\alpha _{\rm {a}}zF\eta }{RT}}\right]-\exp \left[-{\frac {\alpha _{\rm {c}}zF\eta} {RT}}\prawo]\prawo\}}$

Gdzie:

• ${\ Displaystyle j}$ : gęstość prądu elektrody , A/m ² (zdefiniowana jako j = I/S )
• ${\ Displaystyle j_ {0}}$ : wymiana gęstości prądu , A / m ²
• ${\ displaystyle E}$ : potencjał elektrody , V
• $\ Displaystyle E _ {\ rm {równ.}}}$ : potencjał równowagi, V
• ${\ displaystyle T}$ : temperatura bezwzględna , K
• ${\ displaystyle z}$ : liczba elektronów biorących udział w reakcji elektrodowej
• ${\ displaystyle F}$ : stała Faradaya
• ${\ displaystyle R}$ : uniwersalna stała gazowa
• ${\ Displaystyle \ alpha _ {\ rm {c}}}$ : tak zwany współczynnik przenoszenia ładunku katodowego , bezwymiarowy
• ${\ Displaystyle \ alpha _ {\ rm {a}}}$ : tak zwany anodowy współczynnik przenoszenia ładunku, bezwymiarowy
• ${\ Displaystyle \ eta}$ : nadpotencjał aktywacji (zdefiniowany jako ${\ Displaystyle \ eta = EE_ {\ rm {równ.}}})$ .

Rysunek po prawej stronie pokazuje wykresy ważne dla ${\ Displaystyle \ alpha _ {\ rm {a}} = 1-\ alfa _ {\ rm {c}}}$ .

Przypadki graniczne

Istnieją dwa ograniczające przypadki równania Butlera-Volmera:

• obszar niskiego nadpotencjału (zwany „oporem polaryzacji”, tj. gdy mi ≈ mi _eq ), gdzie równanie Butlera-Volmera upraszcza się do:

${\ Displaystyle j = j_ { 0}{\frac {zF}{RT}}(E-E_{\rm {równ.}})}$ ;

• obszar wysokiego nadpotencjału, w którym równanie Butlera-Volmera upraszcza się do równania Tafela . Kiedy ${\ Displaystyle (E-E _ {\ rm {równ.}})>> 0}$ , dominuje pierwszy wyraz, a kiedy ${\ displaystyle ( ( E-E_{\rm {eq}})<<0}$ , dominuje drugi wyraz.

$_$ _ mi << mi _eq lub mi -

${\ Displaystyle E_ {\ rm {eq}} = a_ {\ rm {a}}$ dla reakcji anodowej, gdy E >> E _równ

gdzie i są stałymi (dla danej reakcji i temperatury) i nazywane są $Tafela$$równania$ Teoretyczne wartości stałych równania Tafela są różne dla procesów katodowych i anodowych. Jednak nachylenie Tafela można zdefiniować jako: ${\ displaystyle b}$

${\ Displaystyle b = \ lewo ({\ Frac {\ częściowe E} {\ częściowe \ ln | I _ {\ rm {F}} | }}\right)_{c_{i},T,p}}$

gdzie ${\ Displaystyle I _ {\ rm {F}}}$ jest prądem faradajskim, wyrażonym jako ${\ Displaystyle I _ {\ rm {F}} = ja _ {\ rm {c}} + ja _ {\ rm {a}}}$ , będąc $cząstkowymi$ i anodowymi prądami i ${\ displaystyle I _ {\ rm {a}}} .$

Rozszerzone równanie Butlera-Volmera

Bardziej ogólną postać równania Butlera-Volmera, mającą zastosowanie do warunków, na które ma wpływ przenoszenie masy, można zapisać jako:

${\ Displaystyle j=j_{0}\left\{{\frac {c_{\rm {o}}(0,t)}{c_{\rm {o}}^{*}}}\exp \left[{\ frac {\alpha _{\rm {a}}zF\eta}{RT}}\right]-{\frac {c_{\rm {r}}(0,t)}{c_{\rm {r} }^{*}}}\exp \left[-{\frac {\alpha _{\rm {c}}zF\eta }{RT}}\right]\right\}}$

Gdzie:

• j to gęstość prądu, A/m ² ,
• c _o i c _r odnoszą się odpowiednio do stężenia związków, które mają ulec utlenieniu i redukcji,
• c(0,t) jest stężeniem zależnym od czasu w odległości zero od powierzchni elektrody.

Powyższa postać upraszcza się do konwencjonalnej (pokazanej na górze artykułu), gdy stężenie substancji elektroaktywnych na powierzchni jest równe stężeniu w masie.

Istnieją dwa wskaźniki, które określają zależność prąd-napięcie dla elektrody. Pierwszym z nich jest szybkość reakcji chemicznej na elektrodzie, która zużywa reagenty i wytwarza produkty. Jest to znane jako transferu ładunku . Drugi to szybkość dostarczania reagentów i usuwania produktów z obszaru elektrody w różnych procesach, w tym dyfuzji, migracji i konwekcji. Ta ostatnia jest znana jako przenoszenia masy . Te dwie szybkości określają stężenia reagentów i produktów na elektrodzie, które z kolei są przez nie określane. Najwolniejsza z tych szybkości określi ogólną szybkość procesu.

Proste równanie Butlera-Volmera zakłada, że ​​stężenia na elektrodzie są praktycznie równe stężeniom w masie elektrolitu, co pozwala na wyrażenie prądu wyłącznie jako funkcji potencjału. Innymi słowy, zakłada się, że szybkość przenoszenia masy jest znacznie większa niż szybkość reakcji i że reakcja jest zdominowana przez wolniejszą szybkość reakcji chemicznej. Pomimo tego ograniczenia użyteczność równania Butlera-Volmera w elektrochemii jest szeroka i często uważa się, że ma ono „centralne znaczenie w fenomenologicznej kinetyce elektrod”.

Rozszerzone równanie Butlera-Volmera nie przyjmuje tego założenia, ale raczej przyjmuje stężenia na elektrodzie jako podane, dając zależność, w której prąd jest wyrażany jako funkcja nie tylko potencjału, ale także danych stężeń. Szybkość przenoszenia masy może być stosunkowo niewielka, ale jej jedyny wpływ na reakcję chemiczną wynika z zmienionych (danych) stężeń. W efekcie stężenia są również funkcją potencjału. Pełne traktowanie, które daje prąd tylko jako funkcję potencjału, zostanie wyrażone przez rozszerzone równanie Butlera-Volmera, ale będzie wymagało wyraźnego uwzględnienia efektów przenoszenia masy w celu wyrażenia stężeń jako funkcji potencjału.

Pochodzenie

Wyrażenie ogólne

Wykres różnych energii Gibbsa w funkcji współrzędnych reakcji. Reakcja będzie przebiegać w kierunku niższej energii - redukując dla krzywej niebieskiej, utleniając dla krzywej czerwonej. Zielona krzywa ilustruje równowagę.

Poniższe wyprowadzenie rozszerzonego równania Butlera-Volmera jest adaptacją wyprowadzenia Barda i Faulknera oraz Newmana i Thomasa-Alyei. Dla prostej jednocząsteczkowej, jednoetapowej reakcji postaci:

O+ne ⁻ → R

Prędkości reakcji do przodu i do tyłu ( v _f i v _b ) oraz, na podstawie praw elektrolizy Faradaya , związane z nimi gęstości prądu elektrycznego ( j ), można zapisać jako:

${\ Displaystyle v_ {f} = k_ {f} c_ {o} = j_ {f}/nF}$

${\ Displaystyle v_ {b} = k_ {b} c_ {r} = j_ {b}/nF}$

gdzie k _f i k _b to stałe szybkości reakcji , z jednostkami częstotliwości (1/czas), a c _o i c _r to stężenia powierzchniowe (mol/powierzchnia) odpowiednio utlenionej i zredukowanej cząsteczki (zapisane jako c _o ( 0,t) i c _r (0,t) w poprzedniej sekcji). Szybkość reakcji wypadkowej v i wypadkowa gęstość prądu j wynoszą zatem:

${\ Displaystyle v = v_ {b} -v_ {f} = {\ Frac {j_ {b} -j_ {f}} {nF }}={\frac {j}{nF}}}$

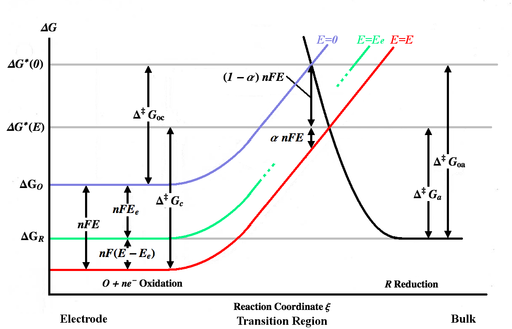
Powyższy rysunek przedstawia różne krzywe energii Gibbsa jako funkcję współrzędnej reakcji ξ. Współrzędna reakcji jest z grubsza miarą odległości, przy czym korpus elektrody znajduje się po lewej stronie, a roztwór masowy po prawej. Niebieska krzywa energii pokazuje wzrost energii Gibbsa dla utlenionej cząsteczki, gdy zbliża się ona do powierzchni elektrody, gdy nie jest przyłożony żaden potencjał. Krzywa czarnej energii pokazuje wzrost energii Gibbsa, gdy zredukowana cząsteczka zbliża się do elektrody. Dwie krzywe energii przecinają się w punkcie . ${\ Displaystyle \ Delta G ^ {*} (0)}$ . Przyłożenie potencjału E do elektrody przesunie krzywą energii w dół (do czerwonej krzywej) o nFE , a punkt przecięcia przesunie się do ${\ Displaystyle \ Delta G ^ {*} (E)}$ . $Displaystyle \ Delta ^ {\ ddagger} G_ {c}}$$za {\ Displaystyle \ Delta ^ {\ ddagger} G_ {a}}$ i to energie aktywacji (bariery energetyczne) do pokonania odpowiednio przez utlenione i zredukowane gatunki dla ogólnego mi , podczas gdy i ${\ Displaystyle \ Delta ^ {\ ddagger} G_ {oc}}$ i ${\ Displaystyle \ Delta ^ {\ ddagger} G_ {oa}}$ to energie aktywacji dla E=0 .

Załóżmy, że stałe szybkości są dobrze aproksymowane równaniem Arrheniusa ,

${\ Displaystyle k_ {f} = A_ {f} \ exp [- \ Delta ^ {\ ddagger} G_ {c} / RT]}$

${\ Displaystyle k_ {b} = A_ {b} \ exp [- \ Delta ^ {\ ddagger} G_ {a} / RT]}$

gdzie A _f i Ab _wyraz są takimi stałymi, że A _f c _o = A _b c _r jest „poprawnie zorientowaną” LUB częstotliwością kolizji, a wykładniczy (czynnik Boltzmanna) jest ułamkiem tych zderzeń o energii wystarczającej do pokonania barierę i reaguj.

Zakładając, że krzywe energii są praktycznie liniowe w obszarze przejściowym, można je tam przedstawić za pomocą:

$do {\ Displaystyle \ Delta G = S_ {c} \ xi + K_ {c}$	(niebieska krzywa)
${\ Displaystyle \ Delta G = S_ {c} \ xi + K_ {c} -nFE}$	(czerwona krzywa)
${\ Displaystyle \ Delta G = -S_ {a} \ xi + K_ {a}}$	(czarna krzywa)

Współczynnik przenoszenia ładunku w tym prostym przypadku jest równoważny współczynnikowi symetrii i można go wyrazić za pomocą nachyleń krzywych energii:

${\ Displaystyle \ alfa = {\ Frac {S_ {c}} {S_ {a} + S_ {c}}}}$

Wynika, że:

${\ Displaystyle \ Delta ^ {\ ddagger} G_ {c} = \ Delta ^ {\ ddagger} G_ {oc} + \ alfa nFE}$

${\ Displaystyle \ Delta ^ {\ ddagger} G_ {a} = \ Delta ^ {\ ddagger} G_ {oa} - (1- \ alfa) nFE}$

Dla zwięzłości zdefiniuj:

${\ Displaystyle f _ {\ alfa} = \ alfa nF / RT}$

${\ Displaystyle f _ {\ beta} = (1- \ alfa) nF / RT}$

${\ Displaystyle f = f _ {\ alfa} + f _ {\ beta} = nF/RT}$

Stałe szybkości można teraz wyrazić jako:

$^ {-f _ {\ alfa} E}}$

${\ Displaystyle k_ { b}=k_{bo}e^{f_{\beta}E}}$

gdzie stałe szybkości przy zerowym potencjale to:

${\ Displaystyle k_ {fo} = A_ {f} e ^ {- \ Delta ^ {\ ddagger} G_ {oc} / RT}}$

${\ Displaystyle k_ {bo} = A_ {b} e ^ {- \ Delta ^ {\ ddagger} G_ {oa} / RT}}$

Gęstość prądu j jako funkcję przyłożonego potencjału E można teraz zapisać:

${\ Displaystyle j = nF (c_ {r} k_ {bo} e ^ {f_ {\ beta} E }-c_{o}k_{fo}e^{-f_{\alfa }E})}$

Wyrażenie w kategoriach potencjału równowagi

Przy pewnym napięciu E _e równowaga zostanie osiągnięta, a prędkości do przodu i do tyłu ( v _f i v _b ) będą równe. Jest to reprezentowane przez zieloną krzywą na powyższym rysunku. Stałe szybkości równowagi będą zapisywane jako k _fe i k _be , a stężenia równowagi będą zapisywane jako c _oe i c _re . Prądy równowagi ( j _ce i j _ae ) będą równe i są zapisywane jako j _o , co jest znane jako gęstość prądu wymiany .

${\ Displaystyle v_ {fe} = k_ {fe} c_ {oe} = j_ {o}/nF$

${\ Displaystyle v_ {być} = k_ {być} c_ {re} = j_ {o}/nF}$

Zauważ, że wypadkowa gęstość prądu w stanie równowagi będzie równa zeru. Stałe szybkości równowagi wynoszą zatem:

${\ Displaystyle k_ {fe} = k_ {fo} e ^ {- f _ {\ alfa} E_ {e}}}$

${\ Displaystyle k_ {być} = k_ {bo} e ^ {f_ {\ beta} E_ {e}}}$

Rozwiązując powyższe dla k _fo i k _bo ze względu na stężenia równowagowe c _oe i c _re oraz gęstość prądu wymiany j _o , gęstość prądu j jako funkcję przyłożonego potencjału E można teraz zapisać:

$= j_ {o} \ lewo ({$

$\ Displaystyle c_ {$ w roztworze masowym, przy stężeniach i $} ^ {*}}$${\ Displaystyle c_ {oe} = c_ {o} ^ {*}}$ , wynika z tego, że i $Displaystyle c_ {re} = c_ {r} ^ {*}}$ i powyższe wyrażenie dla gęstości prądu j jest więc równaniem Butlera-Volmera. Należy zauważyć, że EE _{e jest również znane jako η,} nadpotencjał aktywacji .

Wyrażanie w kategoriach potencjału formalnego

Dla prostej reakcji zmiana energii Gibbsa to:

$Displaystyle \ Delta G = \ Delta G_ {o} - \ Delta G_{r}=(\Delta G_{o}^{o}-\Delta G_{r}^{o})+RT\ln \left({\frac {a_{oe}}{a_{re} }}\Prawidłowy)}$

gdzie a _oe i re _są czynnościami w równowadze . Aktywności a są powiązane ze stężeniami c przez a=γc, gdzie γ jest współczynnikiem aktywności . Potencjał równowagi jest określony równaniem Nernsta :

${\ Displaystyle E_ {e} = - {\ Frac {\ Delta G} {nF}} = E ^ {o}+{\frac {RT}{nF}}\ln \left({\frac {a_{oe}}{a_{re}}}\right)}$

gdzie $_$ potencjałem _

${\ Displaystyle E ^ {o} = - (\ Delta G_ {o} ^ {o} - \ Delta G_ {r} ^ {o} )/nF}$

Definiowanie potencjału formalnego :

${\ Displaystyle E ^ {o'} = E ^ {o} + {\ Frac {RT} {nF}} \ ln \ left({\frac {\gamma _{oe}}{\gamma _{re}}}\right)}$

potencjał równowagi wynosi wtedy:

${\ Displaystyle E_ {e} = E ^ {o '} + {\ Frac {RT} {nF}} \ ln \ lewo ({\frac {c_{oe}}{c_{re}}}\right)}$

Podstawienie tego potencjału równowagi do równania Butlera-Volmera daje:

$\ Displaystyle j = {\ Frac {j_{o}}{c_{oe}^{1-\alpha}c_{re}^{\alpha}}}\left(c_{r}e^{f_{\beta}(EE^{o' })}-c_{o}e^{-f_{\alpha}(EE^{o'})}\right)}$

co można również zapisać w postaci stałej szybkości standardowej k ^o jako:

${\ Displaystyle j = nFk ^ {o} \ lewo (c_ {r }e^{f_{\beta }(EE^{o'})}-c_{o}e^{-f_{\alpha }(EE^{o'})}\right)}$

Standardowa stała szybkości jest ważnym deskryptorem zachowania elektrody, niezależnym od stężeń. Jest miarą szybkości, z jaką system zbliża się do stanu równowagi. $będzie$ granicy jako elektroda staje się idealną elektrodą polaryzowalną i zachowywać się elektrycznie jak obwód otwarty (pomijając pojemność). W przypadku prawie idealnych elektrod o małym ^ko wymagane są duże zmiany nadpotencjału, aby wygenerować znaczny prąd. $będzie$ granicy jako elektroda staje się idealną elektrodą niepolaryzowalną zachowywać się jak zwarcie elektryczne. W przypadku prawie idealnych elektrod o dużym ko ^. małe zmiany nadpotencjału będą generować duże zmiany prądu

Zobacz też

• Zaawansowana biblioteka symulacji
• Równanie Nernsta
• Równanie Goldmana
• Równanie Tafela

Linki zewnętrzne

• Media związane z równaniem Butlera-Volmera w Wikimedia Commons