Równanie wzrostu pęknięć

Rysunek 1: Typowy wykres szybkości wzrostu pęknięć w funkcji zakresu intensywności naprężeń. Równanie Paryża -Erdogana pasuje do centralnego regionu liniowego reżimu B.

Równanie wzrostu pęknięcia służy do obliczania rozmiaru pęknięcia zmęczeniowego powstającego pod wpływem obciążeń cyklicznych. Rozwój pęknięć zmęczeniowych może doprowadzić do katastrofalnej w skutkach awarii, szczególnie w przypadku samolotów. Równanie wzrostu pęknięć można wykorzystać do zapewnienia bezpieczeństwa, zarówno w fazie projektowania, jak i podczas eksploatacji, poprzez przewidywanie wielkości pęknięć. W konstrukcji krytycznej obciążenia można rejestrować i wykorzystywać do przewidywania wielkości pęknięć, aby zapewnić konserwację lub wycofanie z eksploatacji przed uszkodzeniem któregokolwiek z pęknięć.

Trwałość zmęczeniową można podzielić na okres inicjacji i okres wzrostu pęknięć. Równania wzrostu pęknięć są wykorzystywane do przewidywania wielkości pęknięć począwszy od danej początkowej skazy i zazwyczaj opierają się na danych doświadczalnych uzyskanych z testów zmęczeniowych przy stałej amplitudzie .

$równanie$ z najwcześniejszych równań wzrostu pęknięć opartych na zakresie intensywności naprężeń w cyklu obciążenia ( ) jest Parisa-Erdogana

${\ Displaystyle {da \ nad dN} = C (\ Delta K) ^ {m}}$

gdzie ${\ Displaystyle a} to$${\ rm {d}} a / {\ rm {d}$ pęknięcia i wzrost pęknięcia zmęczeniowego dla pojedynczego cyklu obciążenia $} \displaystyle N}$ . Opracowano różne równania wzrostu pęknięć podobne do równania Parisa-Erdogana, aby uwzględnić czynniki wpływające na tempo wzrostu pęknięć, takie jak współczynnik naprężeń, przeciążenia i skutki historii obciążeń.

Zakres intensywności stresu można obliczyć z maksymalnego i minimalnego natężenia stresu dla cyklu

${\ Displaystyle \ Delta K = K _ {\ tekst {maks.}} - K _ {\ tekst {min}}}$

Współczynnik geometrii jest używany do powiązania naprężenia pola dalekiego z intensywnością naprężenia wierzchołka pęknięcia za pomocą $sigma}$$displaystyle$

${\ Displaystyle K = \ beta \ sigma {\ sqrt {\ pi a}}}$ .

Istnieją standardowe odniesienia zawierające współczynniki geometrii dla wielu różnych konfiguracji.

Historia równań propagacji pęknięć

Na przestrzeni lat zaproponowano wiele równań propagacji pęknięć, aby poprawić dokładność prognoz i uwzględnić różnorodne efekty. Prace Heada, Frosta i Dugdale'a, McEvily'ego i Illga oraz Liu dotyczące zachowania pęknięć zmęczeniowych położyły podwaliny pod ten temat. Ogólną postać tych równań propagacji pęknięć można wyrazić jako

${\ Displaystyle {da \ nad dN} = f (\ Delta \ sigma, a, C_ {i}),}$

$\ Delta \ sigma}$ długość pęknięcia jest oznaczona przez $,$ zastosowanych cykli obciążenia jest określona przez , zakres naprężeń przez $Displaystyle$ , a materiał parametry przez do $\ displaystyle C_ {i}}$ . $konfiguracji$ symetrycznych długość pęknięcia od linii symetrii jest definiowana jako $i$ całkowitej długości pęknięcia .

$,$ w postaci są prawdziwym równaniem różniczkowym nie modelują procesu wzrostu pęknięć w sposób ciągły przez cały cykl Jako takie, osobne algorytmy zliczania cykli lub identyfikacji, takie jak powszechnie stosowany algorytm zliczania opadów deszczu , są wymagane do określenia wartości maksymalnych i minimalnych w cyklu. Chociaż wykazano, że zliczanie opadów deszczu zostało opracowane z myślą o metodach naprężeń / odkształceń, które również działają w przypadku wzrostu pęknięć. Opracowano również niewielką liczbę rzeczywistych równań wzrostu pęknięć zmęczeniowych pochodnych.

Czynniki wpływające na tempo wzrostu pęknięć

reżimy

$.$ typowy wykres tempa wzrostu pęknięć w funkcji zmiennego natężenia naprężeń lub siły napędowej wierzchołka pęknięcia na skali logarytmicznej Zachowanie szybkości wzrostu pęknięć w odniesieniu do zmiennego natężenia naprężeń można wyjaśnić w różnych reżimach (patrz rysunek 1) w następujący sposób

Reżim A: Przy niskich szybkościach wzrostu zmiany w mikrostrukturze , średnim naprężeniu (lub stosunku obciążenia) i środowisku mają znaczący wpływ na szybkość propagacji pęknięć. Obserwuje się, że przy niskich współczynnikach obciążenia szybkość wzrostu jest najbardziej wrażliwa na mikrostrukturę, aw materiałach o niskiej wytrzymałości jest najbardziej wrażliwa na współczynnik obciążenia.

Reżim B: W średnim zakresie tempa wzrostu zmiany mikrostruktury, średniego naprężenia (lub współczynnika obciążenia), grubości i środowiska nie mają znaczącego wpływu na szybkość propagacji pęknięć.

Reżim C: Przy dużych szybkościach wzrostu propagacja pęknięć jest bardzo wrażliwa na zmiany mikrostruktury, średniego naprężenia (lub współczynnika obciążenia) i grubości. Skutki środowiskowe mają stosunkowo mniejszy wpływ.

Efekt współczynnika stresu

Cykle o wyższym współczynniku naprężeń ${\ Displaystyle R = K _ {\ tekst {min}}}/ {K _ {\ tekst {max}} \ równoważnik P _ {\ tekst {min }}/{P_{\text{max}}}}$ mają zwiększone tempo wzrostu pęknięć. Efekt ten jest często wyjaśniany za pomocą zamykania pęknięć , która opisuje obserwację, że powierzchnie pęknięć mogą pozostawać w kontakcie ze sobą przy obciążeniach powyżej zera. Zmniejsza to efektywny zakres współczynnika intensywności naprężeń i tempo wzrostu pęknięć zmęczeniowych.

Efekty sekwencyjne

ZA ${\ displaystyle da/dN}$ Równanie podaje tempo wzrostu dla pojedynczego cyklu, ale gdy obciążenie nie ma stałej amplitudy, zmiany obciążenia mogą prowadzić do tymczasowych wzrostów lub spadków tempa wzrostu. Aby rozwiązać niektóre z tych przypadków, opracowano dodatkowe równania. Tempo wzrostu jest spowolnione, gdy w sekwencji ładowania wystąpi przeciążenie. Obciążenia te generują strefy plastyczne, które mogą opóźniać tempo wzrostu. Dwa godne uwagi równania do modelowania opóźnień występujących podczas narastania pęknięcia w obszarze przeciążenia to:

Model Wheelera (1972)

${\ Displaystyle \ lewo ({\ Frac {da} {dN}} \ prawej) _ {\ tekst {VA}} = \ beta \ lewo ({\ Frac {da} {dN}} \ prawo) _ {\ tekst {CA}}} z β$ = $Displaystyle \ beta = \ lewo ({\ frac { r_{\text{pi}}}{r_{\text{max}}}}\right)^{k}}$

gdzie ${\ displaystyle r _ {\ tekst {pi}}}$ jest strefą plastyczną odpowiadającą i-temu cyklowi, który występuje po przeciążeniu, a ${\ displaystyle r_ {\ tekst {max}}}$ jest odległością między pęknięciem oraz zasięg strefy plastycznej przy przeciążeniu.

modelu Willenborga

Równania wzrostu pęknięć

Równanie progowe

Do przewidywania tempa wzrostu pęknięć w rejonie progowym wykorzystano następującą zależność

${\ Displaystyle {da \ nad dN} = A \ lewo (\ Delta K- \ Delta K _ {\ tekst {th}} \ prawo) ^ {p}.}$

Równanie Paryża-Erdoğana

Do przewidywania tempa wzrostu pęknięć w reżimie pośrednim wykorzystuje się równanie Parisa-Erdoğana

${\ Displaystyle {da \ nad dN} = C \ lewo (\ Delta K \ prawo) ^ {m}.}$

Równanie Formana

W 1967 roku Forman zaproponował następującą zależność, aby uwzględnić zwiększone tempo wzrostu spowodowane współczynnikiem naprężeń i zbliżaniem się do odporności na ${\ Displaystyle K _ {\ tekst {c}}}$ K

${\ Displaystyle {da \ nad dN} = {\ Frac {C (\ Delta K) ^ {n}} {(1- R)K_{\text{c}}-\Delta K}}}$

Równanie McEvily'ego-Groegera

McEvily i Groeger zaproponowali następujący związek mocy, który uwzględnia skutki zarówno wysokich, jak i niskich wartości ${\ Displaystyle \ Delta K}$

${\ Displaystyle {da \ nad dN} = A (\ Delta K- \ Delta K _ {\ tekst {th }})^{2}{\Duży [}1+{\frac {\Delta K}{K_{\text{Ic}}-K_{\text{max}}}}{\Big ]}}$ .

równanie NASGRO

Równanie NASGRO jest używane w programach wzrostu pęknięć AFGROW, FASTRAN i NASGRO. Jest to ogólne równanie, które obejmuje niższą szybkość wzrostu w pobliżu progu $i$$.$ wzrostu zbliżającą się do , a także uwzględnienie średniego efektu naprężenia poprzez włączenie współczynnika naprężeń. ${\ displaystyle R}$ . Równanie NASGRO jest

${\ Displaystyle {\ Frac {da} {dN}} = C \ lewo [\ lewo ({\ Frac {1-f} {1-R}} \ prawej) \ Delta K \ prawej] ^ {n} {\ left(1-{\frac {\Delta K_{\text{th}}}{\Delta K}}\right)^{p} \over \left(1-{\frac {K_{\max}}{ K_{\text{crit}}}}\right)^{q}}}$

gdzie do ${\ Displaystyle C}$ fa $\ Displaystyle f}$ , ${\ Displaystyle n}$ , ${\ Displaystyle p}$ , ${\ Displaystyle q}$ , ${\ Displaystyle \ Delta K _ {\ tekst {th }}}$ i ${\ displaystyle K _ {\ text {crit}}}$ to współczynniki równania.

Równanie McClintocka

W 1967 roku McClintock opracował równanie na górną granicę wzrostu pęknięcia w oparciu o cykliczne przemieszczenie otwarcia wierzchołka pęknięcia. ${\ Displaystyle \ Delta {\ tekst {CTOD}}}$

${\ Displaystyle {da \ nad dN} \ propto \ Delta {\ tekst {CTOD}} \ około \ beta {(\ Delta K) ^ { 2} \ponad {2\sigma _{0}E'}}}$

gdzie jest naprężeniem płynięcia, $jest$$jest stałą$$Younga$ i w zakresie

Równanie Walkera

Aby uwzględnić efekt współczynnika stresu, Walker zasugerował zmodyfikowaną postać równania Parisa-Erdogana

${\ Displaystyle {da \ nad dN} = C {\ Big (} {\ overline {\ Delta K}}} {\ Big)} ^ {m} = C {\ bigg (} {\ Frac {\ Delta K} (1-R)^{1-\gamma }}}{\bigg )}^{m}=C{\big (}K_{\text{max}}(1-R)^{\gamma }{\ duży )}^{m}}$

gdzie jest parametrem $,$ który reprezentuje wpływ stosunku naprężeń na szybkość wzrostu pęknięć zmęczeniowych. Zazwyczaj przyjmuje wartość około ${\ displaystyle 0,5}$$,$ ale może wahać się między $\ displaystyle 0,3-1,0}$ . Ogólnie przyjmuje się, że ściskająca część cyklu obciążenia nie ma wpływu na wzrost $uwagę$${\ Displaystyle \ gamma = 0,}$ co daje ${\ displaystyle {\ overline {\ Delta K}} = K _ {\ text {max}}.}$ Można to fizycznie wytłumaczyć, biorąc pod uwagę, że pęknięcie zamyka się przy zerowym obciążeniu i nie zachowuje się jak pęknięcie pod obciążeniem ściskającym. W bardzo plastycznych materiałach $,$ ściskające przyczynia się do wzrostu pęknięć zgodnie .

Równanie Elbera

$, aby umożliwić zamknięcie$ poprzez wprowadzenie poziomu intensywności naprężenia , przy którym następuje kontakt. Poniżej tego poziomu nie ma ruchu na wierzchołku pęknięcia, a zatem nie ma wzrostu. Efekt ten został wykorzystany do wyjaśnienia efektu współczynnika naprężeń i zwiększonego tempa wzrostu obserwowanego przy krótkich pęknięciach. Równanie Elbera jest

$-K _ {\ tekst {op}}} re$

${\ Displaystyle {da \ ponad dN} = C (\ Delta K _ {\ tekst {eff}}) ^ {m}}$

Równanie materiałów ciągliwych i kruchych

Ogólną postać szybkości wzrostu pęknięć zmęczeniowych w materiałach ciągliwych i kruchych podaje wzór

${\ Displaystyle {da \ nad dN} \ propto (K _ {\ tekst {max}}) ^ {n} (\ Delta K) ^ {p} ,}$

gdzie i $_$$parametrami$ . Opierając się na różnych mechanizmach posuwania się pęknięć i osłaniania wierzchołków pęknięć w metalach, ceramice i materiałach międzymetalicznych , obserwuje się, że tempo wzrostu pęknięć zmęczeniowych w metalach jest istotnie zależne od terminu, w ceramice od K. ${\ Displaystyle \ Delta K$${\ displaystyle K _ {\ text {max}}}$ , a związki międzymetaliczne mają prawie podobną zależność od i $}$ K ${\ Displaystyle K _ {\ tekst {max}}}$ warunki.

Prognozowanie życia zmęczeniowego

Programy komputerowe

Istnieje wiele programów komputerowych, które implementują równania wzrostu pęknięć, takie jak Nasgro , AFGROW i Fastran . Ponadto istnieją również programy realizujące probabilistyczne podejście do wzrostu pęknięć, które obliczają prawdopodobieństwo awarii w całym okresie eksploatacji elementu.

Programy wzrostu pęknięć zwiększają pęknięcie od początkowego rozmiaru wady, aż przekroczy odporność na pękanie materiału i zawiedzie. Ponieważ odporność na pękanie zależy od warunków brzegowych, odporność na pękanie może zmieniać się od płaskich odkształcenia dla półkolistego pęknięcia powierzchniowego do płaskich warunków naprężeń dla pęknięcia przelotowego. Odporność na kruche pękanie w płaskich warunkach naprężeń jest zwykle dwa razy większa niż w przypadku płaskich odkształceń. Jednak ze względu na szybkie tempo wzrostu pęknięcia pod koniec jego żywotności, wahania odporności na kruche pękanie nie wpływają znacząco na żywotność elementu.

Programy wzrostu pęknięć zazwyczaj zapewniają wybór:

• metody liczenia cykli w celu wyodrębnienia ekstremów cykli
• współczynniki geometrii, które dobierają kształt pęknięcia i przyłożone obciążenie
• równanie wzrostu pęknięć
• modele akceleracji/opóźnienia
• właściwości materiału, takie jak granica plastyczności i odporność na pękanie

Rozwiązanie analityczne

Współczynnik intensywności stresu jest określony przez

${\ Displaystyle K = \ beta \ sigma {\ sqrt {\ pi a}}}$

gdzie jest przyłożonym równomiernym naprężeniem rozciągającym działającym na próbkę w kierunku prostopadłym do płaszczyzny pęknięcia, $jest$$pęknięcia$ i jest bezwymiarowym parametrem, który jest $displaystyle \ sigma}$ zależy od geometrii próbki. Zmienia się intensywność naprężeń

${\ Displaystyle {\ rozpocząć {wyrównane} \ Delta K & = {\ rozpocząć {przypadki }\beta (\sigma _{\text{max}}-\sigma _{\text{min}}){\sqrt {\pi a}}=\beta \Delta \sigma {\sqrt {\pi a} },\qquad R\geq 0\\\beta \sigma _{\text{max}}{\sqrt {\pi a}},\qquad R<0\end{przypadki}},\end{wyrównane}} }$

gdzie $naprężeń$ zakresem cyklicznej amplitudy

Zakładając, że początkowy rozmiar pęknięcia wynosi $,$$uszkodzeniem$${ \ Displaystyle {\ duży (} K = K _ {\ tekst {maks.}} = K _ {\ tekst {Ic}} {\ duży)}}$ pęknięcia próbki można obliczyć za pomocą jak

${\ Displaystyle {\ rozpocząć {wyrównane} K _ {\ tekst {Ic}} & = \ beta \ sigma _ {\ tekst {max}}} {\ sqrt {\ pi a_ {c}}}, \\\ Strzałka w prawo a_ { c}&={\frac {1}{\pi}}{\bigg (}{\frac {K_{\text{Ic}}}{\beta \sigma _{\text{max}}}}{\ bigg )}^{2}.\end{wyrównane}}}$

Powyższe równanie $niejawny iw$ potrzeby można je rozwiązać numerycznie.

Przypadek I

Dla ${\ Displaystyle R \ geq 0,7,}$ zamknięcie pęknięcia ma znikomy wpływ na tempo wzrostu pęknięcia, a równanie Paris-Erdogan może być użyte do obliczenia trwałości zmęczeniowej próbki, zanim osiągnie ona krytyczny rozmiar pęknięcia ${\ displaystyle a_ {c}}$ jak

${\ Displaystyle {\ rozpocząć {wyrównane} {da \ nad dN} & = C (\ Delta K) ^ {m} = C {\ bigg (} \ beta \ Delta \ sigma {\ sqrt {\ pi a}} \bigg )}^{m},\\\Strzałka w prawo N_{f}&={\frac {1}{({\sqrt {\pi}}\Delta \sigma )^{m}}}\int _{ a_{0}}^{a_{c}}{\frac {da}{(C{\sqrt {a}}\beta)^{m}}}.\end{wyrównane}}}$

Model wzrostu pęknięć o stałej wartości 𝛽 i R = 0

Rysunek 2: Reprezentacja geometryczna próbki do badania rozciągania w środku pękniętego

W przypadku modelu wzrostu pęknięć Griffitha-Irwina lub pęknięcia środkowego o długości $za {\ displaystyle 2a}$$pokazano$ rysunku 2, mamy i jest niezależny od pęknięcia długość. Można również $, że jest niezależny od długości pęknięcia.$ Zakładając, że powyższa całka upraszcza się do ${\ Displaystyle \ beta = {\ tekst {stała}}$

$Displaystyle N_ {f} = {\ Frac {1} {C ({\ sqrt {\ pi}} \ beta \Delta \sigma )^{m}}}\int _{a_{0}}^{a_{c}}{\frac {da}{({\sqrt {a}})^{m}}}, }$

całkując powyższe wyrażenie dla przypadków i ${\ displaystyle$$m = 2}$ całkowita liczba cykli obciążenia jest dana przez m $}$

${\ Displaystyle {\ rozpocząć {wyrównane} N_ {f} & = {\ Frac {2} {(m-2) C ({\ sqrt {\ pi}} \ beta \Delta \sigma )^{m}}}{\Bigg [}{\frac {1}{(a_{0})^{\frac {m-2}{2}}}}-{\frac {1 }{(a_{c})^{\frac {m-2}{2}}}}{\Bigg ]},\qquad m\neq 2,\\N_{f}&={\frac {1} {\pi C(\beta \Delta \sigma )^{2}}}\ln {\frac {a_{c}}{a_{0}}},\qquad m=2.\end{wyrównane}}}$

Teraz, aby krytyczny rozmiar $pęknięcia$ był bardzo duży w porównaniu z początkowym rozmiarem pęknięcia ${0}{\big )}}$$\ Displaystyle {\ duży (} a_ {c}$ da

${\ Displaystyle N_ {f} = {\ Frac {2} {(m-2) C ({\ sqrt {\ pi}} \ Delta \ sigma \ beta) ^ {m}}} (a_ {0}) ^ {\frac {2-m}{2}}.}$

Powyższe wyrażenia analityczne dla całkowitej liczby cykli obciążenia do złamania $założeniu, że$ Y $Displaystyle Y = {\ tekst {stała}}}$ . W przypadkach, w których $pęknięcia, takich jak geometrie naprężenia karbu pojedynczej krawędzi (SENT),$ środkowego pękniętego (CCT), do obliczenia można zastosować całkowanie numeryczne. ${\ displaystyle N_ {f.}}$ .

Przypadek II

Ponieważ zjawisko $zamykania pęknięć ma wpływ na szybkość$ , aby obliczyć trwałość zmęczeniową próbki, zanim osiągnie ona krytyczny rozmiar pęknięcia za do $displaystyle a_{c}}$ jako

${\ Displaystyle {\ rozpocząć {wyrównane} {da \ nad dN} & = C {\ bigg (}{\ Frac {\ Delta K} {(1-R) ​​^ {1- \ gamma}}} {\ bigg) }^{m}={\frac {C}{(1-R)^{m(1-\gamma)}}}{\bigg (}\beta \Delta \sigma {\sqrt {\pi a}} {\bigg )}^{m},\\\strzałka w prawo N_{f}&={\frac {(1-R)^{m(1-\gamma)}}{({\sqrt {\pi}} \Delta \sigma )^{m}}}\int _{a_{0}}^{a_{c}}{\frac {da}{(C{\sqrt {a}}\beta)^{m} }}.\end{wyrównane}}}$

Obliczenia numeryczne

Rysunek 3: Schematyczne przedstawienie procesu przewidywania trwałości zmęczeniowej

$jest$ przydatny, gdy $zależy$ od . Początkowy rozmiar pęknięcia jest uważany za ${\ displaystyle a_ {0}}$ . Współczynnik intensywności naprężenia przy obecnym rozmiarze pęknięcia $obliczany$ przy użyciu maksymalnego przyłożonego naprężenia as

${max}} & = \ beta \ sigma _ {\ tekst {max}} {\ sqrt {\ pi a}}$${\ Displaystyle K _ {\ tekst {max}}}$ . jest mniejsza niż odporność na pękanie ${\ Displaystyle K _ {\ tekst {Ic}}}$ pęknięcie nie osiągnęło rozmiaru krytycznego $\ displaystyle a_ {c }}$ i symulacja jest kontynuowana z bieżącym rozmiarem pęknięcia, aby obliczyć intensywność naprężeń przemiennych jako

${\ Displaystyle \ Delta K = \ beta \ Delta \ sigma {\ sqrt {\ pi a}}.}$

Teraz, zastępując współczynnik intensywności naprężeń w równaniu Parisa-Erdogana, przyrost wielkości pęknięcia $za {\ displaystyle \ Delta a}$ się jako

${\ Displaystyle \ Delta a = C (\ Delta K) ^ {m} \ Delta N}$

gdzie jest rozmiar kroku cyklu ${\ displaystyle \ Delta N} .$ Nowy rozmiar pęknięcia staje się

${\ Displaystyle a_ {i + 1} = a_ {i} + \ Delta a,}$

gdzie indeks $się$ do bieżącego kroku iteracji. Nowy rozmiar pęknięcia jest używany do obliczenia intensywności naprężenia przy maksymalnym zastosowanym naprężeniu dla następnej iteracji. Ten iteracyjny proces jest kontynuowany aż

${\ Displaystyle K _ {\ tekst {maks.}} \ geq K _ {\ tekst {Ic}}.}$

Po spełnieniu tego kryterium zniszczenia symulacja jest zatrzymywana.

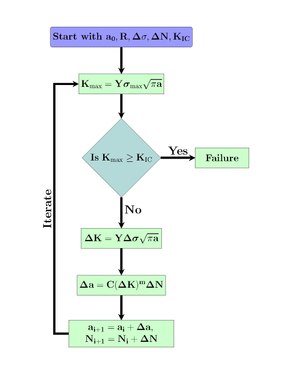
Schematyczne przedstawienie procesu prognozowania trwałości zmęczeniowej przedstawiono na rysunku 3.

Przykład

Rysunek 4: Reprezentacja geometryczna próbki do badania rozciągania z karbem pojedynczej krawędzi

Współczynnik intensywności naprężeń w próbce SENT (patrz rysunek 4) pod wpływem wzrostu pęknięć zmęczeniowych jest określony wzorem

${\ Displaystyle {\ rozpocząć {wyrównane} K_ {I} & = \ beta \ sigma {\ sqrt {\ pi a}} = \ sigma {\ sqrt {\ pi a}}} {\ Bigg [} 0,265 {\ bigg [ }1-{\frac {a}{W}}{\bigg ]}^{4}+{\frac {0.857+0.265{\frac {a}{W}}}{{\big [}1-{ \frac {a}{W}}{\big ]}^{\frac {3}{2}}}}{\Bigg ]},\\\Delta K_{I}&=K_{\text{max} }-K_{\text{min}}=\beta \Delta \sigma {\sqrt {\pi a}}.\end{wyrównane}}}$

Do obliczeń brane są pod uwagę następujące parametry

${\ Displaystyle a_ {0} = 5}$ mm, ${\ Displaystyle W = 100}$ mm, ${\ Displaystyle h = 200}$ mm, ${\ Displaystyle K_ { \text {Ic}} = 30 {\ text {MPa}} {\ sqrt {\ text {m}}}}, R = K min K max = 0,7 {\ Displaystyle R$ = ${ min}}}{K_{\text{maks}}}}=0,7}$ ,

${\ Displaystyle \ Delta \ sigma = 20}$ MPa, ${\ Displaystyle C = 4,6774 \ razy 10 ^ {- 11} {\ Frac {\ text{m}}{\text{cykl}}}{\frac {1}{({\text{MPa}}{\sqrt {\text{m}}})^{m}}}}$ , ${\ displaystyle m = 3,874}$ .

Krytyczną długość pęknięcia $=$ obliczyć, gdy $}}$ Jak

${\ Displaystyle a_ {c} = {\ Frac {1} {\ pi}} {\ Bigg (}{\ Frac {0,45} {\ beta}} {\ Bigg)} ^ {2}.}$

Rozwiązując powyższe równanie, $.$ długość

Teraz, powołując się na równanie Paris-Erdogan daje

${\ Displaystyle N_ {f} = {\ Frac {1} {C (\ Delta \ sigma) ^ {m} ({\ sqrt {\ pi}}) ^ {m}}} \ int _ {a_ {0} }^{a_{c}}{\frac {da}{a^{\frac {m}{2}}{\Bigg [}0,265{\bigg [}1-{\frac {a}{W}} {\bigg ]}^{4}+{\frac {0,857+0,265{\frac {a}{W}}}{{\big [}1-{\frac {a}{W}}{\big] }^{\frac {3}{2}}}}{\Bigg ]}^{m}}}}$

Poprzez numeryczne całkowanie powyższego wyrażenia, całkowitą liczbę cykli obciążenia do zniszczenia otrzymuje się jako ${\ Displaystyle N_ {f} = 1,2085 \ razy 10 ^ {6} {\ tekst {cykli}} }$ .

Linki zewnętrzne

• Forman, RG; Shivakumar, V.; Kardynał ŚJ; Williams, Kalifornia; McKeighan, PC (2005). „Baza danych wzrostu pęknięć zmęczeniowych do analizy tolerancji uszkodzeń” (PDF) . FAA . Źródło 6 lipca 2019 r .
• Gallagher, JP; Giessler, FJ; Berens, AP; Engle, Jr, JM „Podręcznik projektowania odpornego na uszkodzenia USAF: Wytyczne dotyczące analizy i projektowania konstrukcji samolotów odpornych na uszkodzenia. Wersja B” . Zarchiwizowane od oryginału w dniu 9 lipca 2019 r . Źródło 9 lipca 2019 r .
• „Podręcznik oceny tolerancji uszkodzeń, tom I: Wprowadzenie, mechanika pękania, propagacja pęknięć zmęczeniowych” (PDF) . Federalna Administracja Lotnictwa. 1993 . Źródło 16 lipca 2019 r .