Reguła Naismitha

Reguła Naismitha pomaga w planowaniu wyprawy pieszej lub pieszej , obliczając, ile czasu zajmie pokonanie zamierzonej trasy, w tym dodatkowy czas potrzebny na wejście pod górę. Ta praktyczna zasada została opracowana przez Williama W. Naismitha , szkockiego alpinistę , w 1892 roku. Nowoczesną wersję można sformułować w następujący sposób:

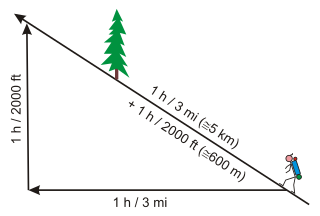
Przeznacz jedną godzinę na każde 3 mile (5 km) do przodu oraz dodatkową godzinę na każde 2000 stóp (600 m) wznoszenia.

Założenia i obliczenia

Tempo w minutach na kilometr lub milę vs. kąt nachylenia wynikający z reguły Naismitha dla prędkości bazowych 5 i 4 km/h.

Oryginalna zasada Naismitha z 1892 roku mówi, że na mapie należy przeznaczyć jedną godzinę na trzy mile i dodatkową godzinę na każde 2000 stóp wzniesienia. Jest to zawarte w ostatnim zdaniu jego relacji z wyjazdu.

Dziś jest formułowana na wiele sposobów. 1 h / 3 mi + 1 h / 2000 stóp Naismitha można zastąpić:

1 godzina / 3 mile (5 km) + 1 godzina / 2000 stóp (600 m)
1 godz. / 5 km (3 mil) + 1/2 godz. / 300 m (1000 stóp)
3 mph + ½ h / 1000 stóp 5 km/h + ½ h / 300 m
12 min / 1 km + 10 min / 100 m

Podstawowa zasada zakłada wędrowców o rozsądnej kondycji, w typowym terenie iw normalnych warunkach. Nie uwzględnia opóźnień, takich jak wydłużone przerwy na odpoczynek lub zwiedzanie, czy przeszkody nawigacyjne. Przy planowaniu wypraw lider zespołu może skorzystać z reguły Naismitha przy układaniu karty trasy . ^{[ potrzebne źródło ]}

Możliwe jest zastosowanie korekt lub „poprawek” dla bardziej wymagającego terenu, chociaż nie można ich używać do tras mieszanych . W systemie oceniania stosowanym w Ameryce Północnej reguła Naismitha ma zastosowanie tylko do podwyżek ocenionych jako klasa 1 w systemie dziesiętnym Yosemite , a nie do klasy 2 lub wyższej. ^{[ potrzebne źródło ]}

W praktyce wyniki reguły Naismitha są zwykle uważane za minimalny czas potrzebny do pokonania trasy. ^{[ potrzebne źródło ]}

Podczas chodzenia w grupach obliczana jest prędkość najwolniejszej osoby.

Reguła Naismitha pojawia się w brytyjskim prawie stanowionym, chociaż nie z nazwy. Zasady licencjonowania działalności przygodowej mają zastosowanie do dostawców różnych atrakcji, w tym trekkingu. Częścią definicji trekkingu jest to, że jest to teren, po którym dotarcie do drogi lub schroniska (najszybszą bezpieczną trasą) zajęłoby ponad 30 minut, w oparciu o prędkość marszu 5 kilometrów na godzinę plus dodatkowa minuta na co 10 metrów podjazdu.

Wykres zależności prędkości chodu od nachylenia , wynikający z reguły Naismitha i poprawek Langmuira dla prędkości bazowych 5 km/h i 4 km/h w porównaniu z funkcją wędrówki Toblera .

Równoważność szalika między odległością a wznoszeniem

Alternatywnie, regułę można wykorzystać do określenia równoważnej płaskiej odległości trasy. Osiąga się to poprzez uznanie, że reguła Naismitha implikuje równoważność odległości i wznoszenia pod względem czasu: 3 mile (= 15 840 stóp) odległości jest równoważne pod względem czasu 2000 stóp wznoszenia.

Profesor Philip Scarf, prodziekan ds. badań i innowacji oraz profesor statystyki stosowanej na Uniwersytecie w Salford , w badaniach opublikowanych w 2008 r. podaje następującą formułę:

odległość równoważna = x + α·y

Gdzie:

x = odległość w poziomie

y = odległość w pionie

α = 7,92 (3 mil / 2000 stóp), zwana przez Scarfa liczbą Naismitha

Oznacza to, że 7,92 jednostek odległości odpowiada 1 jednostce wznoszenia. Dla wygody można zastosować regułę 8 do 1. Na przykład, jeśli trasa ma 20 kilometrów (12 mil) i 1600 metrów przewyższenia (jak w przypadku pierwszego etapu rundy Boba Grahama , Keswick do Threlkeld), równoważna płaska odległość tej trasy wynosi 20+(1,6×8)=32,8 km (20,4 mil). Zakładając, że osoba może utrzymać prędkość na płaskim terenie 5 km/h, trasa zajmie 6 godzin i 34 minuty. Prostota tego podejścia polega na tym, że potrzebny czas można łatwo dostosować do własnej (wybranej) prędkości danej osoby na płaskim terenie; przy 8 km/h (płaska prędkość) trasa zajmie 4 godziny i 6 minut. Reguła została przetestowana na spadających czasach działania i okazała się niezawodna. Szalik zaproponował tę równoważność w 1998 roku.

Jak widać, założenie szalika pozwala również na obliczenie czasu dla każdej prędkości, a nie tylko jednej, jak w przypadku oryginalnej reguły Naismitha.

Tempo

Tempo jest odwrotnością prędkości. Można to obliczyć tutaj z następującego wzoru:

p = p0·(1 + α·m)

Gdzie:

p = tempo

p0 = tempo na płaskim terenie

m = nachylenie pod górę

Ten wzór jest prawdziwy dla m≥0 (teren pod górę lub płaski). Zakłada równoważność odległości i wznoszenia poprzez zastosowanie wspomnianego wcześniej współczynnika α.

Przykładowe obliczenia: p0 = 12 min/km (dla prędkości 5 km/h), m = 0,6 km wznoszenia / 5 km dystansu = 0,12, p = 12 · (1 + 7,92 · 0,12) = 23,4 min/km.

Inne modyfikacje

Na przestrzeni lat sformułowano kilka poprawek, starając się uczynić regułę dokładniejszą, uwzględniając dalsze zmienne, takie jak przewożony ładunek, nierówność terenu, zjazdy i sprawność (lub jej brak). Dokładność niektórych poprawek jest kwestionowana, w szczególności prędkość, z jaką spacerowicze schodzą po łagodnym nachyleniu . Żadna prosta formuła nie jest w stanie objąć pełnej różnorodności warunków górskich i indywidualnych możliwości.

Korekty Trantera

Korekty Trantera uwzględniają kondycję i zmęczenie. Sprawność fizyczna jest określana na podstawie czasu potrzebnego do pokonania 1000 stóp na dystansie ½ mili (800 m). Dodatkowe korekty dla nierównego lub niestabilnego terenu lub warunków można oszacować, obniżając jeden lub więcej poziomów sprawności.

Indywidualna sprawność fizyczna w kilka minut	Czas w godzinach oszacowany przy użyciu reguły Naismitha
Indywidualna sprawność fizyczna w kilka minut	2	3	4	5	6	7	8	9	10	12	14	16	18	20	22	24
15 (bardzo pasuje)	1	1.5	2	2,75	3.5	4.5	5.5	6,75	7,75	10	12,5	14,5	17	19,5	22	24
20	1,25	2.25	3.25	4.5	5.5	6.5	7,75	8.75	10	12,5	15	17,5	20	23
25	1.5	3	4.25	5.5	7	8.5	10	11,5	13.25	15	17,5
30	2	3.5	5	6,75	8.5	10,5	12,5	14,5
40	2,75	4.25	5,75	7,5	9.5	11,5			Zbyt wiele, aby spróbować
50 (niezdolny)	3.25	4,75	6.5	8.5

Na przykład, jeśli reguła Naismitha szacuje czas podróży na 9 godzin, a Twój poziom sprawności wynosi 25, powinieneś przeznaczyć na to 11,5 godziny.

Korekty Aitkena

Aitken (1977) zakłada, że 1 godzina zajmuje pokonanie 3 mil (5 km) na ścieżkach, torach i drogach, podczas gdy na wszystkich innych powierzchniach czas ten zmniejsza się do 2½ mil (4 km).

Dla obu dystansów daje dodatkową 1 godzinę na 2000 stóp (600 m) wznoszenia. Tak więc Aitken nie bierze pod uwagę równoważności między odległością a wzniesieniem (zaproponowane przez Scarfa w 1998 r.).

poprawki Langmuira

Langmuir (1984) rozszerza regułę pochodzenia. Zakłada on, że Naismitha wynosi 5 km/h i wprowadza następujące dalsze udoskonalenia dotyczące zjeżdżania ze wzniesienia:

Dla łagodnego spadku (zbocza od 5 stopni do 12 stopni) odejmij 10 minut na każde 300 metrów zejścia
W przypadku stromego spadku (zbocza większe niż 12 stopni) dodaj 10 minut na każde 300 metrów zejścia

Później mówi, że należy wziąć pod uwagę sprawność najwolniejszego członka drużyny, dlatego bardziej praktyczną formułą dla grupy jest:

4 km/h + 1 h / 450 m podbiegu

Zobacz też

Notatki

Linki zewnętrzne