Numer Strahlera

Diagram przedstawiający kolejność strumienia Strahlera

W matematyce liczba Strahlera lub liczba Hortona-Strahlera drzewa matematycznego jest numeryczną miarą jego złożoności rozgałęzień.

Liczby te zostały po raz pierwszy opracowane w hydrologii przez Roberta E. Hortona ( 1945 ) i Arthura Newella Strahlera ( 1952 , 1957 ); w tej aplikacji są one określane jako porządek strumienia Strahlera i służą do definiowania rozmiaru strumienia na podstawie hierarchii dopływów . Powstają one również w analizie systemów L i hierarchicznych struktur biologicznych, takich jak drzewa (biologiczne) oraz układy oddechowe i krążeniowe zwierząt, w przydzielaniu rejestrów dla kompilacji języków programowania wysokiego poziomu oraz w analizie sieci społecznościowych . Alternatywne systemy porządkowania strumieni zostały opracowane przez Shreve i Hodgkinson et al. Statystyczne porównanie systemów Strahler i Shreve wraz z analizą długości strumieni/łączy podaje Smart.

Definicja

Wszystkie drzewa w tym kontekście są grafami skierowanymi , zorientowanymi od korzenia w kierunku liści; innymi słowy, są drzewami . Stopień węzła w drzewie to po prostu liczba jego dzieci. Można przypisać numer Strahlera do wszystkich węzłów drzewa, w kolejności od dołu do góry, w następujący sposób:

• Jeśli węzeł jest liściem (nie ma dzieci), jego liczba Strahlera wynosi jeden.
• Jeśli węzeł ma jedno dziecko o numerze Strahlera i , a wszystkie inne dzieci mają numery Strahlera mniejsze niż i , to ponownie numerem Strahlera węzła jest i .
• Jeśli węzeł ma dwoje lub więcej dzieci o liczbie Strahlera i i nie ma dzieci o większej liczbie, to liczba Strahlera węzła wynosi i + 1.

Liczba Strahlera drzewa to numer jego węzła głównego.

Algorytmicznie numery te można przypisać, wykonując przeszukiwanie w głąb i przypisując każdemu węzłowi numer w postorder . Te same liczby można również wygenerować w procesie przycinania, w którym drzewo jest upraszczane w sekwencji etapów, gdzie na każdym etapie usuwa się wszystkie węzły liści i wszystkie ścieżki węzłów pierwszego stopnia prowadzące do liści: liczba Strahlera węzeł to etap, na którym zostałby usunięty przez ten proces, a liczba Strahlera drzewa to liczba etapów wymaganych do usunięcia wszystkich jego węzłów. Inną równoważną definicją liczby Strahlera drzewa jest to, że jest to wysokość największego kompletne drzewo binarne , które można homeomorficznie osadzić w danym drzewie; liczba Strahlera węzła w drzewie jest podobnie wysokością największego kompletnego drzewa binarnego, które można osadzić poniżej tego węzła.

  Każdy węzeł o liczbie Strahlera i musi mieć co najmniej dwóch potomków o liczbie Strahlera i - 1, co najmniej czterech potomków o liczbie Strahlera i - 2 itd. oraz co najmniej 2 ^{i - 1} potomków liścia. Dlatego w drzewie z n węzłami największa możliwa liczba Strahlera to log ₂ n + 1. Jednak jeśli drzewo nie tworzy pełnego drzewa binarnego, jego liczba Strahlera będzie mniejsza niż ta granica. W n -węzłowym drzewie binarnym wybrano   równomiernie losowo spośród wszystkich możliwych drzew binarnych , oczekiwany indeks pierwiastka jest z dużym prawdopodobieństwem bardzo bliski log ₄ n .

Aplikacje

Sieci rzeczne

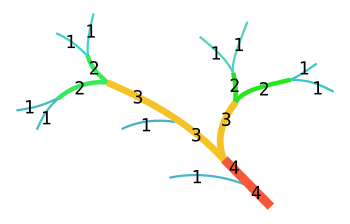
W zastosowaniu kolejności strumieni Strahlera do hydrologii każdy odcinek strumienia lub rzeki w sieci rzecznej jest traktowany jako węzeł w drzewie, a następny odcinek poniżej jest jego rodzicem. Kiedy dwa pierwszego rzędu spotykają się, tworzą strumień drugiego rzędu . Kiedy dwa strumienie drugiego rzędu spotykają się, tworzą trzeciego rzędu . Strumienie niższego rzędu łączące się ze strumieniem wyższego rzędu nie zmieniają kolejności strumienia wyższego rzędu. Tak więc, jeśli strumień pierwszego rzędu łączy się ze strumieniem drugiego rzędu, pozostaje strumieniem drugiego rzędu. Dopiero gdy strumień drugiego rzędu połączy się z innym strumieniem drugiego rzędu, staje się strumieniem trzeciego rzędu. Podobnie jak w przypadku drzew matematycznych, segment z indeksem i musi być zasilany przez co najmniej 2 ^{i - 1} różnych dopływów o indeksie 1. Shreve zauważył, że praw Hortona i Strahlera należy oczekiwać od dowolnego topologicznie losowego rozkładu. Późniejszy przegląd relacji potwierdził ten argument, stwierdzając, że z właściwości opisanych przez prawa nie można wyciągnąć żadnych wniosków wyjaśniających strukturę lub pochodzenie sieci strumieni.

Aby zakwalifikować się jako strumień, cecha hydrologiczna musi być albo powtarzalna, albo wieloletnia . Powtarzające się (lub „przerywane”) strumienie mają wodę w kanale przez co najmniej część roku. Indeks strumienia lub rzeki może wahać się od 1 (strumień bez dopływów) do 12 (najpotężniejsza rzeka na świecie, Amazonka , u ujścia). Rzeka Ohio jest rzędu ósmego, a Mississippi rzędu 10. Szacuje się, że 80% strumieni na planecie to strumienie górnego rzędu od pierwszego do trzeciego rzędu .

Jeśli współczynnik bifurkacji sieci rzecznej jest wysoki, istnieje większe prawdopodobieństwo powodzi. Byłby też niższy czas koncentracji. Współczynnik rozwidlenia może również pokazać, które części zlewni są bardziej narażone na powodzie, porównując, patrząc na oddzielne wskaźniki. Większość brytyjskich rzek ma współczynnik bifurkacji między 3 a 5.

Porównanie nieprawidłowej i prawidłowej konwersji zbiorników wodnych na sieć drzew

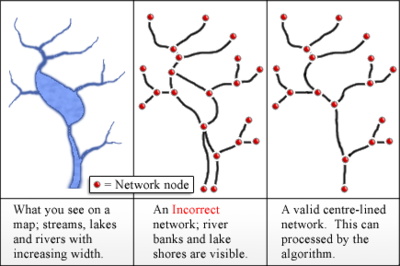
Gleyzer i in. (2004) opisują sposób obliczania wartości kolejności strumienia Strahlera w aplikacji GIS . Algorytm ten jest realizowany przez RivEX , narzędzie ESRI ArcGIS 10.7. Dane wejściowe do ich algorytmu to sieć linii środkowych zbiorników wodnych, reprezentowana jako łuki (lub krawędzie) połączone w węzłach. Granice jezior i brzegi rzek nie powinny być używane jako łuki, ponieważ będą one generalnie tworzyć sieć inną niż drzewo o nieprawidłowej topologii.

Inne systemy hierarchiczne

Numerację Strahlera można zastosować w analizie statystycznej dowolnego systemu hierarchicznego, nie tylko do rzek.

• Arenas i in. (2004) opisują zastosowanie indeksu Hortona-Strahlera w analizie sieci społecznościowych .
• Ehrenfeucht, Rozenberg i Vermeir (1981) zastosowali wariant numeracji Strahlera (zaczynając od zera na liściach zamiast jedynki), który nazwali rangą drzewa , do analizy systemów L.
• Numeracja Strahlera została również zastosowana do hierarchii biologicznych, takich jak rozgałęzione struktury drzew oraz układy oddechowe i krążenia zwierząt.

Zarejestruj alokację

Podczas tłumaczenia języka programowania wysokiego poziomu na język asemblera minimalna liczba rejestrów wymagana do oceny drzewa wyrażeń jest dokładnie jego liczbą Strahlera. W tym kontekście numer Strahlera można również nazwać numerem rejestru .

W przypadku drzew wyrażeń, które wymagają większej liczby rejestrów niż jest dostępnych, algorytm Sethi-Ullmana może być użyty do przetłumaczenia drzewa wyrażeń na sekwencję instrukcji maszynowych, które wykorzystują rejestry tak wydajnie, jak to możliwe, minimalizując liczbę przypadków rozlania wartości pośrednich z rejestrów do pamięci głównej i całkowitą liczbę instrukcji w wynikowym skompilowanym kodzie.

Powiązane parametry

Stosunek bifurkacji

Z liczbami Strahlera drzewa powiązane są współczynniki bifurkacji , liczby opisujące, jak bliskie jest zrównoważeniu drzewo. Dla każdego rzędu i w hierarchii i -ty współczynnik bifurkacji wynosi

${\ Displaystyle {\ Frac {n_ {i}} {n_ {i + 1}}}}$

gdzie n _i oznacza liczbę węzłów o kolejności i .

Współczynnik bifurkacji całej hierarchii można obliczyć, uśredniając współczynniki bifurkacji w różnych rzędach. W pełnym drzewie binarnym współczynnik bifurkacji będzie wynosił 2, podczas gdy inne drzewa będą miały większe współczynniki bifurkacji. Jest to liczba bezwymiarowa.

Szerokość ścieżki

Szerokość ścieżki dowolnego nieskierowanego grafu G można zdefiniować jako najmniejszą liczbę w taką, że istnieje graf interwałowy H zawierający G jako podgraf, z największą kliką w H mającą w + 1 wierzchołki. W przypadku drzew (postrzeganych jako grafy nieskierowane przez zapomnienie o ich orientacji i korzeniu) szerokość ścieżki różni się od liczby Strahlera, ale jest z nią ściśle związana: w drzewie o szerokości ścieżki w i liczbie Strahlera s , te dwie liczby są powiązane nierównościami

w ≤ s ≤ 2 w + 2.

Zdolność do obsługi wykresów z cyklami, a nie tylko drzewami, daje pathwidth dodatkową wszechstronność w porównaniu z liczbą Strahlera. Jednak w przeciwieństwie do liczby Strahlera, szerokość ścieżki jest zdefiniowana tylko dla całego grafu, a nie osobno dla każdego węzła w grafie.

Zobacz też

• Główny rdzeń rzeki, zwykle znajdowany wzdłuż odnogi o najwyższym numerze Strahlera
• System kodowania Pfafstetter

Notatki

•   Arenas, A.; Danon, L.; Díaz-Guilera, A.; Gleiser, PM; Guimerá, R. (2004), „Analiza społeczności w sieciach społecznościowych”, European Physical Journal B , 38 (2): 373–380, arXiv : cond-mat/0312040 , Bibcode : 2004 EPJB...38..373A , doi : 10.1140/epjb/e2004-00130-1 , S2CID 9764926 .
•    Borchert, Rolf; Slade, Norman A. (1981), „Współczynniki rozwidlenia i adaptacyjna geometria drzew”, Botanical Gazette , 142 (3): 394–401, doi : 10,1086/337238 , hdl : 1808/9253 , JSTOR 2474363 , S2CID 84145477 .
• Devroye, Luc ; Kruszewski, Paul (1995), „Uwaga na temat liczby Hortona-Strahlera dla przypadkowych drzew”, Information Processing Letters , 56 (2): 95–99, doi : 10.1016/0020-0190 (95) 00114-R .
•   Devroye, L .; Kruszewski, P. (1996), „O liczbie Hortona-Strahlera dla losowych prób” , RAIRO Informatique Théorique et Applications , 30 (5): 443–456, doi : 10.1051/ita/1996300504431 , MR 1435732
•   Ehrenfeucht, A .; Rozenberg, G .; Vermeir, D. (1981), „O systemach ETOL o skończonej randze drzewa”, SIAM Journal on Computing , 10 (1): 40–58, doi : 10.1137/0210004 , MR 0605602 .
•   Ershov, AP (1958), „O programowaniu operacji arytmetycznych”, Komunikaty ACM , 1 (8): 3–6, doi : 10.1145 / 368892.368907 , S2CID 15986378 .
• Flajolet, P .; Raoult, JC; Vuillemin, J. (1979), „Liczba rejestrów wymaganych do oceny wyrażeń arytmetycznych”, Theoretical Computer Science , 9 (1): 99–125, doi : 10.1016/0304-3975 (79) 90009-4 .
•   Gleyzer, A.; Denisyuk, M.; Rimmer, A.; Salingar, Y. (2004), „Szybki rekurencyjny algorytm GIS do obliczania kolejności strumienia Strahlera w sieciach plecionych i nieplecionych”, Journal of the American Water Resources Association , 40 (4): 937–946, Bibcode : 2004JAWRA..40. .937G , doi : 10.1111/j.1752-1688.2004.tb01057.x , S2CID 128399321 .
•    Horsfield, Keith (1976), „Niektóre właściwości matematyczne rozgałęzień drzew z zastosowaniem do układu oddechowego”, Bulletin of Mathematical Biology , 38 (3): 305–315, doi : 10.1007 / BF02459562 , PMID 1268383 , S2CID 189888885 .
•   Horton, RE (1945), „Rozwój erozyjny strumieni i ich zlewni: hydrofizyczne podejście do morfologii ilościowej” , Geological Society of America Bulletin , 56 (3): 275–370, doi : 10.1130 / 0016-7606 (1945 )56[275:EDOSAT]2.0.CO;2 , S2CID 129509551 .
• Lanfear, KJ (1990), „Szybki algorytm do automatycznego obliczania kolejności strumienia Strahlera”, Journal of the American Water Resources Association , 26 (6): 977–981, Bibcode : 1990JAWRA..26..977L , doi : 10.1111/ j.1752-1688.1990.tb01432.x .
• Luttenberger, Michael; Schlund, Maxmilian (2011), Rozszerzenie twierdzenia Parikha poza idempotencję , arXiv : 1112,2864 , Bibcode : 2011arXiv1112,2864L
• Strahler, AN (1952), „Analiza hipsometryczna (obszar-wysokość) topologii erozyjnej”, Geological Society of America Bulletin , 63 (11): 1117–1142, doi : 10.1130/0016-7606 (1952) 63 [1117: HAAOET ]2.0.CO;2 .
• Strahler, AN (1957), „Analiza ilościowa geomorfologii zlewni”, Transactions of the American Geophysical Union , 38 (6): 913–920, Bibcode : 1957TrAGU..38..913S , doi : 10.1029/tr038i006p00913 .
• Waugh, David (2002), Geografia, zintegrowane podejście (wyd. 3), Nelson Thornes .