Słabo łańcuchowa macierz dominująca po przekątnej

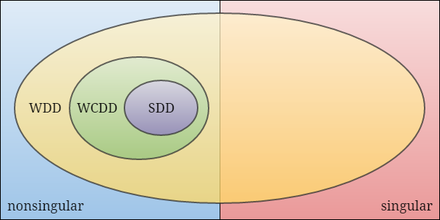
Diagram Venna przedstawiający zawieranie słabo łańcuchowych macierzy dominujących diagonalnie (WCDD) w stosunku do macierzy słabo dominujących diagonalnie (WDD) i ściśle dominujących diagonalnie (SDD).

W matematyce słabo łańcuchowe macierze dominujące po przekątnej to rodzina macierzy nieosobliwych , która obejmuje macierze ściśle dominujące po przekątnej .

Definicja

Czynności wstępne

Mówimy $jest$$macierzy$ złożonej ${\ Displaystyle | a_ {ii} |> \ textstyle {\ suma _ {j \ neq i}} | a_ {ij} |}$ SDD ) jeśli . Mówimy, $SDD,$ jeśli wszystkie jego wiersze to SDD. Słabo przekątna dominująca (WDD) jest definiowana za pomocą ${\ displaystyle \ geq}$ .

Skierowany wykres związany z $\$ zespoloną $Displaystyle A = (a_ {ij})}$ dany przez wierzchołki ${\ Displaystyle \ {1, \ ldots, m \}}$ i krawędzie zdefiniowane w następujący sposób: istnieje krawędź od ${\ Displaystyle i \ rightarrow j}$ wtedy i tylko wtedy, gdy ${\ Displaystyle a_ {ij} \ neq 0}$ .

Definicja

, że złożona macierz kwadratowa jest słabo ukośna dominująca po przekątnej (WCDD), jeśli ZA $\ displaystyle A}$

• ${\ displaystyle A}$ jest WDD i
• dla każdego wiersza $cdots \ strzałka w prawo i_ {k}}$$→$ ja k { \ na skierowanym wykresie kończącym się na rzędzie SDD $ja$$displaystyle i_ {k}}$ .

Przykład

Wykres skierowany powiązany z macierzą WCDD w przykładzie. Pierwszy wiersz, który jest SDD, jest podświetlony. Zauważ, że niezależnie od tego, od którego węzła $zaczniemy$ , możemy znaleźć spacer $\ Displaystyle i \ rightarrow (i-1) \ rightarrow (i-2)\rightarrow \cdots \rightarrow 1}$ .

Macierz $\ razy m}$ m

${\ Displaystyle {\ rozpocząć {pmatrix} 1 \\ - 1 i 1 \\& - 1 i 1 \\&& \ ddots & \ ddots \\&&& -1 i 1 \ koniec {pmatrix }}}$

jest WCDD.

Nieruchomości

Nieosobliwość

Macierz WCDD nie jest liczbą pojedynczą.

Dowód : Niech $Displaystyle A = (a_ {ij})}$ będzie macierzą WCDD. Załóżmy, że istnieje niezerowa wartość $displaystyle$ przestrzeni zerowej $A}$ . Bez utraty ogólności niech $,$ takie ${\ Displaystyle | x_ {i_ {1}} | = 1 \ geq | x_ {j} |}$ dla wszystkich ${\ displaystyle j}$ . Ponieważ ZA $\ Displaystyle A}$ to WCDD, możemy wybrać spacer kończący się ${\ Displaystyle i_ {1} \ rightarrow i_ {2} \ rightarrow \ cdots \ rightarrow i_ {k}}$ w rzędzie SDD ${\ displaystyle i_ {k}}$ .

Biorąc moduły po obu stronach

$\ Displaystyle -a_ {i_ {1}i_ {1}} x_ {i_ {1}} = \ suma _ {j \ neq i_{1}}a_{i_{1}j}x_{j}}$

i zastosowanie nierówności trójkąta daje plony

${\ Displaystyle \ lewo | a_ {i_ {1} i_ {1}} \ prawo | \ równoważnik \ suma _ {j \ neq i_ {1}} \ lewo | a_ {i_ {1} j} \ prawo |\ left|x_{j}\right|\leq \sum _{j\neq i_{1}}\left|a_{i_{1}j}\right|,}$

a zatem wiersz nie jest SDD. ${\ displaystyle i_ {1}}$ Ponadto, ponieważ jest to $że$ , powyższy łańcuch nierówności zachodzi z równością, tak ${\ Displaystyle | x_ {j} | = 1} ilekroć$${\ Displaystyle a_ {i_ {1} j} \ neq 0$ jot . Dlatego ${\ Displaystyle | x_ {i_ {2}} | = 1}$ . Powtarzając ten argument z ${\ displaystyle i_ {2}}$ , ${\ displaystyle i_ {3}}$ itd. stwierdzamy, że ${\ displaystyle i_ {k}}$ nie jest SDD, co jest sprzecznością. ${\ Displaystyle \ kwadrat}$

Pamiętając, że macierz nieredukowalna to taka, której skojarzony graf skierowany jest silnie spójny , trywialnym następstwem powyższego jest to, że macierz nieredukowalnie dominująca diagonalnie (tj. nieredukowalna macierz WDD z co najmniej jednym wierszem SDD) jest nieosobliwa.

Związek z nieosobliwymi M-macierzami

Następujące są równoważne:

• ${\ displaystyle A}$ jest nieosobliwą macierzą WDD M. ZA {\ displaystyle A }
• $nieosobliwą$ WDD L ;
• jest macierzą L WCDD ; ${\ displaystyle A}$

W rzeczywistości macierze L WCDD były badane (przez Jamesa H. Bramble'a i BE Hubbarda) już w 1964 roku w artykule w czasopiśmie, w którym pojawiają się pod alternatywną nazwą macierzy typu pozytywnego .

Ponadto, jeśli jest $WCDD$ , możemy powiązać jej odwrotność w następujący sposób: ZA ${\ displaystyle n \ razy n}$

$\ Displaystyle \ lewo \ Vert A ^ {- 1} \ prawo \ Vert _ {\ infty} \ leq \sum _{i}\left[a_{ii}\prod _{j=1}^{i}(1-u_{j})\right]^{-1}}$ gdzie ${\ Displaystyle u_ {i} = {\ Frac {1} {\ lewo | a_ {ii} \ prawo |}} \ suma _ {j = i + 1} ^ {n} \ lewo | a_ {ij} \ prawo |.}$

Zauważ, że $u$ zero, a prawa strona powyższego ograniczenia wynosi ${\ displaystyle \ infty}$ , ilekroć jedna lub więcej stałych jest $\ displaystyle u_ {i} }$ jest jeden.

Znane są ściślejsze granice odwrotności macierzy L WCDD.

Aplikacje

Ze względu na ich związek z macierzami M (patrz wyżej ), macierze WCDD często pojawiają się w praktycznych zastosowaniach. Poniżej podano przykład.

Monotoniczne schematy numeryczne

L-macierze WCDD powstają naturalnie ze schematów aproksymacji monotonicznej dla równań różniczkowych cząstkowych .

Rozważmy na przykład jednowymiarowy problem Poissona

${\ Displaystyle u ^ {\ pierwsza \ pierwsza} (x) + g (x) = 0}$ dla ${\ Displaystyle x \ w (0, 1)}$

z warunkami brzegowymi Dirichleta ${\ Displaystyle u (0) = u (1) = 0}$ . Pozwalając $,$ siatką numeryczną (dla pewnego $,$ jedność schemat monotonicznych różnic skończonych dla problemu Poissona ma postać

${\ Displaystyle - {\ Frac {1} {h ^ {2}}} A {\ vec {u}} + {\ vec {g}} = 0}$ gdzie ${\ Displaystyle [{\ vec {g}}] _ {j} = g (jh)}$

I

${\ Displaystyle A = {\ rozpocząć {pmatrix} 2&-1 \\-1&2&-1\\&-1&2&-1\\&&\ddots &\ddots &\ddots \\&&&-1&2&-1\\&&&&-1&2 \end{pmacierz}}.}$

Zauważ, że jest $.$ -macierzą WCDD