Skala (mapa)

Skala graficzna lub słupkowa. Mapa zwykle podawałaby również swoją skalę liczbowo (na przykład „1:50 000” oznacza, że jeden cm na mapie reprezentuje 50 000 cm rzeczywistej przestrzeni, czyli 500 metrów)

Skala słupkowa ze skalą nominalną wyrażoną zarówno jako „1 cm = 6 km”, jak i „1:600 000” (odpowiednik, bo 6 km = 600 000 cm)

Skala mapy to stosunek odległości na mapie do odpowiadającej jej odległości w terenie . Ta prosta koncepcja jest skomplikowana przez krzywiznę powierzchni Ziemi , która wymusza zmianę skali na mapie. Z powodu tej zmienności pojęcie skali nabiera znaczenia na dwa różne sposoby.

Pierwszym sposobem jest stosunek wielkości globu generującego do wielkości Ziemi. Generujący globus jest konceptualnym modelem, do którego skurczyła się Ziemia iz którego rzutowana jest mapa . Stosunek wielkości Ziemi do wielkości globu generującego nazywa się skalą nominalną (= skala główna = ułamek reprezentatywny ). Wiele map podaje skalę nominalną, a nawet może wyświetlać skalę słupkową (czasami nazywaną po prostu „skalą”), aby ją przedstawić.

Druga odrębna koncepcja skali odnosi się do zmienności skali na mapie. Jest to stosunek skali odwzorowanego punktu do skali nominalnej. W tym przypadku „skala” oznacza współczynnik skali (= skala punktowa = określona skala ).

Jeśli region mapy jest wystarczająco mały, aby zignorować krzywiznę Ziemi, na przykład na planie miasta, wówczas pojedyncza wartość może być używana jako skala bez powodowania błędów pomiaru. Na mapach obejmujących większe obszary lub całą Ziemię skala mapy może być mniej przydatna lub wręcz bezużyteczna w pomiarze odległości. Odwzorowanie mapy staje się kluczowe dla zrozumienia, jak zmienia się skala na mapie. Gdy skala zmienia się zauważalnie, można to uwzględnić jako współczynnik skali. Wskaźnik Tissota jest często używany do zilustrowania zmienności skali punktowej na mapie.

Historia

Podstawy ilościowego skalowania map sięgają starożytnych Chin z tekstowymi dowodami, że idea skalowania map była rozumiana już w II wieku pne. Starożytni chińscy geodeci i kartografowie dysponowali wystarczającymi zasobami technicznymi używanymi do tworzenia map, takimi jak pręty liczące , kątowniki stolarskie , piony , kompasy do rysowania kół i rurek celowniczych do pomiaru nachylenia. Układy odniesienia postulujące rodzący się układ współrzędnych do identyfikacji lokalizacji zostały zasugerowane przez starożytnych chińskich astronomów, którzy podzielili niebo na różne sektory lub loże księżycowe.

Chiński kartograf i geograf Pei Xiu z okresu Trzech Królestw stworzył zestaw wielkopowierzchniowych map narysowanych w skali. Stworzył zestaw zasad, które podkreślały znaczenie spójnego skalowania, pomiarów kierunkowych i korekt pomiarów terenu w terenie, który był mapowany.

Terminologia

Reprezentacja skali

Skale mapy mogą być wyrażone słownie (skala leksykalna), jako stosunek lub jako ułamek. Przykładami są:

„jeden centymetr do stu metrów” lub 1:10 000 lub 1/10 000

„jeden cal do jednej mili” lub 1:63 360 lub 1/63 360

„jeden centymetr do tysiąca kilometrów” lub 1:100 000 000 lub 1/100 000 000. (Stosunek byłby zwykle skracany do 1:100M)

Skala słupkowa a skala leksykalna

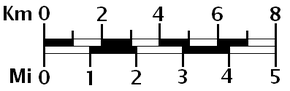
Oprócz powyższego wiele map zawiera jedną lub więcej (graficznych) podziałek słupkowych . Na przykład niektóre współczesne mapy brytyjskie mają trzy skale słupkowe, po jednej dla kilometrów, mil i mil morskich.

Skala leksykalna w języku znanym użytkownikowi może być łatwiejsza do zobrazowania niż stosunek: jeśli skala wynosi od cala do dwóch mil , a użytkownik mapy widzi na mapie dwie wioski oddalone od siebie o około dwa cale, to łatwo aby dowiedzieć się, że wioski są oddalone od siebie o około cztery mile.

Skala leksykalna może powodować problemy, jeśli jest wyrażona w języku, którego użytkownik nie rozumie lub w przestarzałych lub źle zdefiniowanych jednostkach. Na przykład skala od jednego cala do furlonga (1:7920) będzie zrozumiała dla wielu starszych osób w krajach, w których jednostki imperialne były kiedyś nauczane w szkołach. Ale skala jednego puszy do jednej ligi może wynosić około 1:144 000, w zależności od wyboru przez kartografa spośród wielu możliwych definicji ligi, a tylko mniejszość współczesnych użytkowników będzie zaznajomiona z używanymi jednostkami.

Duża skala, średnia skala, mała skala

Kontrast do skali przestrzennej .

Mapa jest klasyfikowana jako mała lub duża , a czasami średnia . Mała skala odnosi się do map świata lub map dużych regionów, takich jak kontynenty lub duże narody. Innymi słowy, pokazują duże obszary ziemi na małej przestrzeni. Nazywa się je małą skalą, ponieważ reprezentatywna frakcja jest stosunkowo niewielka.

Mapy w dużej skali przedstawiają bardziej szczegółowo mniejsze obszary, na przykład mapy hrabstw lub plany miast. Takie mapy nazywane są wielkoskalowymi, ponieważ reprezentatywny ułamek jest stosunkowo duży. Na przykład plan miasta, który jest mapą w dużej skali, może mieć skalę 1:10 000, podczas gdy mapa świata, która jest mapą w małej skali, może mieć skalę 1:100 000 000.

Poniższa tabela opisuje typowe zakresy dla tych skal, ale nie należy jej uważać za miarodajną, ponieważ nie ma standardu:

Klasyfikacja	Zakres	Przykłady
duża skala	1:0 – 1:600 000	1:0.00001 dla mapy wirusa; 1:5000 dla mapy spacerowej miasta
średnia skala	1:600 000 – 1:2 000 000	Mapa kraju
mała skala	1:2 000 000 – 1:∞	1:50 000 000 dla mapy świata; 1:10 ²¹ dla mapy galaktyki

Terminy są czasami używane w znaczeniu bezwzględnym tabeli, ale innym razem w znaczeniu względnym. Na przykład czytelnik map, którego praca odnosi się wyłącznie do map w dużej skali (jak w powyższej tabeli), może odnosić się do mapy w skali 1: 500 000 jako małej skali.

W języku angielskim słowo duża skala jest często używane w znaczeniu „rozległy”. Jednak, jak wyjaśniono powyżej, kartografowie używają terminu „duża skala” w odniesieniu do mniej obszernych map – takich, które pokazują mniejszy obszar. Mapy przedstawiające rozległy obszar to mapy „małej skali”. Może to być przyczyną zamieszania.

Zmienność skali

Mapowanie dużych obszarów powoduje zauważalne zniekształcenia, ponieważ znacznie spłaszcza zakrzywioną powierzchnię ziemi. Sposób dystrybucji zniekształceń zależy od odwzorowania mapy . Skala zmienia się w zależności od mapy , a podana skala mapy jest tylko przybliżeniem. Zostało to szczegółowo omówione poniżej.

Mapy wielkoskalowe z pominięciem krzywizny

Region, w którym ziemię można uznać za płaską, zależy od dokładności pomiarów geodezyjnych . Jeśli mierzona jest tylko z dokładnością do jednego metra, to krzywizna Ziemi jest niewykrywalna na długości południka około 100 kilometrów (62 mil) i na linii wschód-zachód na długości około 80 km (na 45 stopniach szerokości geograficznej ). Przy pomiarze z dokładnością do 1 milimetra (0,039 cala) krzywizna jest niewykrywalna na odcinku południka wynoszącym około 10 km i na linii wschód-zachód wynoszącej około 8 km. Stąd plan Nowego Jorku z dokładnością do jednego metra lub plan placu budowy z dokładnością do jednego milimetra spełniałyby powyższe warunki pominięcia krzywizny. Można je traktować za pomocą pomiarów płaskich i mapować za pomocą rysunków w skali, na których dowolne dwa punkty w tej samej odległości na rysunku znajdują się w tej samej odległości na ziemi. Rzeczywiste odległości terenowe oblicza się, mierząc odległość na mapie, a następnie mnożąc ją przez odwrotność ułamka skali lub, równoważnie, po prostu używając dzielników, aby przenieść odległość między punktami na mapie na skalę słupkową na mapie.

Skala punktowa (lub określona skala)

Jak dowodzi twierdzenie Gaussa Egregium , kuli (lub elipsoidy) nie można rzutować na płaszczyznę bez zniekształceń. Powszechnie ilustruje to niemożność wygładzenia skórki pomarańczy na płaskiej powierzchni bez jej rozerwania i zdeformowania. Jedyną prawdziwą reprezentacją kuli w stałej skali jest inna kula, taka jak kula ziemska .

Biorąc pod uwagę ograniczony praktyczny rozmiar globusów, musimy używać map do szczegółowego mapowania. Mapy wymagają projekcji. Projekcja implikuje zniekształcenie: stała separacja na mapie nie odpowiada stałej separacji na ziemi. Chociaż mapa może wyświetlać graficzną skalę słupkową, należy używać skali ze świadomością, że będzie ona dokładna tylko na niektórych liniach mapy. (Jest to omówione dalej w przykładach w poniższych sekcjach).

Niech P $będzie$ punktem na szerokości $geograficznej$ długości na kuli (lub elipsoidzie ) Niech Q będzie sąsiednim punktem i niech będzie kątem między elementem PQ a południkiem w P: ten kąt jest $kątem$ azymutu PQ. Niech P' i Q' będą odpowiednimi punktami rzutu. Kąt między kierunkiem P'Q' a rzutem południka to namiar ${\ displaystyle \ beta}$ . Ogólnie ${\ Displaystyle \ alpha \ neq \ beta}$ . Komentarz: to dokładne rozróżnienie między azymutem (na powierzchni Ziemi) a namiarem (na mapie) nie jest powszechnie przestrzegane, wielu pisarzy używa tych terminów prawie zamiennie.

Definicja: skala punktowa w P jest stosunkiem dwóch odległości P'Q' i PQ w granicy, do której Q zbliża się do P. Zapisujemy to jako

{\ Displaystyle \ mu (\ lambda, \, \ varphi, \, \ alfa) = \ _ _ {Q \ do P}} \frac {P'Q'}{PQ}},}

gdzie zapis wskazuje, że skala punktowa jest funkcją położenia P, a także kierunku elementu PQ.

Definicja: $(\ lambda, \, \ varphi )}$ P i Q leżą na tym samym południku $) {$ południka jest oznaczona przez .

Definicja: jeśli P i Q leżą $lambda ,\,\varphi )}$ tej samej równoległości $) {$ jest oznaczona przez $k$ .

Definicja: jeśli skala punktowa zależy tylko od położenia, a nie od kierunku, mówimy, że jest izotropowa i konwencjonalnie oznaczamy jej wartość w dowolnym kierunku przez równoległy współczynnik skali ${\ Displaystyle k (\ lambda, \ varphi )}$ .

Definicja: Mówimy, że odwzorowanie mapy jest zgodne , jeśli kąt między parą linii przecinających się w punkcie P jest taki sam jak kąt między rzutowanymi liniami w punkcie rzutu P', dla wszystkich par linii przecinających się w punkcie P. Mapa konforemna ma izotropowy współczynnik skali. I odwrotnie, izotropowe współczynniki skali na mapie implikują projekcję konforemną.

Izotropia skali oznacza, że małe elementy są rozciągane jednakowo we wszystkich kierunkach, to znaczy zachowany jest kształt małego elementu. Jest to właściwość ortomorfizmu (z greckiego „właściwy kształt”). Określenie „mały” oznacza, że przy określonej dokładności pomiaru nie można wykryć zmiany współczynnika skali nad elementem. Ponieważ projekcje konforemne mają współczynnik skali izotropowej, nazywane są również projekcjami ortomorficznymi . Na przykład projekcja Mercatora jest konforemna, ponieważ jest skonstruowana tak, aby zachować kąty, a jej współczynnik skali jest izotropowy, będący funkcją tylko szerokości geograficznej: Mercator zachowuje kształt w małych regionach.

Definicja: na rzucie konforemnym ze skalą izotropową punkty, które mają tę samą wartość skali, można połączyć w linie izoskalowe . Nie są one wykreślane na mapach dla użytkowników końcowych, ale pojawiają się w wielu standardowych tekstach. (Patrz Snyder strony 203-206.)

Ułamek reprezentatywny (RF) lub skala główna

Istnieją dwie konwencje stosowane przy ustalaniu równań dowolnej projekcji. Na przykład równokątny występ cylindryczny można zapisać jako

kartografowie:

{\ Displaystyle x = a \ lambda}

{\ Displaystyle y = a \ varphi}

matematycy:

{\ Displaystyle x = \ lambda}

{\ Displaystyle y = \ varphi }

Tutaj przyjmiemy pierwszą z tych konwencji (zgodnie z zastosowaniem w ankietach Snydera). Oczywiście powyższe równania projekcji definiują pozycje na ogromnym cylindrze owiniętym wokół Ziemi, a następnie rozwiniętym. Mówimy, że te współrzędne definiują mapę projekcji , którą należy logicznie odróżnić od faktycznie wydrukowanej (lub przeglądane) mapy. Jeśli definicja skali punktowej w poprzedniej sekcji odnosi się do mapy projekcji, to możemy oczekiwać, że współczynniki skali będą bliskie jedności. Dla normalnych stycznych rzutów cylindrycznych skala wzdłuż równika wynosi k=1 i generalnie skala zmienia się wraz z oddalaniem się od równika. Analiza skali na mapie odwzorowania jest badaniem zmiany k od jego prawdziwej wartości jedności.

Rzeczywiste drukowane mapy są tworzone z mapy projekcji przez stałe skalowanie oznaczone współczynnikiem, takim jak 1:100M (dla map całego świata) lub 1:10000 (dla takich jak plany miast). Aby uniknąć nieporozumień w używaniu słowa „skala”, ten stały ułamek skali nazywany jest ułamkiem reprezentatywnym (RF) drukowanej mapy i należy go identyfikować ze stosunkiem wydrukowanym na mapie. Rzeczywiste wydrukowane współrzędne mapy dla projekcji cylindrycznej o kształcie równokątnym to

wydrukowana mapa:

{\ Displaystyle x = (RF) a \ lambda}

{\ Displaystyle y = (RF) a \ varphi}

Ta konwencja pozwala na wyraźne rozróżnienie wewnętrznego skalowania projekcji i skalowania redukcji.

Od tego momentu ignorujemy RF i pracujemy z mapą projekcji.

Wizualizacja skali punktowej: wskaźnik Tissot

Projekcja tripelowa Winkela ze wskaźnikiem deformacji Tissota

Rozważmy mały okrąg na powierzchni Ziemi wyśrodkowany w punkcie na szerokości $\$ długości geograficznej $displaystyle \ lambda}$ . Ponieważ skala punktowa zmienia się w zależności od położenia i kierunku, rzut okręgu na rzut będzie zniekształcony. Tissota udowodnił, że dopóki zniekształcenie nie będzie zbyt duże, okrąg na rzucie stanie się elipsą. Ogólnie wymiar, kształt i orientacja elipsy będą się zmieniać podczas rzutu. Nałożenie tych elips zniekształceń na projekcję mapy przekazuje sposób, w jaki skala punktów zmienia się na mapie. Elipsa zniekształcenia jest znana jako wskaźnik Tissota . Pokazany tutaj przykład to projekcja potrójna Winkela , standardowa projekcja map świata sporządzona przez Towarzystwo National Geographic . Minimalne zniekształcenie występuje na środkowym południku na 30 stopniach szerokości geograficznej (północ i południe). (Inne przykłady).

Skala punktowa dla normalnych rzutów cylindrycznych kuli

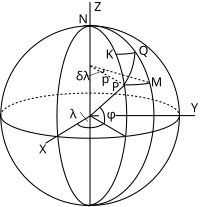
Kluczem do ilościowego zrozumienia skali jest rozważenie nieskończenie małego elementu na kuli. Rysunek przedstawia punkt P na szerokości $λ$ długości geograficznej $\ displaystyle \ lambda}$ na kuli. Punkt Q znajduje się na szerokości geograficznej $Displaystyle$ λ $\ lambda + \ delta \ lambda$ } Proste PK i MQ są łukami południków o długości ${\ Displaystyle a \, \ delta \ varphi}$ $gdzie$ jest kuli, a ${\ Displaystyle \ varphi}$ jest miarą w radianach. Linie PM i KQ są łukami równoległych okręgów o długości $\ Displaystyle (a \ cos \ varphi) \ delta \ lambda}$ $miarą$ w radianach. Wyprowadzając punktu rzutu na P wystarczy wziąć nieskończenie mały element PMQK powierzchni: w granicy Q zbliżającej się do P taki element dąży do nieskończenie małego płaskiego prostokąta.

Nieskończenie małe elementy na kuli i normalny rzut cylindryczny

$Normalne$ $.$ kuli mają są tylko funkcji szerokości Dlatego nieskończenie mały element PMQK na kuli rzutuje na nieskończenie mały element P'M'Q'K', który jest dokładnym prostokątem o podstawie ${\ Displaystyle \ delta x = a \, \ delta \ lambda }$ i wysokość ${\ Displaystyle \ delta y}$ . Porównując elementy na kuli i rzucie, możemy natychmiast wydedukować wyrażenia dla współczynników skali na równoleżnikach i południkach. (Obróbkę skali w ogólnym kierunku można znaleźć poniżej .)

równoległy współczynnik skali

{\ Displaystyle \ quad k \; = \; {\ dfrac {\ delta x} {a \ cos \ varphi \, \ delta \ lambda \, }} = \, \ sec \ varphi \ qquad \ qquad {}}

współczynnik skali południka

{\ Displaystyle \ quad h \; = \; {\ dfrac {\ delta y}{a\,\delta \varphi \,}}={\dfrac {y'(\varphi)}{a}}}

$,$ współczynnik skali jest niezależny od definicji ${\ Displaystyle y (\ varphi)}$ taki sam dla wszystkich normalnych . Warto to zauważyć

na 30 stopniach szerokości geograficznej skala równoległa wynosi

{\ Displaystyle k = \ s 30 ^ {\ circ} = 2/ {\ sqrt {3}} = 1,15}

na 45 stopniach szerokości geograficznej skala równoległa to

{\ Displaystyle k = \ s 45 ^ {\ circ} = {\ sqrt {2}} = 1,414}

na 60 stopniach szerokości geograficznej skala równoległa to

{\ Displaystyle k = \ s 60 ^ {\ circ} = 2}

na 80 stopniach szerokości geograficznej skala równoległa wynosi

{\ Displaystyle k = \ s 80 ^ {\ circ} = 5,76

} szerokość geograficzna 85 stopni równoległa skala to

{\ Displaystyle k = \ sec 85 ^ {\ circ} = 11,5}

Poniższe przykłady ilustrują trzy normalne rzuty cylindryczne iw każdym przypadku zmiana skali wraz z położeniem i kierunkiem jest zilustrowana za pomocą wskaźnika Tissota .

Trzy przykłady normalnego rzutu cylindrycznego

Rzut równokątny

Rzut równoodległy ze wskaźnikiem deformacji Tissota

Projekcja równoprostokątna , znana również jako Plate Carrée (po francusku „płaski kwadrat”) lub (nieco myląco) projekcja równoodległa, jest zdefiniowana przez

{\ Displaystyle x = a \ lambda,}

{\ Displaystyle y = a \ varphi,}

gdzie jest promieniem kuli, $długością$ $\ lambda = 0} ) za {\ Displaystyle a$ od środkowego południka odwzorowania (tutaj jako południk Greenwich w $Displaystyle$ } a to $geograficzna$ . Zauważ, że $\$ są w radianach (uzyskane przez pomnożenie $displaystyle$ stopnia przez współczynnik $\ pi}$ /180). Długość $a$ mieści się w zakresie $]},$ $pi$ szerokość geograficzna się w zakresie ${\ Displaystyle [- \ pi / 2, \ pi / 2]}$ .

Ponieważ poprzednia sekcja daje ${\ Displaystyle y' (\ varphi) = 1}$

skala równoległa

{\ Displaystyle \ quad k \; = \; {\ dfrac {\ delta x} {a \ cos \ varphi \, \ delta \ lambda \, }} = \, \ sec \ varphi \ qquad \ qquad {}}

skala południka

{\ Displaystyle \ quad h \; = \; {\ dfrac {\ delta y} {a \, \delta \varphi \,}}=\,1}

W celu obliczenia skali punktowej w dowolnym kierunku patrz dodatek .

Rysunek ilustruje wskaźnik Tissot dla tej projekcji. Na równiku h=k=1 i elementy kołowe są niezniekształcone w rzucie. Na wyższych szerokościach geograficznych okręgi są zniekształcone w elipsę uzyskaną przez rozciąganie tylko w kierunku równoległym: nie ma zniekształcenia w kierunku południka. Stosunek głównej osi do mniejszej osi wynosi ${\ Displaystyle \ sec \ varphi}$ . Oczywiście pole elipsy zwiększa się o ten sam czynnik.

Pouczające jest rozważenie użycia podziałek słupkowych, które mogą pojawić się na drukowanej wersji tej projekcji. Skala jest prawdziwa (k=1) na równiku, więc pomnożenie jej długości na wydrukowanej mapie przez odwrotność RF (lub głównej skali) daje rzeczywisty obwód Ziemi. Skala słupkowa na mapie jest również rysowana w skali rzeczywistej, więc przeniesienie odległości między dwoma punktami na równiku na skalę słupkową da prawidłową odległość między tymi punktami. To samo dotyczy meridianów. Na równoleżniku innym niż równik skala wynosi ${\ Displaystyle \ sec \ varphi}$ więc kiedy przenosimy odległość z równoległości na skalę słupkową, musimy podzielić odległość na podziałce słupkowej przez ten współczynnik, aby uzyskać odległość między punktami mierzoną wzdłuż równoleżnika (co nie jest rzeczywistą odległością wzdłuż koła wielkiego ) . Na linii na łożysku powiedzmy 45 stopni ( $nie$ się w sposób ciągły wraz z szerokością geograficzną i przeniesienie separacji wzdłuż linii na skalę słupkową odległość związana z rzeczywistą odległością w jakikolwiek prosty sposób. (Ale zobacz dodatek ). Nawet gdyby można było obliczyć odległość wzdłuż tej linii stałego kąta płaskiego, jej znaczenie jest wątpliwe, ponieważ taka linia na rzucie odpowiada skomplikowanej krzywej na kuli. Z tych powodów skale słupkowe na mapach w małej skali muszą być używane z najwyższą ostrożnością.

Projekcja Mercatora

Projekcja Mercatora ze wskaźnikiem deformacji Tissota . (Zniekształcenie wzrasta bez ograniczeń na wyższych szerokościach geograficznych)

Odwzorowanie Mercatora odwzorowuje kulę na prostokąt (o nieskończonej rozpiętości w $-$ ) za pomocą równań

{\ Displaystyle x = a \ lambda \,}

{\ Displaystyle y = a \ ln \ lewo [\ tan \ lewo ({\ Frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right]}

gdzie a $\,}$ $lambda$ i są w poprzednim przykładzie. Ponieważ ${\ Displaystyle y '(\ varphi) = a \ sec \ varphi}$ współczynniki skali to:

skala równoległa

{\ Displaystyle k \; = \; {\ dfrac {\ delta x} {a \ cos \ varphi \, \ delta \ lambda \,}} = \, \ sec \ varphi.} skala

południka

{\ Displaystyle h \; = \; {\ dfrac {\ delta y} {a \, \ delta \ varphi \,}} = \, \ s \ varphi.}

dodatku matematycznym pokazano, że skala punktowa w dowolnym kierunku jest również równa ${\ Displaystyle \ sec \ varphi},$ więc skala jest izotropowa (taka sama we wszystkich kierunkach), a jej wielkość rośnie wraz z szerokością geograficzną jako ${\ Displaystyle \ sec \ varphi}$ . Na diagramie Tissota każdy nieskończenie mały okrągły element zachowuje swój kształt, ale powiększa się coraz bardziej wraz ze wzrostem szerokości geograficznej.

Rzut równego pola Lamberta

Normalny cylindryczny rzut Lamberta o równej powierzchni ze wskaźnikiem deformacji Tissota

Projekcja równego obszaru Lamberta odwzorowuje kulę na skończony prostokąt za pomocą równań

{\ Displaystyle x = a \ lambda \ qquad \ qquad y = a \ sin \ varphi}

gdzie $.$ i są $przykładzie$ jak w poprzednim Ponieważ ${\ Displaystyle y' (\ varphi) = \ cos \ varphi}$ współczynniki skali to

skala równoległa

{\ Displaystyle \ quad k \; = \; {\ dfrac {\ delta x} {a \ cos \ varphi \, \ delta \ lambda \,} } = \, \ sec \ varphi \ qquad \ qquad {}}

skala południka

{\ Displaystyle \ quad h \; = \; {\ dfrac {\ delta y} {a \ ,\delta \varphi \,}}=\,\cos \varphi }

Obliczenie skali punktowej w dowolnym kierunku podano poniżej .

Skale pionowe i poziome kompensują się teraz wzajemnie (hk=1), a na diagramie Tissota każdy nieskończenie mały element kołowy jest zniekształcony w elipsę o tym samym obszarze , co niezniekształcone koła na równiku.

Wykresy współczynników skali

Wykres przedstawia zmienność współczynników skali dla powyższych trzech przykładów. Górny wykres przedstawia izotropową funkcję skali Mercatora: skala na równoleżniku jest taka sama jak skala na południku. Pozostałe wykresy pokazują współczynnik skali południka dla projekcji Equirectangular (h=1) i dla projekcji równej powierzchni Lamberta. Te dwie ostatnie projekcje mają równoległą skalę identyczną jak na wykresie Mercatora. Dla Lamberta zauważ, że skala równoległa (jako Mercator A) rośnie wraz z szerokością geograficzną, a skala południka (C) maleje wraz z szerokością geograficzną w taki sposób, że hk=1, gwarantując ochronę obszaru.

Zmienność skali w projekcji Mercatora

Skala punktowa Mercatora to jedność na równiku, ponieważ jest taka, że pomocniczy cylinder użyty do jej budowy jest styczny do Ziemi na równiku. Z tego powodu zwykły rzut powinien być nazywany stycznym . Skala zmienia się wraz z szerokością geograficzną jako ${\ Displaystyle k = \ sec \ varphi}$ . od ${\ Displaystyle \ sec \ varphi}$ dąży do nieskończoności, gdy zbliżamy się do biegunów, mapa Mercatora jest rażąco zniekształcona na dużych szerokościach geograficznych iz tego powodu odwzorowanie jest całkowicie nieodpowiednie dla map świata (chyba że mówimy o nawigacji i loksodromach ). Jednak na szerokości około 25 stopni wartość ${\ displaystyle \ sec \ varphi}$ wynosi około 1,1, więc Mercator ma dokładność do 10% w pasie o szerokości 50 stopni wyśrodkowanym na równiku. Węższe paski są lepsze: pasek o szerokości 16 stopni (wyśrodkowany na równiku) jest dokładny z dokładnością do 1% lub 1 części na 100.

Standardowym kryterium dobrych map w dużej skali jest to, że dokładność powinna mieścić się w granicach 4 części na 10 000, czyli 0,04%, co odpowiada ${\ displaystyle k = 1,0004}$ . Ponieważ ${\ Displaystyle \ sec \ varphi}$ osiąga tę wartość przy . ${\ Displaystyle \ varphi = 1,62}$ stopni (patrz rysunek poniżej, czerwona linia). Dlatego styczna projekcja Mercatora jest bardzo dokładna w obrębie paska o szerokości 3,24 stopnia wyśrodkowanego na równiku. Odpowiada to odległości północ-południe wynoszącej około 360 km (220 mil). W obrębie tego paska Mercator jest bardzo dobry, bardzo dokładny i zachowuje kształt, ponieważ jest konforemny (zachowuje kąt). Obserwacje te skłoniły do opracowania poprzecznych odwzorowań Merkatora, w których południk traktowany jest „jak równik” odwzorowania, dzięki czemu uzyskujemy dokładną mapę w niewielkiej odległości od tego południka. Takie mapy są dobre dla krajów położonych blisko północy na południe (np Wielkiej Brytanii ), a zestaw 60 takich map jest używany w Universal Transverse Mercator (UTM) . Zauważ, że w obu tych odwzorowaniach (opartych na różnych elipsoidach) równania transformacji dla x i y oraz wyrażenie na współczynnik skali są skomplikowanymi funkcjami zarówno szerokości, jak i długości geograficznej.

Zmienność skali w pobliżu równika dla stycznej (czerwonej) i siecznej (zielonej) projekcji Mercatora.

Projekcje sieczne lub zmodyfikowane

$północ$ projekcji siecznej jest to, że kula jest rzutowana na cylinder, który przecina kulę na dwóch równoleżnikach, powiedzmy na i południe. Oczywiście skala jest teraz prawdziwa na tych szerokościach geograficznych, podczas gdy równoleżniki pod tymi szerokościami geograficznymi są skracane przez projekcję, a ich (równoległy) współczynnik skali musi być mniejszy niż jeden. W rezultacie odchylenie skali od jedności zmniejsza się w szerszym zakresie szerokości geograficznych.

Na przykład jedna możliwa sieczna projekcja Mercatora jest zdefiniowana przez

{\ Displaystyle x = 0,9996a \ lambda \ qquad \ qquad y = 0,9996a \ ln \ lewo (\ tan \ lewo ({\ Frac {\ pi}} {4}} + {\ Frac {\ varphi} {2}} \prawo)\prawo).}

Mnożniki numeryczne nie zmieniają kształtu odwzorowania, ale oznaczają modyfikację współczynników skali:

sieczna skala Mercatora,

{\ Displaystyle \ quad k \; = 0,9996 \ s \ varphi.}

Zatem

skala na równiku to 0,9996,
skala to k = 1 na szerokości geograficznej określonej przez ${\ Displaystyle \ varphi _ {1}}$ gdzie ${\ Displaystyle \ sec \ varphi _ {1} = 1/0,9996 = 1,00004}$ tak, że ${\ Displaystyle \ varphi _ {1} = 1,62}$ stopni,
$_ {2} = 1,0004/0,9996 = 1,0008}$ = 1,0004 na szerokości geograficznej $podanej$ przez varphi ${\ Displaystyle \ varphi _ {2} = 2,29}$ stopni. Dlatego projekcja ma ${\ Displaystyle 1 <k <1,0004}$ , czyli dokładność 0,04%, na szerszym pasku 4,58 stopnia (w porównaniu z 3,24 stopnia dla postaci stycznej).

Ilustruje to dolna (zielona) krzywa na rysunku z poprzedniej sekcji.

Takie wąskie strefy o wysokiej dokładności są używane w projekcji UTM i brytyjskiej OSGB, z których obie są siecznymi, poprzecznymi Merkatorami na elipsoidzie ze skalą na stałej południka środkowego na k = 0,9996 {\ displaystyle k_ $}$ . Linie izoskalowe z $zakrzywionymi liniami około 180 km na wschód i zachód$ południka środkowego Maksymalna wartość współczynnika skali wynosi 1,001 dla UTM i 1,0007 dla OSGB.

Linie skali jednostkowej na szerokości $północ$ i południe), gdzie cylindryczna powierzchnia projekcji przecina kulę, są standardowymi równoległościami projekcji siecznej.

Podczas gdy wąski pasek z ${\ displaystyle | k-1| <0,0004}$ jest ważne dla mapowania z dużą dokładnością w dużej skali, w przypadku map świata do kontrolowania zmienności skali używane są znacznie szersze standardowe równoleżniki. Przykładami są

Behrmanna ze standardowymi równoległościami przy 30N, 30S.
Gall równy obszar ze standardowymi równoleżnikami na 45N, 45S.

Zmienność skali dla projekcji równych obszarów Lamberta (zielony) i Galla (czerwony).

Wykresy skali dla tego ostatniego są pokazane poniżej w porównaniu ze współczynnikami skali równej powierzchni Lamberta. W tym ostatnim równik jest pojedynczym standardowym równoleżnikiem, a skala równoleżnika wzrasta od k = 1, aby skompensować spadek skali południka. Dla Galla skala równoległości zmniejsza się na równiku (do k=0,707), podczas gdy skala południka jest zwiększona (do k=1,414). Powoduje to poważne zniekształcenie kształtu w projekcji Galla-Petersa. (Na kuli ziemskiej Afryka jest mniej więcej tak długa, jak szeroka). Zauważ, że skale południka i równoleżnika są jednością na standardowych równoleżnikach.

Dodatek matematyczny

Nieskończenie małe elementy na kuli i normalny rzut cylindryczny

Dla normalnych rzutów cylindrycznych daje geometria nieskończenie małych elementów

{\ Displaystyle {\ tekst {(a)}} \ quad \ tan \ alfa = {\ Frac {a \ cos \ varphi \, \ delta \ lambda }{a\,\delta \varphi }},}

{\ Displaystyle {\ tekst {(b)}} \ quad \ tan \ beta = {\ Frac {\ delta x} {\ delta y}} = {\ Frac {a \ \ delta \ lambda} {\ delta y }}.}

Zależność między kątami $\ beta}$ jest β $\ displaystyle$

{\ Displaystyle {\ tekst {(c)}} \ quad \ tan \ beta = {\ Frac {a \ sec \ varphi} {y' (\ varphi)}} \ tan \ alfa. \,}

Dla projekcji Mercatora $) = a \ sec \ varphi}$ $:$ kąty są zachowane (Nie jest to zaskakujące, ponieważ jest to relacja używana do wyprowadzenia Mercatora). Dla projekcji równoodległych i Lamberta mamy ${\ Displaystyle y' (\ varphi) = a}$ i $) = a \ cos \ varphi}$ $} styl wyświetlania \varphi}$ odpowiednio, więc związek między a zależy od szerokości geograficznej ${\ Displaystyle \ alpha}$ i ${\ Displaystyle \ beta$ . ${\ Displaystyle \ mu _ {\ alfa}.}$ $α$ gdy nieskończenie mały element PQ tworzy kąt z południkiem o Jest to określone stosunkiem odległości:

{\ Displaystyle \ mu _ {\ alfa} = \ lim _ {Q \ do P}} {\ Frac {P'Q'} {PQ}} = \ lim _ {Q \ do P} {\ frac {\ sqrt { \delta x^{2}+\delta y^{2}}}{\sqrt {a^{2}\,\delta \varphi ^{2}+a^{2}\cos ^{2}\varphi \,\delta \lambda ^{2}}}}.}

$\$ za $i$ ${$ Displaystyle \ \ (b) odpowiednio podaje

{\ Displaystyle \ mu _ {\ alfa} (\ varphi) = \ sec \ varphi \ lewo [{\ Frac {\ sin \ alfa} {\ sin \ beta}} \ prawo].}

$_{\alfa}}$ przypadku rzutów innych niż Mercator musimy najpierw obliczyć $na$ podstawie $i$ φ $\ Displaystyle$ $\ varphi} za pomocą równania (c$ , zanim będziemy mogli . Na przykład rzut równokątny ma tak, że ${\ displaystyle y' = a}$

{\ Displaystyle \ tan \ beta = \ sec \ varphi \ tan \ alfa. \,}

Jeśli weźmiemy pod uwagę linię o stałym nachyleniu $rzucie,$ zarówno odpowiednia wartość $,$ jak i współczynnik skali wzdłuż linii są skomplikowanymi funkcjami . ${\ displaystyle \ varphi$ . Nie ma prostego sposobu przeniesienia ogólnej skończonej separacji na skalę słupkową i uzyskania miarodajnych wyników.

Symbol proporcji

Podczas gdy dwukropek jest często używany do wyrażania proporcji, Unicode może wyrażać symbol specyficzny dla proporcji, lekko podniesiony: U+ 2236 ∶ RATIO ( &ratio; ).

Zobacz też