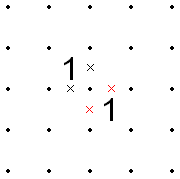Slitherlink

Slitherlink (znany również jako Fences, Takegaki, Loop the Loop, Loopy, Ouroboros, Suriza i Dotty Dilemma) to logiczna łamigłówka opracowana przez wydawcę Nikoli .
Zasady
Slitherlink rozgrywany jest na prostokątnej siatce kropek. W niektórych kwadratach utworzonych przez kropki znajdują się cyfry. Celem jest połączenie poziomo i pionowo sąsiadujących ze sobą kropek tak, aby linie tworzyły prostą pętlę bez luźnych końcówek. Ponadto liczba wewnątrz kwadratu reprezentuje, ile z jego czterech boków to segmenty w pętli.
Zamiast standardowej siatki można zastosować inne typy grafów planarnych , z różną liczbą krawędzi na wierzchołek lub wierzchołków na wielokąt. Te wzory obejmują płatki śniegu, płytki Penrose , Laves i Altair. Zwiększają one złożoność, zmieniając liczbę możliwych ścieżek od skrzyżowania i / lub liczbę boków do każdego wielokąta; ale podobne zasady dotyczą ich rozwiązania.
Metody rozwiązania
Notacja
Ilekroć liczba linii wokół komórki odpowiada liczbie w komórce, inne potencjalne linie muszą zostać wyeliminowane. Jest to zwykle wskazywane przez zaznaczenie X w wierszach, o których wiadomo, że są puste.
Innym przydatnym zapisem podczas rozwiązywania Slitherlink jest łuk o dziewięćdziesiąt stopni między dwiema sąsiednimi liniami, wskazujący, że dokładnie jedna z dwóch musi być wypełniona. Powiązanym zapisem jest podwójny łuk między sąsiednimi liniami, wskazujący, że oba lub żaden z nich nie może być wypełniony. Te oznaczenia nie są konieczne do rozwiązania, ale mogą być pomocne w jego wyprowadzeniu.
Wiele z poniższych metod można podzielić na dwa prostsze etapy za pomocą notacji łukowej.
Dokładnie 2 lub 0 linii w każdym punkcie
Kluczem do wielu dedukcji w Slitherlink jest to, że każdy punkt ma dokładnie dwie połączone z nim linie lub nie ma żadnych linii. Więc jeśli punkt, który znajduje się w środku siatki, a nie na krawędzi lub rogu, ma trzy przychodzące linie, które są na zewnątrz, czwarta również musi być na zewnątrz. Dzieje się tak dlatego, że punkt nie może mieć tylko jednej linii - nie ma z niego drogi wylotowej. Podobnie, jeśli punkt na krawędzi siatki, a nie w rogu, ma dwie przychodzące linie, które są na zewnątrz, trzecia również musi być na zewnątrz. A jeśli róg siatki ma jedną dochodzącą linię, która wychodzi na X, druga również musi być na zewnątrz.
Stosowanie tej prostej zasady prowadzi do coraz bardziej skomplikowanych odliczeń. Znajomość tych prostych wzorców bardzo pomoże w rozwiązywaniu zagadek Slitherlink.
Narożniki
- Jeśli 1 znajduje się w rogu , rzeczywiste linie rogu mogą być na zewnątrz X, ponieważ linia, która weszła do tego rogu, nie mogła go opuścić, chyba że ponownie ominęła 1. Dotyczy to również sytuacji, gdy dwie linie prowadzące do pola 1 w tym samym rogu są na zewnątrz X.
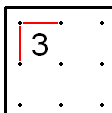
- Jeśli 3 znajduje się w rogu , dwie zewnętrzne krawędzie tego pola można wypełnić, ponieważ w przeciwnym razie powyższa zasada musiałaby zostać złamana.
- Jeśli 2 jest w rogu , dwie linie muszą odchodzić od 2 na granicy.
Zasady dla kwadratów z 1
- Jeśli linia dochodzi do rogu 1 i jeśli jeden z trzech pozostałych kierunków, w których linia może być kontynuowana, ten, który nie jest bokiem 1, jest znanym pustym miejscem, wtedy dwa boki 1 przeciwne do tego rogu mogą być X'd out.
- Obowiązuje to również w odwrotnej kolejności. Oznacza to, że jeśli linia dochodzi do rogu 1, a dwie przeciwległe krawędzie 1 są już na X, linia nie może odejść od 1, ponieważ spowodowałoby to umieszczenie X wokół wszystkich boków 1.
- Jeśli dwie 1 sąsiadują po przekątnej, to z ośmiu segmentów wokół tych dwóch komórek albo „wewnętrzny” zestaw czterech segmentów ma wspólny punkt końcowy (punkt wspólny dla 1), albo drugi „zewnętrzny” zestaw czterech segmentów musi być być X'd out. Zatem jeśli dowolne dwa wewnętrzne lub zewnętrzne segmenty w jednym 1 są X'd, odpowiednie wewnętrzne lub zewnętrzne segmenty drugiego 1 również muszą być X'd.
- Jeśli dwie jedynki sąsiadują wzdłuż krawędzi siatki, linia między nimi może zostać przekreślona na X, ponieważ nie byłoby żadnego kierunku, w którym mogłaby ona kontynuować, gdy dotrze do krawędzi.
Reguła dla kwadratów z 2
Jeśli 2 ma jakąkolwiek otaczającą linię X'd, to linia wchodząca do jednego z dwóch rogów, które nie sąsiadują z linią zewnętrzną X, nie może natychmiast wyjść pod kątem prostym od 2, ponieważ wtedy dwie linie wokół 2 byłyby niemożliwe, a zatem może być X'd. Oznacza to, że linia przychodząca musi być kontynuowana po jednej stronie 2 lub po drugiej. To z kolei oznacza, że druga linia z 2 musi znajdować się na jedynej pozostałej wolnej stronie, przylegającej do pierwotnej linii X, aby można ją było wypełnić.
I odwrotnie, jeśli 2 ma linię po jednej stronie i sąsiednią linię X, to druga linia musi znajdować się po jednej z dwóch pozostałych boków i wychodzić z przeciwległego rogu (w dowolnym kierunku). Jeśli którekolwiek z tych dwóch wyjść jest X, to musi obrać drugą trasę.
Zasady dla kwadratów z 3
- Jeśli 3 sąsiaduje z 0 , poziomo lub pionowo, wówczas wszystkie krawędzie tej 3 mogą być wypełnione, z wyjątkiem jednej dotykającej 0. Ponadto dwie linie prostopadłe do sąsiednich pól mogą być wypełnione.
- Jeśli dwie trójki sąsiadują ze sobą poziomo lub pionowo, ich wspólna krawędź musi być wypełniona, ponieważ jedyną inną opcją jest zamknięty owal, którego nie można połączyć z żadną inną linią. Po drugie, dwie zewnętrzne linie grupy (równoległe do wspólnej linii) muszą być wypełnione. Po trzecie, linia przechodząca przez trójki zawsze będzie zawijać się w kształcie litery „S”. Dlatego linia między trójkami nie może przebiegać w linii prostej, a te boki, które są w linii prostej od linii środkowej, mogą zostać przekreślone.
- Jeśli 3 sąsiaduje z 0 po przekątnej, obie strony 3, które stykają się z rogiem 0, muszą być wypełnione. Dzieje się tak, ponieważ gdyby którakolwiek z tych stron była otwarta, linia kończąca się w rogu 0 nie miałaby miejsca. Jest to podobne do zasady 3 w kącie.
- Podobnie, jeśli 3 ma róg z X w obu kierunkach odchodzących od tego rogu, to obie strony 3, które stykają się z tym rogiem, muszą być wypełnione. Dzieje się tak, ponieważ gdyby jeden z tych dwóch boków 3 był otwarty, drugi musiałby być wypełniony (ponieważ 3 może mieć tylko jeden otwarty bok), ale spotkałby się z 3 X w tym rogu, co jest niemożliwe, ponieważ każdy punkt na siatka musi mieć dokładnie 2 lub 0 linii.
- Jeśli linia dochodzi do rogu 3 , po obu stronach 3 muszą znajdować się linie, z którymi ten róg nie sąsiaduje, ponieważ gdyby jedyne puste miejsce 3 nie sąsiadowało z nim, róg miałby połączone z nim trzy linie . Ponadto odcinek odchodzący od 3 w rogu, do którego prowadzi linia, musi być pusty; gdyby był wypełniony, żaden z pozostałych 2 nieokreślonych boków 3 nie byłby w stanie zawierać linii.
Przekątne 3s i 2s
- Jeśli dwie trójki sąsiadują ze sobą po przekątnej , krawędzie, które nie przechodzą do wspólnego punktu, muszą zostać wypełnione.
- Podobnie, jeśli dwie trójki znajdują się na tej samej przekątnej, ale są oddzielone dowolną liczbą dwójek (i tylko 2), zewnętrzne krawędzie trójek muszą być wypełnione, tak jakby sąsiadowały po przekątnej.
- Jeśli na linii ukośnej znajduje się seria dwójek, a linia ukośna styka się z rogiem dwójki na jednym końcu serii, można narysować pasującą linię ukośną na całej długości serii.
- Jeśli linia dotrze do punktu początkowego (A) przekątnej, która zawiera jedną lub więcej dwójek i kończy się na 3, oba boki odległego rogu (najdalej od punktu A na przekątnej) trójki muszą być wypełnione. Gdyby to nie była prawda, oznaczałoby to, że oba boki najbliższego rogu trójki muszą być wypełnione, co oznaczałoby, że bliskie narożniki wszystkich dwójek muszą być wypełnione, w tym dwójka na początku przekątnej, czyli niemożliwe, ponieważ koliduje z linią, która osiągnęła punkt początkowy (A).
Przekątne 3 i 1
- Jeśli 1 i 3 sąsiadują ze sobą po przekątnej, a zewnętrzne dwa boki 1 są na zewnątrz , to zewnętrzne dwa boki 3 muszą być wypełnione.
- Odwrotnie jest tak samo: jeśli dwa zewnętrzne rogi 3 są wypełnione, to zewnętrzne dwa rogi 1 muszą być wycięte na krzyż.
Przekątne zaczynające się na 2
- Jeśli linia dochodzi do rogu 2, a linia musi przebiegać przez jeden z dwóch łączących się boków 2, to dokładnie jeden z pozostałych dwóch boków 2 musi być wypełniony i ta linia musi przechodzić przez jeden z dwa łączące boki sąsiedniego po przekątnej kwadratu.
Reguła dla regionów zamkniętych
Jeśli region sieci jest zamknięty (tak, że żadne linie nie mogą „uciec”) i nie jest pusty, musi istnieć niezerowa, parzysta liczba linii wchodzących do regionu, które zaczynają się poza regionem. (Nieparzysta liczba linii wchodzących implikuje nieparzystą liczbę zakończeń segmentów wewnątrz regionu, co uniemożliwia połączenie wszystkich końców segmentów. Jeśli nie ma takich linii, linie wewnątrz regionu nie mogą łączyć się z liniami na zewnątrz, co powoduje rozwiązanie niemożliwe.) Często ta zasada eliminuje jedną lub więcej możliwych opcji.
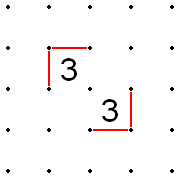
Na poniższym rysunku linia w lewym górnym rogu zamknie prawy górny obszar sieci, niezależnie od tego, czy przebiega w dół, czy w prawo. Linia po prawej stronie (wokół dwóch boków 3) weszła w obszar zamknięty. Aby spełnić regułę, pierwsza linia musi wejść do regionu, a druga linia nie może wejść do regionu po raz drugi. (Ponieważ granica dowolnego zamkniętego regionu zamyka również pozostałą część układanki, regułę można również zastosować do większego, lewego dolnego regionu. Aby zastosować regułę, wystarczy policzyć linie przecinające granicę.)
Twierdzenie o krzywej Jordana
W wyjątkowo trudnej układance można skorzystać z twierdzenia Jordana o krzywej , które mówi, że każda krzywa otwarta, która zaczyna się i kończy poza krzywą zamkniętą, musi przecinać krzywą zamkniętą parzystą liczbę razy. W szczególności oznacza to, że każdy rząd siatki musi mieć parzystą liczbę linii pionowych, a każda kolumna musi mieć parzystą liczbę linii poziomych. Kiedy tylko jeden potencjalny odcinek linii w jednej z tych grup jest nieznany, możesz określić, czy jest on częścią pętli, czy nie, za pomocą tego twierdzenia. Oznacza to również, że jeśli mentalnie prześledzisz dowolną ścieżkę od zewnętrznej krawędzi siatki do innej zewnętrznej krawędzi siatki, ścieżka przetnie zamkniętą krzywą parzystą liczbę razy.
Prostą strategią pomagającą w korzystaniu z tego twierdzenia jest „pomalowanie” (czasami nazywane „cieniem”) obszarów zewnętrznych i wewnętrznych. Kiedy widzisz dwie komórki zewnętrzne lub dwie komórki wewnętrzne obok siebie, wiesz, że nie ma między nimi linii. Odwrotność jest również prawdziwa: jeśli wiesz, że nie ma linii między dwiema komórkami, to te komórki muszą być tego samego „koloru” (zarówno wewnątrz, jak i na zewnątrz). Podobnie, jeśli zewnętrzna komórka i wewnętrzna komórka sąsiadują ze sobą, wiesz, że musi być między nimi wypełniona linia; i znowu sytuacja odwrotna jest prawdziwa.
Zasady łamigłówek, które mają tylko 1 rozwiązanie
- Jeśli istnieją dokładnie dwie możliwe ścieżki, A i B, między dwoma punktami w rozwiązaniu (dwa punkty, które zostały lub muszą zostać osiągnięte przez linie); i jeśli rozwiązanie zawierające A musi również działać z B, a odwrotność nie jest prawdziwa; wtedy B jest poprawną ścieżką, a rozwiązanie musi przechodzić przez punkt zawarty w A, ale nie przez punkt B.
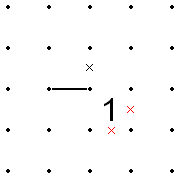
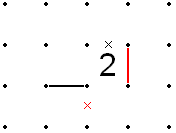
Na poniższym rysunku, jeśli rozwiązanie może przejść przez górną i prawą stronę dwójki, to musi istnieć inne rozwiązanie, które jest dokładnie takie samo, z wyjątkiem tego, że przechodzi przez dolną i lewą stronę dwójki, ponieważ kwadraty do górna i prawa część 2 są nieograniczone (nie zawierają liczb). Ponadto rozwiązanie musi przechodzić przez prawy górny róg dwójki, w przeciwnym razie musi istnieć inne rozwiązanie, które jest dokładnie takie samo, z wyjątkiem tego, że przechodzi przez górną i prawą stronę dwójki.
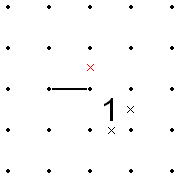
Jeśli w rogu znajduje się 2, a dwa sąsiadujące ze sobą kwadraty nie po przekątnej są nieograniczone, można narysować linie, jak pokazano poniżej. (Na rysunku znak zapytania oznacza dowolną liczbę lub puste miejsce, ale liczbą będzie tylko 2 lub 3. Łamigłówka z tylko jednym rozwiązaniem nie może mieć 2 w rogu z dwoma nieukośnymi, swobodnymi kwadratami i sąsiadujące po przekątnej 0 lub 1.)
- Jeśli istnieją dwie ścieżki między dwoma punktami, tak że rozwiązanie zawierające jeden musi również działać z drugim, wówczas obie ścieżki można wykluczyć.
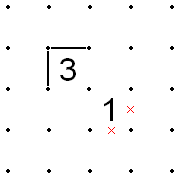
Na poniższym rysunku zakreślone punkty można połączyć linią bezpośrednio między nimi, a także linią przechodzącą przez pozostałe trzy boki kwadratu rozciągającego się na lewo od punktów. Powinno być jasne (z pominięciem czerwonej linii), że dla obu ścieżek pozostała część rozwiązania może być taka sama – ponieważ ograniczenia dla pozostałej części rozwiązania są takie same – więc obie ścieżki są wykluczone.
Historia
Slitherlink to oryginalna łamigłówka Nikoli; po raz pierwszy pojawił się w Puzzle Communication Nikoli # 26 (czerwiec 1989). Redaktor połączył tam dwie oryginalne łamigłówki. Początkowo każdy kwadrat zawierał numer, a krawędzie nie musiały tworzyć pętli.
Gry wideo
Zagadki Slitherlink pojawiły się w grach wideo na kilku platformach. Gra zatytułowana Slither Link została opublikowana w Japonii przez Bandai na przenośną konsolę Wonderswan w 2000 roku. Zagadki Slitherlink zostały dołączone wraz z łamigłówkami Sudoku i Nonogram w Loppi Puzzle Magazine: Kangaeru Puzzle seria gier z Success for the Game Boy Nintendo Power kaseta w 2001 roku Gry Slitherlink były również prezentowane na przenośną konsolę do gier Nintendo DS , a Hudson Soft wypuszcza Puzzle Series Vol. 5: Slitherlink w Japonii 16 listopada 2006 i Agetec , w tym Slitherlink w swojej kompilacji puzzli Nikoli, Brain Buster Puzzle Pak , wydanej w Ameryce Północnej 17 czerwca 2007.
Zobacz też
Linki zewnętrzne
- Angielska strona Nikoli w Slitherlink zarchiwizowana 22.05.2013 w Wayback Machine
- O NP-kompletności układanki Slitherlink - Slitherlink jest NP-kompletny
- Witryna omawiająca inne niż siatki formy Slitherlink, w tym płatki śniegu, penrose, laves i altair
- KwontomLoop - bezpłatna strona z codziennymi łamigłówkami slitherlink o różnym stopniu trudności. Zawiera również system rankingowy z innymi graczami.
- Puzzle Conceptis: Techniki Slitherlink - Ta strona pokazuje kilka zaawansowanych technik rozwiązywania.
- games.softpedia.com — gra Slitherlink do pobrania. To generuje puzzle na różnych poziomach i wymiarach. Możesz także przesłać łamigłówkę (poza witryną), aby ją rozwiązać.
- krazydad.com - Duża liczba książek PDF do wydrukowania z łamigłówkami slitherlink na różnych poziomach dostępnych do pobrania lub grania online.
- [1] - Sugerowany system notacji do dokumentowania łamigłówek slitherlink.
- Loopy — jedna z wielu prostych gier logicznych na komputery stacjonarne dla systemu Windows/Unix autorstwa Simona Tathama .
- All About Slitherlink zapętl łamigłówkę z pętlą
- Najlepsza książka wyjaśniająca zasady i techniki rozwiązywania zagadek oraz historię puzzli