Sprawdzanie, czy moneta jest uczciwa

W statystyce kwestia sprawdzenia, czy moneta jest uczciwa , to taka, której znaczenie polega po pierwsze na przedstawieniu prostego problemu, na podstawie którego można zilustrować podstawowe idee wnioskowania statystycznego , a po drugie na przedstawieniu prostego problemu, który można wykorzystać do porównania różnych konkurencyjne metody wnioskowania statystycznego, w tym teoria decyzji . Praktyczny problem sprawdzenia, czy moneta jest uczciwa, można uznać za łatwy do rozwiązania, wykonując wystarczająco dużą liczbę prób, ale statystyka i teoria prawdopodobieństwa mogą dostarczyć wskazówek dotyczących dwóch rodzajów pytań; w szczególności te dotyczące liczby prób do wykonania i dokładności oszacowania prawdopodobieństwa wyrzucenia orła, wyprowadzonego z danej próby prób.

Uczciwa moneta to wyidealizowane urządzenie losujące z dwoma stanami (zwykle nazywanymi „orłami” i „reszkami” ), których wystąpienie jest równie prawdopodobne. Opiera się na rzucie monetą, powszechnie używanym w sporcie i innych sytuacjach, w których wymagane jest, aby dwie strony miały taką samą szansę na wygraną. Używany jest albo specjalnie zaprojektowany chip, albo częściej zwykła moneta walutowa, chociaż ta ostatnia może być nieco „niesprawiedliwa” ze względu na asymetryczny rozkład masy, co może powodować częstsze występowanie jednego stanu niż drugiego, dając jednej ze stron nieuczciwą przewagę . Dlatego może być konieczne eksperymentalne sprawdzenie, czy moneta jest rzeczywiście „uczciwa” – to znaczy, czy prawdopodobieństwo, że moneta spadnie na którąś ze stron podczas rzucania, wynosi dokładnie 50%. Oczywiście niemożliwe jest wykluczenie arbitralnie niewielkich odchyleń od rzetelności, takich jak można by oczekiwać, że wpłyną tylko na jeden rzut w ciągu całego życia; zawsze jest również możliwe, że nieuczciwa (lub „ stronnicza ”) moneta wypadnie dokładnie 10 reszek w 20 rzutach. W związku z tym każdy test rzetelności musi ustanawiać jedynie pewien stopień zaufania do pewnego stopnia rzetelności (pewne maksymalne obciążenie). W bardziej rygorystycznej terminologii problem polega na określeniu parametrów procesu Bernoulliego , biorąc pod uwagę tylko ograniczoną próbkę prób Bernoulliego .

Preambuła

W tym artykule opisano eksperymentalne procedury określania, czy moneta jest uczciwa, czy nie. Istnieje wiele statystycznych metod analizy takiej procedury eksperymentalnej. Ten artykuł ilustruje dwa z nich.

Obie metody zalecają eksperyment (lub próbę), w którym moneta jest rzucana wiele razy, a wynik każdego rzutu jest rejestrowany. Wyniki można następnie przeanalizować statystycznie, aby zdecydować, czy moneta jest „uczciwa”, czy „prawdopodobnie nieuczciwa”.

• Funkcja gęstości prawdopodobieństwa a posteriori lub PDF ( podejście bayesowskie ). Początkowo prawdziwe prawdopodobieństwo uzyskania określonej strony podczas rzutu monetą jest nieznane, ale niepewność jest reprezentowana przez „ rozkład a priori ”. Teoria wnioskowania bayesowskiego jest wykorzystywana do wyprowadzenia późniejszego rozkładu poprzez połączenie wcześniejszego rozkładu i funkcji wiarygodności , która reprezentuje informacje uzyskane z eksperymentu. Prawdopodobieństwo, że ta konkretna moneta jest „godziwą monetą”, można następnie uzyskać, całkując plik PDF późniejszego rozkładu w odpowiednim przedziale, który reprezentuje wszystkie prawdopodobieństwa, które można uznać za „godziwe” w praktycznym sensie.
• Estymator prawdopodobieństwa prawdziwego ( podejście częstościowe ). Ta metoda zakłada, że ​​eksperymentator może zdecydować się na rzut monetą dowolną liczbę razy. Eksperymentator najpierw decyduje o wymaganym poziomie ufności i dopuszczalnym marginesie błędu. Parametry te określają minimalną liczbę rzutów, które należy wykonać, aby zakończyć doświadczenie.

Ważna różnica między tymi dwoma podejściami polega na tym, że pierwsze podejście przypisuje pewną wagę wcześniejszemu doświadczeniu w rzucaniu monetami, podczas gdy drugie nie. Kwestia, jaką wagę należy przypisać wcześniejszemu doświadczeniu, w zależności od jakości (wiarygodności) tego doświadczenia, jest omawiana w ramach teorii wiarygodności .

Funkcja gęstości prawdopodobieństwa a posteriori

Jedną z metod jest obliczenie późniejszej funkcji gęstości prawdopodobieństwa bayesowskiej teorii prawdopodobieństwa .

Przeprowadza się test, rzucając monetą N razy i zapisując zaobserwowane liczby orłów h i reszek t . Symbole H i T reprezentują bardziej uogólnione zmienne wyrażające odpowiednio liczbę orłów i reszek, które mogły zostać zaobserwowane w eksperymencie. Zatem N = H + T = h + t .

Następnie niech r będzie rzeczywistym prawdopodobieństwem wyrzucenia orła w jednym rzucie monetą. Jest to właściwość badanej monety. Korzystając z twierdzenia Bayesa , gęstość prawdopodobieństwa a posteriori r uwarunkowana h i t wyraża się następująco:

${\ Displaystyle f (r | H = h, T = t) = {\ Frac {\ Pr (H = h | r, N = h + t) \, g (r)} {\ int _ {0} ^ {1}\Pr(H=h|p,N=h+t)\,g(p)\,dp}}.\!}$

gdzie g ( r ) reprezentuje wcześniejszy rozkład gęstości prawdopodobieństwa r , który mieści się w zakresie od 0 do 1.

Wcześniejszy rozkład gęstości prawdopodobieństwa podsumowuje to, co wiadomo o rozkładzie r przy braku jakichkolwiek obserwacji. Założymy, że wcześniejszy rozkład r jest jednorodny w przedziale [0, 1]. Oznacza to, że g ( r ) = 1. (W praktyce bardziej odpowiednie byłoby założenie wcześniejszego rozkładu, który ma znacznie większą wagę w obszarze około 0,5, aby odzwierciedlić nasze doświadczenia z prawdziwymi monetami).

Prawdopodobieństwo wyrzucenia h orłów w N rzutach monetą z prawdopodobieństwem wyrzucenia orłów równym r jest określone przez rozkład dwumianowy :

${\ Displaystyle \ Pr (H = h | r, N = h + t) = {N \ wybierz h} \, r ^ {h} \, (1-r) ^ {t}. \!}$

Podstawiając to do poprzedniej formuły:

${\ Displaystyle f (r | H = h, T = t) = {\ Frac {{N \ wybierz h} \, r ^ {h} \, (1-r) ^ {t}}} {\ int _ { 0}^{1}{N \choose h}\,p^{h}\,(1-p)^{t}\,dp}}={\frac {r^{h}\,(1- r)^{t}}{\int _{0}^{1}p^{h}\,(1-p)^{t}\,dp}}.}$

W rzeczywistości jest to rozkład beta ( koniugat poprzedzający rozkład dwumianowy), którego mianownik można wyrazić za pomocą funkcji beta :

${\ Displaystyle f (r | H = h, T = t) = {\ Frac {1} {\ operatorname {B} (h + 1, t + 1)}} \; r ^ {h} \, (1 -r)^{t}.\!}$

Ponieważ przyjęto jednolity rozkład a priori i ponieważ h i t są liczbami całkowitymi, można to również zapisać za pomocą silni :

${\ Displaystyle f (r | H = h, T = t) = {\ Frac {(h + t + 1)!} {h! \, \, t!}} \; r ^ {h} \, ( 1-r)^{t}.\!}$

Przykład

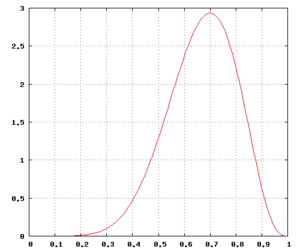
Np. N = 10, h = 7, czyli rzucamy monetą 10 razy i wypada 7 orłów:

${\ Displaystyle f (r | H = 7, T = 3) = {\ Frac {(10 + 1)!} {7! \, \,3!}}\;r^{7}\,(1-r)^{3}=1320\,r^{7}\,(1-r)^{3}\!}$

Wykres po prawej stronie przedstawia funkcję gęstości prawdopodobieństwa r przy założeniu, że w 10 rzutach uzyskano 7 orłów. (Uwaga: r to prawdopodobieństwo wyrzucenia orła w jednym rzucie tą samą monetą.)

Wykres gęstości prawdopodobieństwa f ( r | H = 7, T = 3) = 1320 r ⁷ (1 - r ) ³ z r w zakresie od 0 do 1.

Prawdopodobieństwo dla nieobciążonej monety (zdefiniowanej w tym celu jako taka, której prawdopodobieństwo wypadnięcia reszki wynosi od 45% do 55%)

${\ Displaystyle \ Pr (0,45 <r <0,55) = \ int _ {0,45} ^ { 0,55}f(p|H=7,T=3)\,dp\około 13\%\!}$

jest niewielka w porównaniu z hipotezą alternatywną (obciążona moneta). Jednak nie jest na tyle mały, aby skłonić nas do przekonania, że ​​moneta ma znaczną stronniczość. To prawdopodobieństwo jest nieco wyższe niż nasze założenie prawdopodobieństwa, że ​​moneta była uczciwa, co odpowiada jednolitemu wcześniejszemu rozkładowi, który wynosił 10%. Używając rozkładu wcześniejszego, który odzwierciedla naszą wcześniejszą wiedzę o tym, czym jest moneta i jak działa, rozkład późniejszy nie sprzyjałby hipotezie błędu systematycznego. Jednak liczba prób w tym przykładzie (10 rzutów) jest bardzo mała, a przy większej liczbie prób wybór wcześniejszego rozkładu byłby nieco mniej istotny).

Przy jednolitym priorytecie, późniejszy rozkład prawdopodobieństwa f ( r | H = 7, T = 3) osiąga swój szczyt przy r = h / ( h + t ) = 0,7; ta wartość jest nazywana maksymalnym a posteriori (MAP) oszacowaniem r . Również przy jednolitym priorytecie oczekiwana wartość r pod rozkładem a posteriori wynosi

${\ Displaystyle \ nazwa operatora {E} [r] = \ int _ {0} ^ {1} r \ cdot f (r | H = 7, T = 3) \ \ operatorname {d} r = {\ frac { h+1}{h+t+2}}={\frac {2}{3}}\,.}$

Estymator prawdziwego prawdopodobieństwa

Najlepszym estymatorem rzeczywistej wartości jest estymator $! = {\ frac {h} {h + t}}}$$\ ,$ . Ten estymator ma margines błędu (E), gdzie ${\ displaystyle | pr| <e}$ na określonym poziomie ufności.

Korzystając z tego podejścia, aby zdecydować, ile razy należy rzucić monetą, wymagane są dwa parametry:

1. Poziom ufności oznaczony przedziałem ufności (Z)
2. Maksymalny (dopuszczalny) błąd (E)

• Poziom ufności jest oznaczony przez Z i jest określony przez wartość Z standardowego rozkładu normalnego . Tę wartość można odczytać ze standardowej tabeli statystyk wyników dla rozkładu normalnego. Niektóre przykłady to:

wartość Z	Poziom zaufania	Komentarz
0,6745	daje poziom ufności 50.000 %.	Połowa
1.0000	daje poziom ufności 68,269 %.	Jeden standardowy dev
1,6449	daje poziom ufności 90.000 %.	„Jeden dziewięć”
1,9599	daje poziom ufności 95.000 %.	95 procent
2.0000	daje poziom ufności 95,450 %.	Dwa std dev
2,5759	daje 99.000 % poziom pewności	„Dwie dziewiątki”
3.0000	daje poziom ufności 99,730 %.	Trzy wersje standardowe
3,2905	daje poziom pewności 99,900 %.	„Trzy dziewiątki”
3,8906	daje poziom ufności 99,990 %.	„Cztery dziewiątki”
4.0000	daje poziom ufności 99,993 %.	Czterostopniowa dev
4.4172	daje poziom ufności 99,999 %.	„Pięć dziewiątek”

• Maksymalny błąd (E) jest określony przez $_$ gdzie $jest$ prawdopodobieństwem . _ $jest$ : takie samo rzeczywiste prawdopodobieństwo (uzyskania orłów), jak $w$ sekcji tego artykułu.
• W statystyce oszacowanie części próby (oznaczonej przez p ) ma błąd standardowy określony przez:

${\ Displaystyle s_ {p} = {\ sqrt {\ Frac {p \ (1-p)} {n}}}}$

gdzie n to liczba prób (która została oznaczona przez N w poprzedniej sekcji).

Ta funkcja $standardowego$ ma maksimum przy ${\ Displaystyle p = (1-p) = 0,5$ } . Co więcej, w przypadku rzutu monetą p będzie prawdopodobnie bliskie 0,5, więc rozsądne jest przyjęcie p = 0,5 w następującym przypadku:

${\ Displaystyle s_ {p} \, \!}$

${\ Displaystyle = {\ sqrt {\ Frac {p \, (1-p)} {n}}} \ równoważnik {\ sqrt {\ frac {0.5\times 0.5}{n}}}={\frac {1}{2\,{\sqrt {n}}}}}$

Stąd wartość błędu maksymalnego (E) jest dana przez

${\ Displaystyle E = Z \, s_ {p} = {\ Frac {Z} {2 \, {\ sqrt {n}}}}}$

Rozwiązanie wymaganej liczby rzutów monetą, n ,

${\ Displaystyle n = {\ Frac {Z ^ {2}} {4 \, E ^ {2}}} \!}$

Przykłady

1. Jeśli pożądany jest maksymalny błąd 0,01, ile razy należy rzucić monetą?

${\ Displaystyle n = {\ Frac {Z ^ {2}} {4 \, E ^ {2}}} = {\ Frac {Z ^ {2} {4 \ razy 0,01 ^ {2}}} = 2500 \ Z ^ {2}}$

${\ Displaystyle n = 2500 \,}$ przy poziomie ufności 68,27% (Z = 1)

${\ Displaystyle n = 10000 \,}$ na poziomie ufności 95,45% (Z = 2)

${\ Displaystyle n = 27225 \,}$ na poziomie ufności 99,90% (Z = 3,3)

2. Jeśli moneta zostanie rzucona 10000 razy, jaki jest maksymalny błąd estymatora $orła$$w$ ( rzeczywiste prawdopodobieństwo wyrzucenia rzut monetą)?

${\ Displaystyle E = {\ Frac {Z} {2 \, {\ sqrt {n}}}}}$

${\ Displaystyle E = {\ Frac {Z} 2 \, {\ sqrt {10000}}}} = {\ Frac {Z} {200}}}$

${\ displaystyle E = 0,0050 \,}$ na poziomie ufności 68,27% (Z = 1)

${\ Displaystyle E = 0,0100 \,}$ na poziomie ufności 95,45% (Z = 2)

${\ Displaystyle E = 0,0165 \,}$ na poziomie ufności 99,90% (Z = 3,3)

3. Rzuca się monetą 12000 razy, w wyniku czego wypada 5961 orłów (i 6039 reszek). W jakim przedziale mieści się wartość (prawdziwe prawdopodobieństwo uzyskania orła), jeśli pożądany jest poziom ufności 99,999 $\%$

${\ Displaystyle p = {\ Frac {h} {h + t}} \ = {\ Frac {5961} {12000}} \ = 0,4968}$

Teraz znajdź wartość Z odpowiadającą 99,999% poziomowi ufności.

${\ Displaystyle Z = 4,4172 \, \!}$

Teraz oblicz E

${\ Displaystyle E = {\ Frac {Z} {2 \ {\ sqrt {n}}}} \ = {\ Frac {4,4172} {2 \, {\ sqrt {12000}}}}\,=0,0202}$

Przedział, który zawiera r, to zatem:

${\ displaystyle pE <r <p + E \, \!}$

${\ displaystyle 0,4766 <r <0,5170 \, \!}$

Inne podejścia

Inne podejścia do kwestii sprawdzenia, czy moneta jest uczciwa, dostępne są z wykorzystaniem teorii decyzji , której zastosowanie wymagałoby sformułowania funkcji straty lub funkcji użyteczności opisującej konsekwencje podjęcia danej decyzji. Podejściem, które unika wymagania funkcji straty lub wcześniejszego prawdopodobieństwa (jak w podejściu bayesowskim), jest „próbkowanie akceptacyjne”.

Inne aplikacje

Powyższa analiza matematyczna służąca do określenia, czy moneta jest uczciwa, może być również zastosowana do innych zastosowań. Na przykład:

• Określenie proporcji wadliwych elementów dla produktu poddanego określonemu (ale dobrze określonemu) stanowi. Czasami produkt może być bardzo trudny lub kosztowny w produkcji. Ponadto, jeśli testowanie takich produktów spowoduje ich zniszczenie, należy przetestować minimalną liczbę sztuk. Korzystając z podobnej analizy, można znaleźć funkcję gęstości prawdopodobieństwa wskaźnika defektów produktu.
• Sondaż dwóch partii. Jeśli zostanie przeprowadzona ankieta na małej losowej próbie, w której istnieją tylko dwa wzajemnie wykluczające się wybory, jest to podobne do wielokrotnego rzucania jedną monetą przy użyciu potencjalnie stronniczej monety. Podobną analizę można zatem zastosować do określenia zaufania, jakie należy przypisać faktycznemu stosunkowi oddanych głosów. (Jeśli ludziom pozwoli się wstrzymać się od głosu , analiza musi to uwzględnić, a analogia z rzutem monetą nie do końca się sprawdza).
• Wyznaczanie proporcji płci w dużej grupie gatunków zwierząt. Przy założeniu, że do losowania populacji zostanie pobrana mała próba losowa (tj. mała w porównaniu z całą populacją), analiza jest podobna do określania prawdopodobieństwa wyrzucenia orła w rzucie monetą.

Zobacz też

• Test dwumianowy
• Rzut monetą
• Przedział ufności
• Teoria estymacji
• Statystyki inferencyjne
• Ładowane kostki
• Margines błędu
• Szacowanie punktowe
• Losowość statystyczna

•   Guttman, Wilks i Hunter: Wstępna statystyka inżynierska , John Wiley & Sons, Inc. (1971) ISBN 0-471-33770-6
•   Devinder Sivia: Analiza danych, samouczek bayesowski , Oxford University Press (1996) ISBN 0-19-851889-7