Stożek Steinera

1. Definicja generacji Steinera przekroju stożkowego

Stożek Steinera , a dokładniej generacja stożka Steinera , nazwana na cześć szwajcarskiego matematyka Jakoba Steinera , jest alternatywną metodą definiowania niezdegenerowanej rzutowej sekcji stożkowej w płaszczyźnie rzutowej nad polem .

Zwykła definicja stożka wykorzystuje formę kwadratową (patrz Quadric (geometria rzutowa) ). Inna alternatywna definicja stożka wykorzystuje polaryzację hiperboliczną . Jest to spowodowane KGC von Staudt i czasami nazywane stożkiem von Staudt . Wadą definicji von Staudta jest to, że działa ona tylko wtedy, gdy $)$ tj . .

Definicja stożka Steinera

• $, V}$$\ Displaystyle$ dwa ołówki linii w dwóch punktach linie zawierające $\ Displaystyle U$ i odpowiednio rzutowe, ale nie perspektywiczne odwzorowanie $U)}$$)$$($ { na ${\ Displaystyle B (V)}$ . Następnie punkty przecięcia odpowiednich linii tworzą niezdegenerowany rzutowy przekrój stożkowy (rysunek 1)

2. Mapowanie perspektywiczne między liniami

Odwzorowanie perspektywiczne $ołówka$ na ołówek $1-1$ odpowiedniość $_$ _ _ _ $przecinają$ się na ustalonej linii $,$ jest nazywana osią perspektywy (rysunek 2).

Odwzorowanie projekcyjne jest skończonym produktem odwzorowań perspektywicznych.

$obróci$ przykład: jeśli przesunie się punkt pierwszego diagramu $varphi }$$U$ ołówek linii na i przesunięty ołówek wokół ustalonego kąta, $V}$$\ displaystyle$ następnie przesunięcie (tłumaczenie) i obrót generują odwzorowanie $rzutowe$$w$ punkcie ołówek $w$ . od Twierdzenie o kącie wpisanym otrzymujemy: Punkty przecięcia odpowiednich prostych tworzą okrąg.

Przykładami powszechnie używanych pól są $,$$rzeczywiste$$liczby$ lub zespolone . Konstrukcja działa również na polach skończonych, dostarczając przykładów na skończonych płaszczyznach rzutowych .

Uwaga: Podstawowe twierdzenie o płaszczyznach rzutowych mówi, że odwzorowanie rzutowe w płaszczyźnie rzutowej na pole ( płaszczyzna Pappiana ) jest jednoznacznie określone przez przepisanie obrazów trzech prostych. Oznacza to $podać$ że dla generacji Steinera przekroju stożkowego, oprócz dwóch punktów, tylko obrazy 3 linii Te 5 elementów (2 punkty, 3 linie) jednoznacznie określają przekrój stożka.

Uwaga: Notacja „perspektywa” wynika z podwójnego stwierdzenia: Rzut punktów na linię $ze$$displaystyle$ linię nazywa się perspektywą $b}$ (patrz poniżej ).

3. Przykład generacji Steinera: generacja punktu

Przykład

podano obrazy $rysunek$${\ Displaystyle \ pi (a) = b, \ pi (u) = w, \ pi (w) = v}$ . Odwzorowanie rzutowe $jest$ iloczynem następujących odwzorowań ${\ Displaystyle \ pi _ {b}, \ pi _ {a}}$ : 1) ${\ Displaystyle \ pi _ {b}}$ jest mapowaniem perspektywicznym ołówka w punkcie ${\ Displaystyle U}$ na ołówek w punkcie $}$ osią ${\ displaystyle b$ . 2) ${\ Displaystyle \ pi _ {a}}$ jest odwzorowaniem perspektywicznym ołówka w punkcie na ołówek $Displaystyle$ punkcie z osią $V}$${\ displaystyle a}$ . ${\ Displaystyle \ pi (a) = b, \ pi (u) = w, \ pi (w) = v}$ należy $za$ właściwości . Stąd dla $linii$ obraz ${\ Displaystyle \ pi (g) = \ pi _ {a} \ pi _ {b} (g)}$ można skonstruować, a zatem obrazy dowolnego zestawu punktów. Linie ${\ displaystyle$$v}$ zawierają tylko odpowiednio punkty stożkowe $\$ V $V}$ displaystyle . Stąd ${\ displaystyle u}$ i ${\ displaystyle v}$ są liniami stycznymi wygenerowanego przekroju stożkowego.

Dowód $,$ wynika z przejścia na ograniczenie afiniczne z linią $,$ linią w nieskończoności punktem jako początkiem układu współrzędnych z punktami ${ \displaystyle U,V}$ jako punkty w nieskończoności odpowiednio osi x i y . i punkt ${\ Displaystyle E = (1,1)}$ . Afiniczna część wygenerowanej krzywej wydaje się być hiperbolą y $\ displaystyle y = 1/x}$ .

Uwaga:

1. Generacja przekroju stożkowego Steinera dostarcza prostych metod konstruowania elips , paraboli i hiperboli , które są powszechnie nazywane metodami równoległoboku .
2. Figura pojawiająca się podczas konstruowania punktu (rysunek 3) to 4-punktowa degeneracja twierdzenia Pascala .

Generacja podwójnego stożka Steinera

elipsa podwójna

Generacja podwójnego stożka Steinera

definicja mapowania perspektywicznego

Definicje i podwójne pokolenie

Dualizm (patrz dwoistość (geometria rzutowa) ) płaszczyzny rzutowej polega na zamianie punktów z prostymi i operacjach przecięcia i łączenia . Podwójna struktura płaszczyzny rzutowej jest również płaszczyzną rzutową. Płaszczyzna podwójna płaszczyzny Pappiana jest pappianem i może być również skoordynowana za pomocą jednorodnych współrzędnych. Niezdegenerowany podwójny przekrój stożkowy jest analogicznie zdefiniowany przez formę kwadratową.

Podwójny stożek można wygenerować podwójną metodą Steinera:

• Biorąc pod uwagę zestawy punktów dwóch linii $\$ odwzorowanie rzutowe, ale nie perspektywiczne $displaystyle \ pi}$ u $\ displaystyle u}$ na $\ displaystyle v}$ . Następnie linie łączące odpowiednie punkty tworzą podwójny niezdegenerowany rzutowy przekrój stożkowy.

Odwzorowanie perspektywiczne zbioru $linii$ na $zbiór$$1-1 ) taką, że$ linii jest bijekcją (odpowiedniość łączące odpowiednich punktów przecinają się w stałym punkcie $który$$.$ nazywany środkiem perspektywy (patrz rysunek)

Odwzorowanie projekcyjne to skończona sekwencja odwzorowań perspektywicznych.

Zwykle, gdy mamy do czynienia z podwójnymi i wspólnymi przekrojami stożkowymi, wspólny przekrój stożkowy nazywa się stożkiem punktowym , a podwójny stożkowy stożkiem liniowym .

W przypadku, gdy pole bazowe ma $stożka$ zwanym węzłem lub jądrem stożka. Zatem liczba podwójna niezdegenerowanego stożka punktowego jest podzbiorem punktów linii podwójnej, a nie krzywą owalną (w płaszczyźnie podwójnej). Tak więc tylko w przypadku, gdy $niezdegenerowanego$ podwójna niezdegenerowanego stożka punktowego

Przykłady

Podwójny stożek Steinera zdefiniowany przez dwie perspektywy ${\ Displaystyle \ pi _ {A}, \ pi _ {B}}$

przykład generacji podwójnego stożka Steinera

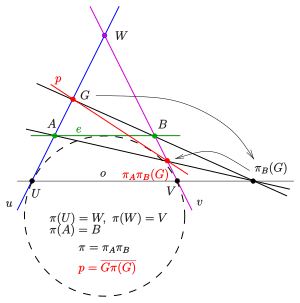
(1) Rzutywność dana przez dwie perspektywy: $}$ są $dwie$ linie z punktem przecięcia i od $displaystyle$$, v$${\ Displaystyle v}$ przez dwie perspektywy ${\ Displaystyle \ pi _ {A}, \ pi _ {B}}$ z centrami ${\ Displaystyle A, B}$ . ${\ Displaystyle \ pi _ {A}}$ odwzorowuje linię ${\ displaystyle u}$ na trzecią linię ${\ displaystyle o}$ , ${\ displaystyle \ pi _ {B}}$ odwzorowuje linię ${\ displaystyle o }$ na linię ${\ displaystyle v}$ (patrz schemat). Punkt ${\ displaystyle W}$ nie może leżeć na liniach ${\ displaystyle {\ overline {AB}}, o}$ . Rzutność ${\ Displaystyle \ pi}$ to kompozycja dwóch perspektyw: ${\ Displaystyle \ \ pi = \ pi _ {B} \ pi _ {A}}$ . Stąd punkt jest odwzorowywany na i $X$$} \ pi _ {A} (X)}$ linia
${\ Displaystyle x = {\ overline {X \ pi (X)}}}$ jest elementem podwójnego stożka zdefiniowanego przez ${\ displaystyle \ pi}$ . (Gdyby $stały$ byłby punktem stałym, $perspektywą$ ).

(2) Dane są trzy punkty i ich obrazy: Poniższy przykład jest podwójnym przykładem podanym powyżej dla stożka Steinera. Obrazy punktów $A) =B,\,\pi (U)=W,\,\pi (W)=V}$ π $)$ . Odwzorowanie rzutowe ${\ Displaystyle \ pi}$ może być reprezentowany przez iloczyn następujących perspektyw: ${\ displaystyle \ pi _ {B}, \ pi _ {A}}$ :

1. $_ {B}}$${ \ Displaystyle \$ pi $jest$ perspektywą zbioru punktów linii $.$ punktów linii ze
2. $_ {A}}$$Displaystyle \$$pi$$jest$ perspektywą zbioru punktów linii punktów linii ze .

Łatwo sprawdzić, czy odwzorowanie rzutowe spełnia ${\ Displaystyle \ pi = \ pi _ {A} \ pi _ {B}}$ spełnia ${\ Displaystyle \ pi (A) = B, \, \ pi (U) = W, \, \ pi (W) = V}$ . Stąd dla dowolnego dowolnego punktu obraz $\ displaystyle G$${\ Displaystyle \ pi (G) = \ pi _ {A} \ pi _ {B} (G)}$ można skonstruować i linię ${\ Displaystyle {\ overline {G\pi (G)}}}$ jest elementem niezdegenerowanego podwójnego przekroju stożkowego. Ponieważ punkty i ${\ displaystyle$$}$ są zawarte w liniach odpowiednio, punkty ${\ displaystyle u}$ , $\ displaystyle v}$${\ displaystyle U}$ i $displaystyle V}$$}$ są punktami stożka, a linie stycznymi w $displaystyle U,$ .

Stożki wewnętrzne w geometrii padania liniowego

Konstrukcja Steinera definiuje stożki w płaskiej geometrii liniowej padania (dwa punkty wyznaczają co najwyżej jedną linię, a dwie linie przecinają się co najwyżej w jednym punkcie) wewnętrznie, to znaczy używając tylko grupy kolineacji. W szczególności ${\ Displaystyle E (T, P)}$$jest$ stożkiem w punkcie przez kolineację , składającą się z przecięć $}$${\ Displaystyle$ i $\ Displaystyle T (L)}$${\ Displaystyle P$ dla wszystkich linii do $}$ . Jeśli ${\ Displaystyle T (P) = P}$ lub ${\ Displaystyle T (L) = L}$$dla$ pewnego stożek jest zdegenerowany . Na przykład w rzeczywistej płaszczyźnie współrzędnych typ afiniczny (elipsa, parabola, hiperbola) $T, P)}$$T}$ jest określony przez ślad i wyznacznik składnika macierzy niezależnego od $displaystyle$ .

$składa$ grupa kolineacji rzeczywistej płaszczyzny hiperbolicznej się z izometrii W konsekwencji stożki wewnętrzne obejmują mały, ale zróżnicowany podzbiór stożków ogólnych , krzywych uzyskanych z przecięcia stożków rzutowych z domeną hiperboliczną. Ponadto, w przeciwieństwie do płaszczyzny euklidesowej, nie ma nakładania się między bezpośrednim zachowaniem orientacji - a mi ${\ Displaystyle E (T, P)}$ T $\ Displaystyle T}$ naprzeciwko mi $\ Displaystyle E (T, P)}$ - ${\ Displaystyle T}$ odwraca orientację. Przypadek bezpośredni obejmuje centralne (dwie prostopadłe osie symetrii) i niecentralne, podczas gdy każdy stożek przeciwny jest centralny. Chociaż bezpośrednie i przeciwstawne stożki centralne nie mogą być przystające, są one powiązane quasi-symetrią zdefiniowaną w kategoriach dopełniających się kątów równoległości. Zatem w każdym odwrotnym modelu ${\ Displaystyle \ mathbb {H} ^ {2}}$ , każdy bezpośredni stożek centralny jest dwuracjonalnie równoważny przeciwległemu stożkowi centralnemu. W rzeczywistości środkowe stożki reprezentują wszystkie krzywe rodzaju 1 z niezmiennym kształtem rzeczywistym ${\ displaystyle j \ geq 1}$ . Minimalny zestaw przedstawicieli uzyskuje się z centralnych bezpośrednich stożków ze wspólnym środkiem i osią symetrii, przy czym niezmiennik kształtu jest funkcją mimośrodu , zdefiniowanego w kategoriach odległości między ${\ displaystyle P}$ i ${ \displaystyle T(P)}$ . Ortogonalne trajektorie tych krzywych reprezentują wszystkie krzywe rodzaju 1 z $sześcienne$ lub dwukołowe kwarce. Korzystając z prawa dodawania krzywych eliptycznych na każdej trajektorii, każdy ogólny stożek centralny w $trajektorię$ jako suma dwóch wewnętrznych stożków przez dodanie par punktów, w których stożki przecinają każdą .

Notatki

• Coxeter, HSM (1993), Prawdziwa płaszczyzna rzutowa , Springer Science & Business Media
• Hartmann, Erich, Planar Circle Geometries, an Introduction to Moebius-, Laguerre- and Minkowski Planes (PDF) , pobrane 20 września 2014 r. (PDF; 891 kB).
•   Merserve, Bruce E. (1983) [1959], Podstawowe pojęcia geometrii , Dover, ISBN 0-486-63415-9