Szary wykres
| Wykres Graya | |
|---|---|
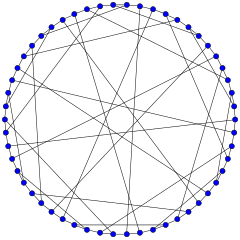 Wykres Graya
| |
| Nazwany po | Marion Cameron Grey |
| Wierzchołki | 54 |
| Krawędzie | 81 |
| Promień | 6 |
| Średnica | 6 |
| Obwód | 8 |
| Automorfizmy | 1296 |
| Liczba chromatyczna | 2 |
| Indeks chromatyczny | 3 |
| Grubość książki | 3 |
| Numer kolejki | 2 |
| Nieruchomości |
Sześcienny półsymetryczny hamiltonian dwudzielny |
| Tabela wykresów i parametrów | |
W matematycznej dziedzinie teorii grafów graf Graya jest nieskierowanym grafem dwudzielnym z 54 wierzchołkami i 81 krawędziami . Jest to graf sześcienny : każdy wierzchołek styka się dokładnie z trzema krawędziami. Został odkryty przez Marion C. Gray w 1932 r. (niepublikowane), a następnie odkryty niezależnie przez Bouwera w 1968 r. w odpowiedzi na pytanie zadane przez Jona Folkmana w 1967 r. Graf Graya jest interesujący jako pierwszy znany przykład wykresu sześciennego mającego właściwość algebraiczną będąc krawędzią, ale nie wierzchołkiem przechodnim (patrz poniżej).
Graf Graya ma liczbę chromatyczną 2, indeks chromatyczny 3, promień 6 i średnicę 6. Jest to również graf niepłaski połączony z 3 wierzchołkami i 3 krawędziami .
Budowa
Graf Graya można zbudować ( Bouwer 1972 ) z 27 punktów siatki 3 × 3 × 3 i 27 równoległych do osi linii przechodzących przez te punkty. Ten zbiór punktów i linii tworzy konfigurację rzutową : przez każdy punkt przechodzą dokładnie trzy proste, a na każdej prostej znajdują się dokładnie trzy punkty. Wykres Graya jest wykresem Leviego dla tej konfiguracji; ma wierzchołek dla każdego punktu i każdej linii konfiguracji oraz krawędź dla każdej pary punktu i prostej, które się stykają. Ta konstrukcja uogólnia (Bouwer 1972) do dowolnego wymiaru n ≥ 3, dając an n -wartościowy graf Leviego o właściwościach algebraicznych podobnych do wykresu Graya. W (Monson, Pisanski, Schulte, Ivic-Weiss 2007) wykres Graya pojawia się jako inny rodzaj wykresu Leviego dla krawędzi i trójkątnych ścian pewnego lokalnie toroidalnego abstrakcyjnego regularnego 4-politopu. Jest to zatem pierwszy z nieskończonej rodziny podobnie skonstruowanych grafów sześciennych. Podobnie jak w przypadku innych grafów Leviego, jest to graf dwudzielny , z wierzchołkami odpowiadającymi punktom po jednej stronie dwupodziału i wierzchołkami odpowiadającymi liniom po drugiej stronie.
Marušič i Pisanski (2000) podają kilka alternatywnych metod konstruowania grafu Graya. Podobnie jak w przypadku każdego wykresu dwudzielnego, nie ma cykli o nieparzystej długości , a także nie ma cykli o czterech lub sześciu wierzchołkach, więc obwód wykresu Graya wynosi 8. Najprostsza zorientowana powierzchnia, na której można osadzić wykres Graya, ma rodzaj 7 ( Marušič, Pisanski & Wilson 2005 ).
Wykres Graya jest hamiltonowski i można go skonstruować z notacji LCF :
![[-25,7,-7,13,-13,25]^{9}.\](https://wikimedia.org/api/rest_v1/media/math/render/svg/014e670206b76bab2513b807e955533d50c3efb0)
Jako graf sześcienny Hamiltona ma indeks chromatyczny trzy.
Właściwości algebraiczne
Grupa automorfizmu grafu Graya jest grupą rzędu 1296. Działa przechodnie na krawędziach grafu, ale nie na jego wierzchołkach: istnieją symetrie prowadzące każdą krawędź do dowolnej innej krawędzi, ale nie prowadzące każdego wierzchołka do żadnego innego wierzchołka. Wierzchołki odpowiadające punktom podstawowej konfiguracji mogą być symetryczne tylko względem innych wierzchołków odpowiadających punktom, a wierzchołki odpowiadające liniom mogą być symetryczne tylko względem innych wierzchołków odpowiadających liniom. Dlatego wykres Graya jest grafem półsymetrycznym , najmniejszym możliwym grafem półsymetrycznym sześciennym.
Charakterystyczny wielomian wykresu Graya to
- Bouwer , IZ ( 1968 ) _ _ _
- Bouwer, IZ (1972), „Na krawędzi, ale nie wierzchołkach przechodnich regularnych grafów”, Journal of Combinatorial Theory , Seria B , 12 : 32–40, doi : 10.1016/0095-8956 (72) 90030-5 .
- Folkman, J. (1967), „Regularne liniowe symetryczne wykresy”, Journal of Combinatorial Theory , 3 (3): 533–535, doi : 10.1016 / S0021-9800 (67) 80069-3 .
- Marušič, Dragan ; Pisanski, Tomaž (2000), "The Grey graph revisited", Journal of Graph Theory , 35 : 1–7, doi : 10.1002/1097-0118 (200009) 35: 1 <1:: AID-JGT1> 3.0.CO; 2-7 .
- Marušič, Dragan ; Pisanski, Tomaž ; Wilson, Steve (2005), „Rodzaj wykresu Graya to 7”, European Journal of Combinatorics , 26 (3–4): 377–385, doi : 10.1016/j.ejc.2004.01.015 .
- Monson, B.; Pisański T. ; Schulte, E.; Ivic-Weiss, A. (2007), „Wykresy półsymetryczne z Polytopes”, Journal of Combinatorial Theory , Seria A , 114 (3): 421–435, arXiv : math/0606469 , doi : 10.1016/j.jcta.2006.06. 007 , S2CID 10203794