Teoria ogniw słonecznych

Teoria ogniw słonecznych wyjaśnia proces, w którym energia świetlna w fotonach jest przekształcana w prąd elektryczny, gdy fotony uderzają w odpowiednie urządzenie półprzewodnikowe . Badania teoretyczne mają praktyczne zastosowanie, ponieważ przewidują podstawowe ograniczenia ogniw słonecznych i dają wskazówki dotyczące zjawisk, które przyczyniają się do strat i wydajności ogniw słonecznych .

Schemat pasmowy ogniwa słonecznego, odpowiadający bardzo niskiemu prądowi (poziomy poziom Fermiego ), bardzo niskiemu napięciu (metalowe pasma walencyjne na tej samej wysokości), a zatem bardzo słabemu oświetleniu

Wyjaśnienie robocze

1. Fotony w świetle słonecznym uderzają w panel słoneczny i są pochłaniane przez materiały półprzewodnikowe.
2. Elektrony (naładowane ujemnie) są wybijane ze swoich atomów, gdy są wzbudzone. Ze względu na ich specjalną strukturę i materiały w ogniwach słonecznych, elektrony mogą poruszać się tylko w jednym kierunku. Struktura elektronowa materiałów jest bardzo ważna dla przebiegu procesu i często w różnych warstwach stosuje się krzem zawierający niewielkie ilości boru lub fosforu .
3. Szereg ogniw słonecznych przekształca energię słoneczną w użyteczną ilość prądu stałego (DC).

Fotogeneracja nośników ładunku

Kiedy foton uderza w kawałek półprzewodnika, może się zdarzyć jedna z trzech rzeczy:

1. Foton może przejść bezpośrednio przez półprzewodnik — dzieje się tak (ogólnie) w przypadku fotonów o niższej energii.
2. Foton może odbijać się od powierzchni.
3. Foton może zostać zaabsorbowany przez półprzewodnik, jeśli energia fotonu jest większa niż wartość pasma wzbronionego . To generuje parę elektron-dziura i czasami ciepło w zależności od struktury pasma.

Schemat pasmowy krzemowego ogniwa słonecznego, odpowiadający bardzo niskiemu prądowi (poziomy poziom Fermiego ), bardzo niskiemu napięciu (metalowe pasma walencyjne na tej samej wysokości), a zatem bardzo słabemu oświetleniu

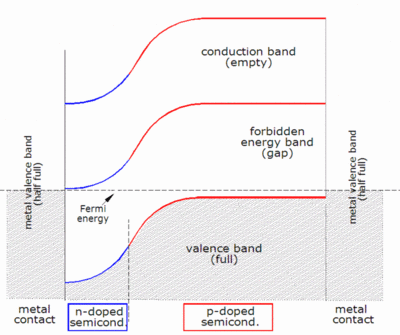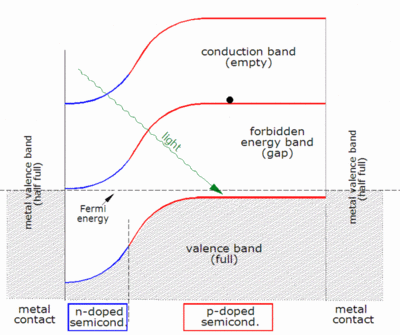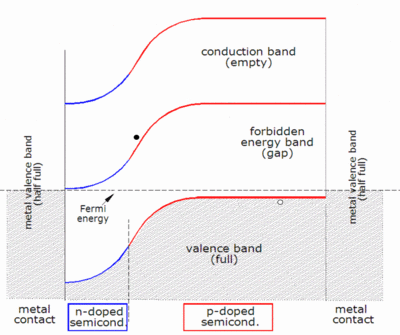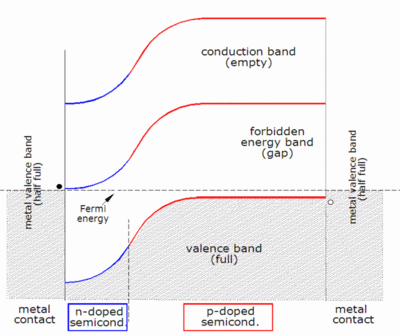
Kiedy foton jest absorbowany, jego energia jest przekazywana elektronowi w sieci krystalicznej. Zwykle ten elektron jest w paśmie walencyjnym . Energia przekazana elektronowi przez foton „pobudza” go do pasma przewodnictwa gdzie można swobodnie poruszać się w półprzewodniku. Sieć wiązań kowalencyjnych, której częścią był wcześniej elektron, ma teraz o jeden elektron mniej. Nazywa się to dziurą i ma ładunek dodatni. Obecność brakującego wiązania kowalencyjnego umożliwia związanym elektronom sąsiednich atomów przejście do „dziury”, pozostawiając kolejną dziurę za sobą, propagując w ten sposób dziury w sieci w kierunku przeciwnym do ruchu elektronów ujemnych. Można powiedzieć, że fotony zaabsorbowane w półprzewodniku tworzą pary elektron-dziura.

Foton musi mieć tylko energię większą niż pasmo wzbronione, aby wzbudzić elektron z pasma walencyjnego do pasma przewodnictwa. Jednak widmo częstotliwości Słońca jest zbliżone do widma ciała doskonale czarnego przy około 5800 K i jako takie, większość promieniowania słonecznego docierającego do Ziemi składa się z fotonów o energiach większych niż pasmo wzbronione krzemu (1,12 eV), co jest wartością zbliżoną do idealnej dla ziemskiego ogniwa słonecznego (1,4 eV). Te fotony o wyższej energii zostaną pochłonięte przez krzemowe ogniwo słoneczne, ale różnica energii między tymi fotonami a pasmem wzbronionym krzemu zostanie przekształcona w ciepło (poprzez wibracje sieci — zwane fononami), a nie w użyteczną energię elektryczną.

Węzeł pn

Główne artykuły: półprzewodnik i złącze pn

Najbardziej znane ogniwo słoneczne jest skonfigurowane jako złącze pn o dużej powierzchni wykonane z krzemu. W uproszczeniu można sobie wyobrazić bezpośredni kontakt warstwy krzemu typu n z warstwą krzemu typu p. Domieszkowanie typu n wytwarza ruchome elektrony (pozostawiając dodatnio naładowane donory), podczas gdy domieszkowanie typu p wytwarza ruchome dziury (i ujemnie naładowane akceptory). domieszkę typu -na jedną stronę płytki typu p (lub odwrotnie).

Jeśli kawałek krzemu typu p zostanie umieszczony w bliskim kontakcie z kawałkiem krzemu typu n, wówczas następuje dyfuzja elektronów z obszaru o wysokim stężeniu elektronów (strona złącza typu n) do obszaru o niskim stężenie elektronów (strona złącza typu p). Kiedy elektrony dyfundują do strony typu p, każdy z nich anihiluje dziurę, powodując, że ta strona jest naładowana ujemnie (ponieważ teraz liczba ruchomych dziur dodatnich jest teraz mniejsza niż liczba akceptorów ujemnych). Podobnie, dziury dyfundujące do strony typu n sprawiają, że jest ona bardziej naładowana dodatnio. Jednak (w przypadku braku obwodu zewnętrznego) ten prąd dyfuzyjny nośników nie trwa w nieskończoność, ponieważ ładunek gromadzący się po obu stronach złącza wytwarza pole elektryczne , które przeciwdziała dalszemu rozprzestrzenianiu się kolejnych ładunków. Ostatecznie równowaga zostaje osiągnięta, gdy prąd netto wynosi zero, pozostawiając obszar po obu stronach złącza, w którym elektrony i dziury dyfundowały przez złącze i anihilowały się nawzajem, zwany obszarem wyczerpania, ponieważ praktycznie nie zawiera on ruchomych nośników ładunku . Jest również znany jako obszar ładunku kosmicznego , chociaż ładunek kosmiczny rozciąga się nieco dalej w obu kierunkach niż obszar wyczerpania.

Po ustaleniu równowagi pary elektron-dziura generowane w obszarze zubożonym są rozdzielane przez pole elektryczne, przy czym elektron jest przyciągany do dodatniej strony typu n, a dziury do ujemnej strony typu p, zmniejszając ładunek (i pole elektryczne ) zbudowany przez właśnie opisaną dyfuzję. Jeśli urządzenie jest odłączone (lub obciążenie zewnętrzne jest bardzo wysokie), wówczas prąd dyfuzyjny ostatecznie przywróci ładunek równowagi, przenosząc elektron i dziurę z powrotem przez złącze, ale jeśli podłączone obciążenie jest wystarczająco małe, elektrony wolą krążyć wokół obwód zewnętrzny, próbując przywrócić równowagę, wykonując po drodze pożyteczną pracę.

Separacja nośników ładunku

Istnieją dwie przyczyny ruchu i separacji nośników ładunku w ogniwie słonecznym:

1. dryf nośników napędzany polem elektrycznym, przy czym elektrony są wypychane w jedną stronę, a dziury w drugą
2. dyfuzja nośników ze stref o wyższym stężeniu nośników do stref o niższym stężeniu nośników (zgodnie z gradientem potencjału chemicznego).

Te dwie „siły” mogą działać przeciwko sobie w dowolnym punkcie komórki. Na przykład elektron poruszający się przez złącze z regionu p do regionu n (jak na schemacie na początku tego artykułu) jest popychany przez pole elektryczne w kierunku przeciwnym do gradientu stężeń. To samo dotyczy otworu poruszającego się w przeciwnym kierunku.

Najłatwiej zrozumieć, w jaki sposób generowany jest prąd, biorąc pod uwagę pary elektron-dziura, które powstają w strefie zubożenia, czyli tam, gdzie występuje silne pole elektryczne. Elektron jest popychany przez to pole w stronę n, a dziura w stronę p. (Jest to przeciwne do kierunku prądu w diodzie spolaryzowanej do przodu, takiej jak dioda elektroluminescencyjna w działaniu.) Kiedy para jest tworzona poza strefą ładunku kosmicznego, gdzie pole elektryczne jest mniejsze, dyfuzja działa również w celu przemieszczania nośników, ale złącze nadal odgrywa rolę, przemiatając wszelkie elektrony, które do niego docierają, ze strony p do po stronie n i poprzez zamiatanie wszelkich otworów, które do niej docierają, od strony n do strony p, tworząc w ten sposób gradient stężenia poza strefą ładunku kosmicznego.

W grubych ogniwach słonecznych pole elektryczne w obszarze aktywnym poza strefą ładunku kosmicznego jest bardzo małe, więc dominującym sposobem separacji nośników ładunku jest dyfuzja. W tych komórkach długość dyfuzji nośników mniejszościowych (długość, jaką mogą pokonać nośniki fotogenerowane przed rekombinacją) musi być duża w porównaniu z grubością komórki. W ogniwach cienkowarstwowych (takich jak krzem amorficzny) długość dyfuzji nośników mniejszościowych jest zwykle bardzo krótka z powodu istnienia defektów, dlatego dominującym rozdziałem ładunku jest dryf, napędzany przez pole elektrostatyczne złącza, które rozciąga się do całej grubości komórki.

Gdy przewoźnik mniejszościowy wejdzie w obszar dryfu, jest „przesuwany” przez skrzyżowanie i po drugiej stronie skrzyżowania staje się nosicielem większościowym. Ten prąd wsteczny jest prądem generacyjnym, zasilanym zarówno termicznie, jak i (jeśli występuje) przez absorpcję światła. Z drugiej strony nośniki większościowe są wypychane w obszar dryfu przez dyfuzję (wynikającą z gradientu stężeń), co prowadzi do prądu przewodzenia; tylko nośniki większościowe o najwyższych energiach (w tzw. ogonie Boltzmanna; por. statystyka Maxwella-Boltzmanna ) może w pełni przekroczyć obszar dryfu. Dlatego rozkład nośników w całym urządzeniu jest regulowany przez dynamiczną równowagę między prądem wstecznym a prądem przewodzenia.

Podłączenie do obciążenia zewnętrznego

Rezystancyjne styki metal -półprzewodnik są wykonane zarówno po stronie typu n, jak i typu p ogniwa słonecznego, a elektrody są podłączone do zewnętrznego obciążenia. Elektrony, które są tworzone po stronie typu n lub po stronie typu p, „zbierane” przez złącze i przenoszone na stronę typu n, mogą przemieszczać się przez przewód, zasilać obciążenie i przechodzić przez przewód aż dotrą do styku półprzewodnik-metal typu p. Tutaj rekombinują z dziurą, która została utworzona jako para elektron-dziura po stronie typu p ogniwa słonecznego lub dziura, która została przeciągnięta przez złącze od strony typu n po utworzeniu tam.

Zmierzone napięcie jest równe różnicy poziomów quasi-Fermiego nośników większościowych (elektrony w części typu n i dziury w części typu p) na dwóch zaciskach.

Równoważny obwód ogniwa słonecznego

Schematyczny symbol ogniwa słonecznego

Równoważny obwód ogniwa słonecznego

Aby zrozumieć elektroniczne zachowanie ogniwa słonecznego, warto stworzyć model, który jest elektrycznie równoważny i jest oparty na dyskretnych idealnych elementach elektrycznych, których zachowanie jest dobrze zdefiniowane. Idealne ogniwo słoneczne może być modelowane przez źródło prądu połączone równolegle z diodą ; w praktyce żadne ogniwo słoneczne nie jest idealne, więc do modelu dodaje się rezystancję bocznikową i składową rezystancji szeregowej. Wynikowy równoważny obwód ogniwa słonecznego pokazano po prawej stronie. Po lewej stronie pokazano również schematyczne przedstawienie ogniwa słonecznego do wykorzystania na schematach obwodów.

Równanie charakterystyczne

Z równoważnego obwodu widać, że prąd wytwarzany przez ogniwo słoneczne jest równy prądowi wytwarzanemu przez źródło prądu, minus prąd przepływający przez diodę, minus prąd przepływający przez rezystor bocznikowy:

${\ Displaystyle I = ja _ {\ tekst {L}} -I _ {\ tekst {D}} -I _ {\ tekst {SH}}}$

Gdzie

• I , prąd wyjściowy ( amper )
• I _L , prąd fotogenerowany (amper)
• I _D , prąd diody (amper)
• I _SH , prąd bocznikowy (amper).

Prąd przepływający przez te elementy jest regulowany przez napięcie na nich:

${\ Displaystyle V _ {\ tekst {j}} = V + IR _ {\ tekst {S}}}$

Gdzie

• V _j , napięcie na diodzie i rezystorze R _SH ( wolty )
• V , napięcie na zaciskach wyjściowych (wolty)
• I , prąd wyjściowy (amper)
• RS _, rezystancja szeregowa ( Ω ).

Z równania diody Shockleya wynika , że ​​prąd płynący przez diodę wynosi:

${\ Displaystyle I _ {\ tekst {D}} = I_ {0} \ lewo \ {\ exp \ lewo [{\ Frac {V_ {\ tekst {j}}}{nV_{\text{T}}}}\right]-1\right\}}$

Gdzie

• ₀ I , wsteczny prąd nasycenia (amper)
• n , współczynnik idealności diody (1 dla idealnej diody)
• q , ładunek elementarny
• k , stała Boltzmanna
• T , temperatura bezwzględna
• ${\ Displaystyle V _ {\ tekst {T}} = kT / q,}$ napięcie termiczne . W temperaturze 25 ° C ${\ Displaystyle V _ {\ tekst {T}} \ około 0,0259}$ woltów.

Zgodnie z prawem Ohma prąd płynący przez bocznik wynosi:

${\ Displaystyle I _ {\ tekst {SH}} = {\ Frac {V _ {\ tekst {j}}} {R _ {\ tekst {SH}}}}}$

Gdzie

• R _SH , rezystancja bocznika (Ω).

Podstawienie ich do pierwszego równania daje charakterystyczne równanie ogniwa słonecznego, które wiąże parametry ogniwa słonecznego z prądem i napięciem wyjściowym:

${\ Displaystyle I = I _ {\ tekst {L}} -I_ {0} \ lewo \ {\ exp \ lewo [{\ Frac {V + IR_ {\ tekst {S}}} {nV_ {\ tekst {T} }}}\right]-1\right\}-{\frac {V+IR_{\text{S}}}{R_{\text{SH}}}}.}$

Alternatywne wyprowadzenie daje równanie o podobnym wyglądzie, ale z V po lewej stronie. Te dwie alternatywy to tożsamości ; to znaczy dają dokładnie takie same wyniki.

₀ Ponieważ parametrów I , n , R _S i R _SH nie można zmierzyć bezpośrednio, najczęstszym zastosowaniem równania charakterystycznego jest regresja nieliniowa w celu wyodrębnienia wartości tych parametrów na podstawie ich łącznego wpływu na zachowanie ogniw słonecznych.

Gdy R _S nie wynosi zero, powyższe równanie nie daje bezpośrednio prądu I , ale można je rozwiązać za pomocą funkcji W Lamberta :

${\ Displaystyle I = {\ Frac {(I _ {\ tekst {L}} + I_ {0}) -V / R _ {\ tekst {SH}}} {1 + R_ {\ tekst {S}} / R_ { \text{SH}}}}-{\frac {nV_{\text{T}}}{R_{\text{S}}}}W\left({\frac {I_{0}R_{\text{ S}}}{nV_{\text{T}}(1+R_{\text{S}}/R_{\text{SH}})}}\exp \left({\frac {V}{nV_{ \text{T}}}}\left(1-{\frac {R_{\text{S}}}{R_{\text{S}}+R_{\text{SH}}}}\right)+ {\frac {(I_{\text{L}}+I_{0})R_{\text{S}}}{nV_{\text{T}}(1+R_{\text{S}}/R_ {\text{SH}}}}}\right)\right)}$

Gdy z ogniwem używane jest obciążenie zewnętrzne, jego rezystancję można po prostu dodać do R _S i V ustawić na zero, aby znaleźć prąd.

Gdy R _SH jest nieskończony, istnieje rozwiązanie dla V dla dowolnego $}$ niż ${\ Displaystyle I _ {\ tekst {L}} + I_ {0}$ :

${\ Displaystyle V = n V _ {\ tekst {T}} \ ln \ lewo ({\ Frac {I _ {\ tekst {L}} -I} {I_ {0}}} + 1 \ prawo) -IR_ {\ tekst {S}}.}$

W przeciwnym razie można rozwiązać dla V za pomocą funkcji Lamberta W:

${\ Displaystyle V = (I _ {\ tekst {L}} + I_ {0}) R _ {\ tekst {SH}} -I (R _ {\ tekst {S}} + R _ {\ tekst {SH}}) - nV_{\text{T}}W\left({\frac {I_{0}R_{\text{SH}}}{nV_{\text{T}}}}\exp \left({\frac {( I_{\text{L}}+I_{0}-I)R_{\text{SH}}}{nV_{\text{T}}}}\right)\right)}$

Jednak gdy RSH jest duże _, lepiej jest rozwiązać oryginalne równanie numerycznie.

Ogólną postacią rozwiązania jest krzywa, na której I maleje wraz ze wzrostem V (patrz wykresy poniżej). Nachylenie przy małym lub ujemnym V (gdzie funkcja W jest bliska zeru) zbliża się do ${\ Displaystyle -1 / (R _ {\ tekst {S}} + R _ {\ tekst {SH} })}$ , podczas gdy nachylenie przy wysokim V zbliża się do ${\ Displaystyle -1 / R _ {\ tekst {S}}}$ .

Napięcie jałowe i prąd zwarciowy

Gdy ogniwo pracuje w obwodzie otwartym , I = 0, a napięcie na zaciskach wyjściowych jest zdefiniowane jako napięcie obwodu otwartego . Zakładając, że rezystancja bocznika jest wystarczająco wysoka, aby pominąć końcowy wyraz równania charakterystycznego, napięcie obwodu otwartego V _OC wynosi:

${\ Displaystyle V _ {\ tekst {OC}} \ około {\ Frac {nkT} {q}} \ ln \ lewo ({\ Frac {I _ {\ tekst {L}}} {I_ {0}}} + 1 \Prawidłowy).}$

₀ Podobnie, gdy ogniwo pracuje w stanie zwarcia , V = 0, a prąd I płynący przez zaciski jest określany jako prąd zwarciowy . Można wykazać, że dla wysokiej jakości ogniwa słonecznego (niski R _S i I , a wysoki R _SH ) prąd zwarciowy I _SC wynosi:

${\ Displaystyle I _ {\ tekst {SC}} \ około I _ {\ tekst {L}}.}$

Nie jest możliwe pobranie zasilania z urządzenia podczas pracy w warunkach otwartego obwodu lub zwarcia.

Wpływ wielkości fizycznej

₀₀ Wartości I _L , I , RS _. i R _SH zależą od fizycznych rozmiarów ogniwa słonecznego Porównując skądinąd identyczne ogniwa, ogniwo z dwukrotnie większą powierzchnią złącza niż inne będzie w zasadzie miało dwukrotnie większe I L _i I , ponieważ ma dwukrotnie większy obszar, w którym generowany jest fotoprąd i przez który może przepływać prąd diody. Z tego _samego argumentu będzie miał również połowę RS rezystancji szeregowej związanej z pionowym przepływem prądu; jednak w przypadku wielkopowierzchniowych krzemowych ogniw słonecznych skalowanie rezystancji szeregowej napotykanej przez boczny przepływ prądu nie jest łatwe do przewidzenia, ponieważ będzie w dużej mierze zależeć od projektu sieci (nie jest jasne, co oznacza „poza tym identyczny” pod tym względem). W zależności od rodzaju bocznika, większa komórka może mieć również połowę RSH _, ponieważ ma dwa razy większy obszar, w którym mogą wystąpić boczniki; _z drugiej strony, jeśli boczniki występują głównie na obwodzie, wówczas RSH będzie się zmniejszać zgodnie ze zmianą obwodu, a nie powierzchni.

Ponieważ zmiany prądów są dominujące i wzajemnie się równoważą, napięcie jałowe jest praktycznie takie samo; VOC zaczyna zależeć od wielkości komórki tylko wtedy, gdy _RSH staje _się zbyt niskie. Aby uwzględnić dominację prądów, równanie charakterystyczne jest często zapisywane w kategoriach gęstości prądu lub prądu wytwarzanego na powierzchnię komórki elementarnej:

${\ Displaystyle J = J _ {\ tekst {L}} -J_ {0 }\left\{\exp \left[{\frac {q(V+Jr_{\text{S}})}{nkT}}\right]-1\right\}-{\frac {V+Jr_{ \text{S}}}{r_{\text{SH}}}}}$

Gdzie

• J , gęstość prądu (amper/cm ² )
• J _L , gęstość prądu fotogenerowanego (amper/cm ² )
• ₀ J , gęstość prądu nasycenia wstecznego (amper/cm ² )
• r _S , właściwa rezystancja szeregowa (Ω·cm ² )
• r _SH , właściwa rezystancja bocznika (Ω·cm ² ).

Ten preparat ma kilka zalet. Jednym z nich jest to, że ponieważ charakterystyki komórek odnoszą się do wspólnego pola przekroju poprzecznego, można je porównywać dla komórek o różnych wymiarach fizycznych. Chociaż przynosi to ograniczone korzyści w warunkach produkcyjnych, gdzie wszystkie ogniwa mają zwykle ten sam rozmiar, jest przydatne w badaniach i porównywaniu ogniw różnych producentów. Kolejną zaletą jest to, że równanie gęstości w naturalny sposób skaluje wartości parametrów do podobnych rzędów wielkości, co może sprawić, że ich ekstrakcja numeryczna będzie prostsza i dokładniejsza, nawet przy użyciu naiwnych metod rozwiązywania.

₀ Istnieją praktyczne ograniczenia tego preparatu. Na przykład niektóre efekty pasożytnicze zyskują na znaczeniu w miarę zmniejszania się rozmiarów komórek i mogą wpływać na wartości wyodrębnionych parametrów. Rekombinacja i zanieczyszczenie połączenia są zwykle największe na obwodzie komórki, więc bardzo małe komórki mogą wykazywać wyższe wartości J lub niższe wartości RSH niż większe komórki, które poza tym są identyczne _. W takich przypadkach porównań między komórkami należy dokonywać ostrożnie i mając na uwadze te efekty.

Takie podejście powinno być stosowane wyłącznie do porównywania ogniw słonecznych o porównywalnym układzie. Na przykład porównanie między zasadniczo kwadratowymi ogniwami słonecznymi, takimi jak typowe ogniwa słoneczne z krzemu krystalicznego, a wąskimi, ale długimi ogniwami słonecznymi, takimi jak typowe cienkowarstwowe ogniwa słoneczne, może prowadzić do błędnych założeń spowodowanych różnymi rodzajami ścieżek prądowych, a zatem wpływem na przykład rozproszony wkład rezystancji szeregowej do r _S . Makroarchitektura ogniw słonecznych może skutkować umieszczeniem różnych obszarów powierzchni w dowolnej ustalonej objętości - szczególnie w przypadku cienkowarstwowych ogniw słonecznych i elastyczne ogniwa słoneczne, które mogą pozwolić na wysoce zawiłe złożone struktury. Jeśli wiążącym ograniczeniem jest objętość, gęstość wydajności oparta na polu powierzchni może mieć mniejsze znaczenie.

Przezroczyste elektrody przewodzące

Schemat pobierania ładunku przez elektrody ogniw słonecznych. Światło przechodzi przez przezroczystą elektrodę przewodzącą, tworząc pary dziur elektronowych, które są zbierane przez obie elektrody.

Przezroczyste elektrody przewodzące są niezbędnymi składnikami ogniw słonecznych. Jest to albo ciągła warstwa tlenku cyny indu , albo przewodząca sieć drutów, w której druty są kolektorami ładunku, podczas gdy puste przestrzenie między drutami są przezroczyste dla światła. Optymalna gęstość sieci przewodów jest niezbędna dla maksymalnej wydajności ogniwa słonecznego, ponieważ wyższa gęstość drutu blokuje przepuszczalność światła, podczas gdy niższa gęstość drutu prowadzi do dużych strat rekombinacyjnych z powodu większej odległości przebytej przez nośniki ładunku.

Temperatura ogniwa

Wpływ temperatury na charakterystykę prądowo-napięciową ogniwa słonecznego

₀₀ Temperatura wpływa na charakterystyczne równanie na dwa sposoby: bezpośrednio, poprzez T w wyrażeniu wykładniczym, i pośrednio, poprzez wpływ na I (ściśle mówiąc, temperatura wpływa na wszystkie składniki, ale te dwa znacznie bardziej niż pozostałe). Podczas gdy zwiększanie T zmniejsza wielkość wykładnika w równaniu charakterystycznym, wartość I rośnie wykładniczo wraz z T . Efektem netto jest zmniejszenie V _OC (napięcie obwodu otwartego) liniowo ze wzrostem temperatury. Wielkość tej redukcji jest odwrotnie proporcjonalna _do VOC ; to znaczy ogniwa o wyższych wartościach V _OC ulegają mniejszym spadkom napięcia wraz ze wzrostem temperatury. W przypadku większości ogniw słonecznych z krzemu krystalicznego zmiana V _OC wraz z temperaturą wynosi około -0,50%/°C, chociaż wskaźnik dla ogniw z krzemu krystalicznego o najwyższej wydajności wynosi około -0,35%/°C. Dla porównania, współczynnik dla ogniw słonecznych z amorficznego krzemu wynosi od -0,20 do -0,30%/°C, w zależności od tego, jak wykonane jest ogniwo.

Ilość fotogenerowanego prądu I _L nieznacznie wzrasta wraz ze wzrostem temperatury z powodu wzrostu liczby termicznie generowanych nośników w ogniwie. Efekt ten jest jednak niewielki: około 0,065%/°C dla ogniw z krzemu krystalicznego i 0,09% dla ogniw z krzemu amorficznego.

Ogólny wpływ temperatury na wydajność ogniwa można obliczyć za pomocą tych współczynników w połączeniu z równaniem charakterystycznym. Ponieważ jednak zmiana napięcia jest znacznie silniejsza niż zmiana prądu, ogólny wpływ na wydajność jest zwykle podobny do wpływu na napięcie. Wydajność większości krystalicznych krzemowych ogniw słonecznych spada o 0,50%/°C, a większości ogniw amorficznych o 0,15-0,25%/°C. Powyższy rysunek przedstawia krzywe IV, które zwykle można zaobserwować dla ogniwa słonecznego z krystalicznego krzemu w różnych temperaturach.

Odporność szeregowa

Wpływ rezystancji szeregowej na charakterystykę prądowo-napięciową ogniwa słonecznego

Wraz ze wzrostem rezystancji szeregowej spadek napięcia między napięciem złącza a napięciem na zaciskach staje się większy dla tego samego prądu. W rezultacie sterowana prądem część krzywej IV zaczyna opadać w kierunku początku, powodując znaczny spadek napięcia na zaciskach _V i nieznaczne zmniejszenie ISC , prądu zwarciowego. Bardzo wysokie wartości R _S również spowodują znaczną redukcję I _SC ; w tych reżimach dominuje rezystancja szeregowa, a zachowanie ogniwa słonecznego przypomina zachowanie rezystora. Efekty te są pokazane dla ogniw słonecznych z krzemu krystalicznego na krzywych IV przedstawionych na rysunku po prawej stronie.

Straty spowodowane rezystancją szeregową są w pierwszym przybliżeniu podane jako P _strata = V _Rs I = I ² R _S i rosną kwadratowo wraz z (foto)prądem. Straty rezystancji szeregowej są zatem najważniejsze przy wysokich natężeniach oświetlenia.

Rezystancja bocznika

Wpływ rezystancji bocznikowej na charakterystykę prądowo-napięciową ogniwa słonecznego

Gdy rezystancja bocznika maleje, prąd przepływający przez rezystor bocznikowy wzrasta dla danego poziomu napięcia złącza. W rezultacie sterowana napięciem część krzywej IV zaczyna opadać daleko od początku, powodując znaczny spadek prądu końcowego _I i nieznaczne zmniejszenie VOC . _Bardzo niskie wartości RSH spowodują znaczną redukcję V _OC . Podobnie jak w przypadku dużej rezystancji szeregowej, źle zbocznikowane ogniwo słoneczne będzie miało charakterystykę działania zbliżoną do rezystora. Efekty te są pokazane dla ogniw słonecznych z krzemu krystalicznego na krzywych IV przedstawionych na rysunku po prawej stronie.

Odwrotny prąd nasycenia

Wpływ wstecznego prądu nasycenia na charakterystykę prądowo-napięciową ogniwa słonecznego

Zakładając nieskończoną rezystancję bocznika, można rozwiązać równanie charakterystyczne dla V _OC :

${\ Displaystyle V _ {\ tekst {OC}} = {\ Frac {kT} {q}} \ ln \ lewo ({\ Frac {I_ {\ tekst {SC}}} {I_ {0}}} + 1 \ Prawidłowy).}$

_{0 Zatem} wzrost I powoduje zmniejszenie VOC proporcjonalne do odwrotności logarytmu wzrostu. Wyjaśnia to matematycznie przyczynę redukcji V _OC , która towarzyszy opisanemu powyżej wzrostowi temperatury. Wpływ odwrotnego prądu nasycenia na krzywą IV krystalicznego krzemowego ogniwa słonecznego pokazano na rysunku po prawej stronie. Fizycznie prąd nasycenia wstecznego jest miarą „wycieku” nośników przez złącze pn w polaryzacji zawrotnej. Ten wyciek jest wynikiem rekombinacji nośników w obszarach neutralnych po obu stronach złącza.

Czynnik idealności

Wpływ współczynnika idealności na charakterystykę prądowo-napięciową ogniwa słonecznego

Współczynnik idealności (zwany także współczynnikiem emisyjności) to parametr dopasowania, który opisuje, jak bardzo zachowanie diody odpowiada zachowaniu przewidywanemu przez teorię, która zakłada, że ​​złącze pn diody jest płaszczyzną nieskończoną i że w obszarze ładunku przestrzennego nie zachodzi żadna rekombinacja. Idealne dopasowanie do teorii jest wskazane, gdy n = 1 . Jednak gdy rekombinacja w obszarze ładunku przestrzennego dominuje nad inną rekombinacją, n = 2 . Efekt zmiany współczynnika idealności niezależnie od wszystkich innych parametrów jest pokazany dla ogniwa słonecznego z krzemu krystalicznego na krzywych IV przedstawionych na rysunku po prawej stronie.

₀ Większość ogniw słonecznych, które są dość duże w porównaniu z konwencjonalnymi diodami, dobrze zbliża się do nieskończonej płaszczyzny i zazwyczaj wykazuje prawie idealne zachowanie w standardowych warunkach testowych ( n ≈ 1 ). Jednak w pewnych warunkach pracy działanie urządzenia może być zdominowane przez rekombinację w obszarze ładunku kosmicznego. Charakteryzuje się to znacznym wzrostem I oraz wzrostem współczynnika idealności do n ≈ 2 ₀₀ . Ten ostatni ma tendencję do zwiększania napięcia wyjściowego ogniwa słonecznego, podczas gdy ten pierwszy powoduje jego erozję. Efekt netto jest zatem kombinacją wzrostu napięcia pokazanego przy wzroście n na rysunku po prawej i spadku napięcia pokazanego przy wzroście I na powyższym rysunku. Zazwyczaj I jest bardziej znaczącym czynnikiem, a wynikiem jest obniżenie napięcia.

Czasami obserwuje się, że współczynnik idealności jest większy niż 2, co generalnie przypisuje się obecności diody Schottky'ego lub heterozłącza w ogniwie słonecznym. Obecność przesunięcia heterozłącza zmniejsza wydajność zbierania ogniwa słonecznego i może przyczynić się do niskiego współczynnika wypełnienia.

Zobacz też

• Siła elektromotoryczna § Ogniwo słoneczne

Linki zewnętrzne

• Kalkulator równoważnego obwodu latarni morskiej PV
• Objaśnienie chemii — ogniwa słoneczne z Chemicalexplained.com