Właściwość rozszerzenia homotopii

W matematyce , w obszarze topologii algebraicznej , właściwość rozszerzenia homotopii wskazuje, które homotopie zdefiniowane w podprzestrzeni można rozszerzyć do homotopii zdefiniowanej w większej przestrzeni. Właściwość rozciągania homotopii kofibracji jest podwójna w stosunku do właściwości podnoszenia homotopii , która jest używana do definiowania włókien .

Definicja

Niech $i$ będzie przestrzenią topologiczną niech ${\ Displaystyle A \ podzbiór X}$ . Mówimy $\ dwukropek A\rightarrow Y^{I}}$ że para ma właściwość rozszerzenia homotopii , jeśli biorąc pod uwagę homotopię $∙$ i mapa ${\ Displaystyle {\ tylda {f}} _ {0} \ dwukropek X \ rightarrow Y}$ takie, że

$${\ Displaystyle {\ tylda {f}} _ {0} \ circ \ jota = \ lewo. {\ tylda {f}} _ {0} \ prawo | _ {A} = f_{0}=\pi _{0}\circ f_{\punktor},}$$

wtedy istnieje rozszerzenie do homotopii ${\ Displaystyle f _ {\ punktor}}$ do homotopii ${\ Displaystyle {\ tylda {f}} _ {\ punktor} \ dwukropek X \ rightarrow Y ^ {I}}$ takie, że ${\ Displaystyle {\ tylda {f}} _ {\ punktor} \ circ \ jota = \ lewo. {\ tylda {f}} _ {\ punktor} \ prawo | _ {A} = f_ {\ punktor }}$ .

$mapa$ że para homotopii, jeśli $X$ można rozszerzyć do mapy $zgadzają się co$$\ rightarrow Y}$ (tj $.$ i ich wspólnej domeny).

$!}$ właściwość tylko dla określonej domeny kodowej , mówimy, że ma właściwość rozszerzenia homotopii w odniesieniu do $Displaystyle Y \$ do ${\ Displaystyle Y \, \!}$ .

Wyobrażanie sobie

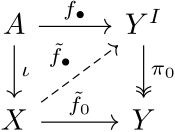
Właściwość rozszerzenia homotopii jest przedstawiona na poniższym diagramie

Jeśli powyższy diagram (bez mapy przerywanej) komutuje (jest to równoważne powyższym warunkom), to para (X, A) ma właściwość rozszerzenia homotopii, jeśli istnieje mapa fa ~ ∙ {\ displaystyle {\ $} }_{\bullet }}$ co sprawia, że ​​diagram jest komutowany. Curry $as$ że homotopie jako są w mapy ${\ Displaystyle {\ tylda {f}} _ {\ punktor} \ dwukropek X \ razy I \ do Y}$ .

Zauważ, że ten diagram jest podwójny (przeciwny do) diagramu właściwości podnoszenia homotopii ; ta dwoistość jest luźno nazywana dualnością Eckmanna-Hiltona .

Nieruchomości

• Jeśli $\ Displaystyle X \, \!}$${\ Displaystyle X \, \!}$ Jest kompleksem komórkowym i jest podkompleksem $,$ to para ${ \displaystyle (X,A)\,\!}$ ma właściwość rozszerzenia homotopii.
• Para ${\ Displaystyle (X, A) \, \!}$ Ma właściwość rozszerzenia homotopii wtedy i tylko wtedy, gdy ${\ Displaystyle (X \ razy \ {0 \ }\cup A\times I)$${\ Displaystyle X \ razy I.}$ jest wycofaniem X

Inny

Jeśli $, A)}$${$ \ Displaystyle ( właściwość rozszerzenia homotopii, to prosta mapa kofibracją

W rzeczywistości $ze$ jeśli weźmiesz pod uwagę jakąkolwiek $to$ , mamy, że pod ${\ Displaystyle \ jota}$ . Oznacza to, że dowolne kofibracje można traktować jako mapę inkluzyjną, a zatem można je traktować jako posiadające właściwość rozszerzenia homotopii.

Zobacz też

• Właściwość podnoszenia homotopii

•   Hatcher, Allen (2002). Topologia algebraiczna . Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-79540-0 .
• „Właściwość rozszerzenia homotopii” . Planeta Matematyka .