Wahadło kwantowe

Wahadło kwantowe ma fundamentalne znaczenie dla zrozumienia wewnętrznych rotacji z przeszkodą w chemii, kwantowych cech rozpraszania atomów, a także wielu innych zjawisk kwantowych. Chociaż wahadło nie podlegające aproksymacji małych kątów ma nieodłączną nieliniowość, równanie Schrödingera dla skwantowanego układu można stosunkowo łatwo rozwiązać.

Równanie Schrödingera

Korzystając z mechaniki Lagrange'a z mechaniki klasycznej, można opracować hamiltonian dla systemu. Proste wahadło $ma$ jedną uogólnioną współrzędną (przemieszczenie kątowe i dwa ograniczenia (długość struny i płaszczyznę ruchu). Można znaleźć energie kinetyczną i potencjalną układu

$\ Displaystyle T = {\ Frac {1} {2}} ml ^ {2} {\ kropka {\ phi}} ^ {2},}$

${\ Displaystyle U = mgl (1- \ cos \ phi).}$

Prowadzi to do hamiltonianu

${\ Displaystyle {\ kapelusz {H}} = {\ Frac {{\ kapelusz {p}} ^ {2}} {2 ml ^ {2}}} + mgl (1- \ cos \ fi).}$

Zależne od czasu równanie Schrödingera dla systemu to

${\ Displaystyle i \ hbar {\ Frac {d \ psi} {dt}} = - {\ frac {\ hbar ^ {2}} {2 ml ^ {2}}} {\ frac {d ^ {2} \ psi }{d\phi ^{2}}}+mgl(1-\cos \phi )\Psi .}$

Należy rozwiązać niezależne od czasu równanie Schrödingera, aby znaleźć poziomy energii i odpowiadające im stany własne. Najlepiej to osiągnąć, zmieniając zmienną niezależną w następujący sposób:

${\ Displaystyle \ eta = \ phi + \ pi,}$

${\ Displaystyle \ Psi = \ psi e ^ {-iEt / \ hbar},}$

${\ Displaystyle E \ psi = - {\ Frac {\ hbar ^ {2}} {2 ml ^ {2}}} {\ Frac {d ^ {2} \ psi }{ d \ eta ^ {2}}} + mgl(1+\cos \eta )\psi .}$

To jest po prostu równanie różniczkowe Mathieu

${\ Displaystyle {\ Frac {d ^ { 2}\psi }{d\eta ^{2}}}+\left({\frac {2mEl^{2}}{\hbar ^{2}}}-{\frac {2m^{2}gl^ {3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi =0, }$

których rozwiązaniami są funkcje Mathieu .

Rozwiązania

Energie

Biorąc pod uwagę $okresem$$policzalnie$ wielu wartości specjalnych $wartościami$ zwanych charakterystycznymi , równanie Mathieu dopuszcza rozwiązania, które są okresowe . Za ${\ Displaystyle a_ {n} (q), b_ {n} (q)}$ gdzie ${\ displaystyle n}$ jest liczbą naturalną . Okresowe przypadki specjalne funkcji cosinus i sinus Mathieu są często zapisywane ${\ Displaystyle CE (n, q, x), SE (n, q , x)}$ odpowiednio, chociaż tradycyjnie podaje się im inną normalizację (mianowicie, że ich norma jest równa ${\ displaystyle L ^ {2}}$${\ displaystyle \ pi}$ ).

Warunki brzegowe w wahadle kwantowym implikują, że $są$ następujące dla danego za $}$$\ Displaystyle a_ {n} (q), b_ {n} (q)$ :

${\ Displaystyle {\ Frac {d ^ {2} \ psi } {d \ eta ^ {2}}} + \ lewo ({\ Frac {2mEl ^ {2}} {\ hbar ^ {2}}} - { \frac {2m^{2}gl^{3}}{\hbar ^{2}}}-{\frac {2m^{2}gl^{3}}{\hbar ^{2}}}\cos \eta \right)\psi = 0,}$

${\ Displaystyle a_ {n} (q), b_ {n} (q) = {\ Frac {2mEl ^ {2}} {\ hbar ^ {2}}} - {\ Frac {2m ^ {2} gl ^ {3}}{\hbar ^{2}}}.}$

Energie układu ${\ Displaystyle E = mgl + {\ Frac {\ hbar ^ {2} a_ {n} ( q),b_{n}(q)}{2ml^{2}}}}$ odpowiednio dla rozwiązań parzystych/nieparzystych są kwantowane na podstawie wartości charakterystycznych znalezionych przez rozwiązanie równania Mathieu.

Efektywną potencjalną głębokość można zdefiniować jako

${\ Displaystyle q = {\ Frac {m ^ {2} gl ^ {3}} {\ hbar ^ {2}}}.}$

Głęboki potencjał daje dynamikę cząstki w niezależnym potencjale. Natomiast w płytkim potencjale znaczenie mają fale Blocha , a także tunelowanie kwantowe .

Ogólne rozwiązanie

Ogólnym rozwiązaniem powyższego równania różniczkowego dla danej wartości a i q jest zbiorem liniowo niezależnych cosinusów Mathieu i sinusów Mathieu, które są odpowiednio rozwiązaniami parzystymi i nieparzystymi. Ogólnie funkcje Mathieu są aperiodyczne; jednak dla charakterystycznych wartości cosinus i sinus Mathieu stają się okresowe z okresem ${\ Displaystyle 2 \ pi}$${\ Displaystyle a_ {n} (q), b_ {n} (q)$ .

Stany własne

Dla dodatnich wartości q prawdziwe jest:

${\ Displaystyle C (a_ {n} (q), q, x) = { \frac {CE(n,q,x)}{CE(n,q,0)}},}$

${\ Displaystyle S (b_ {n} (q), q, x) = {\ Frac {SE (n, q, x)} {SE' (n, q, 0)}}.}$

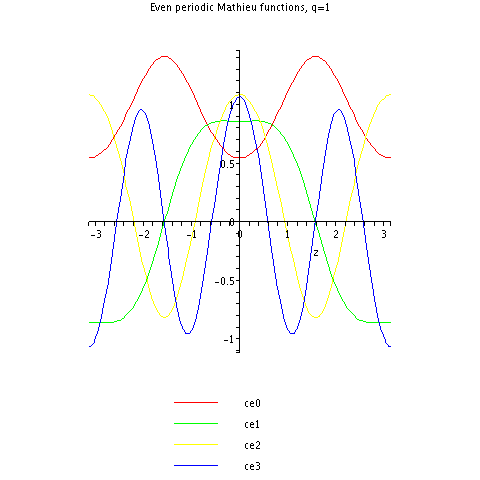
Oto kilka pierwszych okresowych funkcji kosinusowych Mathieu dla ${\ displaystyle q = 1}$ .

$wzgórzami$ , że na przykład (zielony) przypomina funkcję cosinus,

Zobacz też

• Kwantowy oscylator harmoniczny

Bibliografia

•   Bransden, BH; Joachain, CJ (2000). Mechanika kwantowa (wyd. 2). Essex: Edukacja Pearson. ISBN 0-582-35691-1 .
•   Davies, John H. (2006). Fizyka półprzewodników niskowymiarowych: wprowadzenie (wyd. 6 przedruk). Wydawnictwo Uniwersytetu Cambridge. ISBN 0-521-48491-X .
•   Griffiths, David J. (2004). Wprowadzenie do mechaniki kwantowej (wyd. 2). Sala Prentice'a. ISBN 0-13-111892-7 .
• Muhammad Ayub, Atom Optics Quantum Pendulum , 2011, Islamabad, Pakistan, https://arxiv.org/abs/1012.6011