Widmowe grupowanie

Przykładowy spójny graf z 6 wierzchołkami.

Podział na dwa połączone grafy

W statystyce wielowymiarowej techniki grupowania widmowego wykorzystują widmo ( wartości własne ) macierzy podobieństwa danych do przeprowadzenia redukcji wymiarowości przed grupowaniem w mniejszej liczbie wymiarów. Macierz podobieństw jest dostarczana jako dane wejściowe i składa się z ilościowej oceny względnego podobieństwa każdej pary punktów w zbiorze danych.

W zastosowaniu do segmentacji obrazu grupowanie widmowe jest znane jako kategoryzacja obiektów oparta na segmentacji .

Definicje

Biorąc pod uwagę wyliczony zestaw punktów danych, macierz podobieństwa można zdefiniować jako macierz symetryczną , gdzie $A_ {ij} \ geq 0}$$Displaystyle$ reprezentuje miarę podobieństwa między punktami danych ZA {\ displaystyle A z indeksami $displaystyle j}$$\$ { . Ogólne podejście do grupowania widmowego polega na użyciu standardowej grupowania (istnieje wiele takich metod, k -średnie omówiono poniżej $.$ na odpowiednich wektorach własnych macierzy Laplace'a Istnieje wiele różnych sposobów definiowania Laplace'a, które mają różne interpretacje matematyczne, więc grupowanie będzie również miało różne interpretacje. Istotne wektory własne to te, które odpowiadają najmniejszym kilku wartościom własnym Laplace'a, z wyjątkiem najmniejszej wartości własnej, która będzie miała wartość 0. Dla wydajności obliczeniowej te wektory własne są często obliczane jako wektory własne odpowiadające kilku największym wartościom własnym a funkcja Laplace'a.

Macierz Laplace'a

Dwuwymiarowy system sprężyn.

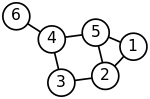
Widmowe grupowanie jest dobrze znane jako związane z podziałem układu masa-sprężyna, gdzie każda masa jest powiązana z punktem danych, a każda sztywność sprężyny odpowiada wadze krawędzi opisującej podobieństwo dwóch powiązanych punktów danych, jak na wiosnę system . W szczególności odniesienie klasyczne wyjaśnia, że ​​​​problem wartości własnej opisujący mody drgań poprzecznych układu masa-sprężyna jest dokładnie taki sam, jak problem wartości własnej dla wykresu macierzy Laplaca zdefiniowanej jako

${\ Displaystyle L: = DA}$ ,

gdzie jest $macierzą$ _

${\ Displaystyle D_ {ii} = \ suma _ {j} A_ {ij},}$

a A jest macierzą sąsiedztwa .

Masy, które są ściśle połączone sprężynami w układzie masa-sprężyna, najwyraźniej poruszają się razem z położenia równowagi w modach drgań o niskiej częstotliwości, tak że składowe wektorów własnych odpowiadające najmniejszym wartościom własnym grafu Laplaciana mogą być użyte do sensownego skupienie mas. Na przykład, zakładając, że wszystkie sprężyny i masy są identyczne w pokazanym dwuwymiarowym układzie sprężyn, można by intuicyjnie oczekiwać, że najluźniejsze połączone masy po prawej stronie układu poruszałyby się z największą amplitudą i odwrotnie kierunku do reszty mas, gdy układ jest wstrząśnięty — a oczekiwanie to zostanie potwierdzone analizując składowe wektorów własnych grafu Laplace'a odpowiadające najmniejszym wartościom własnym, czyli najmniejszym częstotliwości drgań .

Normalizacja macierzy Laplaca

Celem normalizacji jest sprawienie, aby wszystkie przekątne wpisów macierzy Laplace'a były jednostkami, a także odpowiednie skalowanie wpisów poza przekątną. W grafie ważonym wierzchołek może mieć duży stopień ze względu na małą liczbę połączonych krawędzi, ale przy dużych wagach równie dobrze ze względu na dużą liczbę połączonych krawędzi o jednostkowych wagach.

Popularną techniką znormalizowanego grupowania widmowego jest algorytm znormalizowanych cięć lub algorytm Shi-Malik wprowadzony przez Jianbo Shi i Jitendra Malika , powszechnie używany do segmentacji obrazu . Dzieli punkty na dwa zbiory na podstawie $Displaystyle$ własnego odpowiadającego drugiej najmniejszej wartości własnej symetrycznego znormalizowanego Laplace'a $(B_ {1}, B_ {2})}$ zdefiniowana jako

${\ Displaystyle L ^ {\ tekst {norma}}: = ID ^ {-1/2} AD ^ {-1/2}.}$

Wektor jest również wektorem własnym odpowiadającym drugiej co do wielkości wartości własnej symetrycznie ${\ Displaystyle D ^ {-1/2} AD ^ {-1/2}.}$ macierzy $/$

Błąd losowy (lub lewy) znormalizowany Laplace'a jest zdefiniowany jako

${\ Displaystyle L ^ {\ tekst {rw}}: = D ^ {- 1} L = ID ^ {- 1} A}$

i może być również używany do grupowania widmowego. Matematycznie $_$$sąsiedztwa$ własny największej wartości własnej macierzy błądzenia losowego

Wektor własny $znormalizowanego$ laplace'a i wektor własny $znormalizowanego$ laplace'a są powiązane tożsamością ${\ Displaystyle D ^ {-1/2} v = u.}$

Analiza klastrów poprzez Spectral Embedding

Znając $mapowanie - zwane osadzeniem widmowym$ wybranych wektorów własnych, - oryginalnych punktów $danych$$n}$$displaystyle$ na ${\ displaystyle k}$ -wymiarowa przestrzeń wektorowa przy użyciu rzędów ${\ displaystyle V}$ . Teraz analiza ogranicza się do grupowania wektorów ze $składnikami$ , co można zrobić na różne sposoby

W najprostszym przypadku $wybrany$ pojedynczy wektor własny $wektorem$ zwany Fiedlera odpowiada drugiej najmniejszej wartości Używając składowych można umieścić wszystkie punkty, których składowa w $B_{-}}$$dodatnia$$w$${$ a resztę w zbiorze $+}}$ , dzieląc w ten sposób wykres na dwie części i oznaczając punkty danych dwiema etykietami. To podejście oparte na znakach jest zgodne z intuicyjnym wyjaśnieniem klastrowania widmowego za pomocą modelu masa-sprężyna - w trybie wibracji o niskiej częstotliwości, który wektor Fiedlera , jeden punkt danych klastra zidentyfikowany ze wzajemnie silnie połączonymi masami poruszałby się razem v {\ $v}$ w jednym kierunku, podczas gdy w klastrze dopełniającym punkty danych utożsamiane z pozostałymi masami poruszałyby się razem w przeciwnym kierunku. Algorytm może być używany do hierarchicznego klastrowania przez wielokrotne partycjonowanie podzbiorów w ten sam sposób.

W ogólnym przypadku można zastosować dowolną technikę grupowania wektorów $,$ .

Algorytmy

Podstawowy algorytm

1. Oblicz Laplace'a (lub znormalizowanego Laplace'a) ${\ displaystyle L}$
2. $k$ pierwsze $własne$ (wektory własne odpowiadające najmniejszym wartościom własnym ) $displaystyle$ }
3. Rozważ macierz utworzoną przez pierwsze $własne$ ; l ${\ displaystyle l}$ -ty wiersz określa cechy węzła wykresu $\ displaystyle l}$
4. Pogrupuj węzły wykresu w oparciu o te cechy (np. używając grupowania k-średnich )

Jeśli macierz podobieństwa $}$ została jeszcze jawnie skonstruowana, wydajność grupowania widmowego można poprawić, jeśli rozwiązanie odpowiedniego problemu wartości własnej zostanie przeprowadzone w sposób wolny od macierzy (bez jawnego manipulowania lub nawet obliczania podobieństwa ZA {\ displaystyle A macierz), jak w algorytmie Lanczosa .

W przypadku grafów o dużych rozmiarach druga wartość własna (znormalizowanej) macierzy Laplace'a wykresu jest często źle uwarunkowana , co prowadzi do powolnej zbieżności iteracyjnych solwerów wartości własnych. Kluczową technologią przyspieszającą konwergencję jest kondycjonowanie wstępne , np. w bezmatrycowej metodzie LOBPCG . Grupowanie widmowe zostało z powodzeniem zastosowane na dużych grafach, najpierw identyfikując ich strukturę społeczności , a następnie grupując społeczności.

Grupowanie widmowe jest ściśle związane z nieliniową redukcją wymiarowości , a techniki redukcji wymiarów, takie jak osadzanie lokalnie liniowe, mogą być stosowane w celu zmniejszenia błędów spowodowanych szumem lub wartościami odstającymi.

Koszty

Oznaczając liczbę punktów danych $jako$ ważne jest, aby oszacować wielkość pamięci i czas obliczeń lub liczbę wykonanych operacji arytmetycznych (AO $)$ . Bez względu na algorytm grupowania widmowego, dwoma głównymi $kosztownymi$ elementami są konstrukcja wykresu Laplace'a i określenie jego własnych dla osadzania widmowego. Ostatni krok - określenie etykiet na podstawie ${\ displaystyle n}$ -by- ${\ displaystyle k}$$AO$$.$ jest zazwyczaj najtańszą, wymagającą tylko $wektora$ tylko etykiet w pamięci

Konieczność skonstruowania grafu Laplace'a jest wspólna dla wszystkich metod grupowania opartych na odległości lub korelacji. Obliczanie wektorów własnych jest specyficzne tylko dla grupowania widmowego.

Konstruowanie grafu Laplace'a

Graf Laplace'a może być i zwykle jest zbudowany z macierzy sąsiedztwa. Konstrukcję można przeprowadzić bez macierzy, tj. bez jawnego tworzenia macierzy grafu Laplace'a i bez AO. Można to również wykonać zamiast macierzy sąsiedztwa bez zwiększania zużycia pamięci. Tak czy inaczej, koszt skonstruowania wykresu Laplace'a jest zasadniczo określony przez koszty skonstruowania macierzy sąsiedztwa wykresu ${\ displaystyle n}$ -by- ${\ displaystyle n}$

Co więcej, znormalizowany Laplacian ma dokładnie takie same wektory własne jak znormalizowana macierz sąsiedztwa, ale z odwróconą kolejnością wartości własnych. Zatem zamiast obliczać wektory własne odpowiadające najmniejszym wartościom własnym znormalizowanego Laplaciana, można równoważnie obliczyć wektory własne odpowiadające największym wartościom własnym znormalizowanej macierzy sąsiedztwa, nawet nie mówiąc o macierzy Laplaca.

Naiwne konstrukcje macierzy sąsiedztwa grafu , np. Przy użyciu jądra RBF, sprawiają, że jest ona gęsta, co wymaga $n ^ {2}}$ AO do określenia każdego z $displaystyle$ wpisy macierzy. ${\ displaystyle n ^ {2}}$ Metodę Nystroma można wykorzystać do aproksymacji macierzy podobieństwa, ale aproksymowana macierz nie jest elementarnie dodatnia, tj. nie może być interpretowana jako podobieństwo oparte na odległości.

Algorytmy konstruowania macierzy sąsiedztwa wykresu jako macierzy rzadkiej są zwykle oparte na wyszukiwaniu najbliższego sąsiada , które szacuje lub próbkuje sąsiedztwo danego punktu danych dla najbliższych sąsiadów i oblicza niezerowe wpisy macierzy sąsiedztwa, porównując tylko pary sąsiedzi. Liczba wybranych najbliższych sąsiadów określa zatem liczbę niezerowych wpisów i często jest ustalana tak, że ślad $wynosi$$macierzy$ sąsiedztwa tylko ${\ Displaystyle O (n)}$$Displaystyle$ sekwencyjne operacje arytmetyczne są potrzebne do obliczenia niezerowych wpisów, a $(n)}$ obliczenia można trywialnie wykonywać równolegle.

Obliczanie wektorów własnych

Koszt obliczenia macierzy wybranych wektorów własnych wykresu Laplace'a jest zwykle $\ Displaystyle k \ ll n$ do kosztu mnożenia $}$${$ - przez - k {\ Displaystyle k n ${\ displaystyle n}$ -by- ${\ displaystyle n} wykresu macierzy Laplace'a przez wektor,$ różni się znacznie, czy macierz Laplaca jest gęsta czy rzadka. Dla gęstego przypadku koszt wynosi zatem ${\ Displaystyle O (n ^ {2})}$ . $cytowany$ w literaturze koszt $ponieważ$ wyboru np. W grupowanie widmowe określone przez wektor Fiedlera ${\ displaystyle k = 1}$ .

nielicznym przypadku wykresu macierzy Laplace'a z $niezerowymi$$Displaystyle$ , koszt iloczynu macierzowo-wektorowego $(n)}$ a zatem obliczenie macierzy wybranych wektorów własnych $Displaystyle$$k \ ll n} -$$przez - k {$ Displaystyle } jest ${\ Displaystyle O (n)}$$są$$zajętości$ pamięci również tylko optymalnymi dolnymi granicami złożoności danych Co więcej, bezmacierzowe solwery wartości własnych, takie jak LOBPCG , mogą wydajnie działać równolegle, np. na wielu procesorach graficznych z rozproszoną pamięcią, co skutkuje nie tylko wysokiej jakości klastrami, z których słynie klastrowanie widmowe, ale także najwyższą wydajnością.

Oprogramowanie

Darmowe oprogramowanie implementujące grupowanie widmowe jest dostępne w dużych projektach open source, takich jak scikit-learn przy użyciu LOBPCG z wielosiatkowym uwarunkowaniem wstępnym lub ARPACK , MLlib do klastrowania pseudowektorów własnych przy użyciu metody iteracji mocy i R .

Związek z innymi metodami grupowania

Idee stojące za grupowaniem widmowym mogą nie być od razu oczywiste. Przydatne może być podkreślenie relacji z innymi metodami. W szczególności można to opisać w kontekście metod grupowania jądra, które ujawniają kilka podobieństw z innymi podejściami.

Związek z k -średnimi

Ważony problem k -średnich jąder dzieli funkcję celu z problemem grupowania widmowego, który można optymalizować bezpośrednio metodami wielopoziomowymi.

Związek z DBSCAN

W trywialnym przypadku określania połączonych elementów grafu — optymalnych klastrów bez odciętych krawędzi — grupowanie widmowe jest również powiązane z widmową wersją klastrowania DBSCAN , która znajduje komponenty połączone gęstością.

Miary porównywania klastrów

Ravi Kannan, Santosh Vempala i Adrian Vetta zaproponowali miarę dwukryterialną w celu zdefiniowania jakości danego skupienia. Powiedzieli, że skupienie jest skupieniem (α, ε), jeśli przewodnictwo każdego skupienia (w skupieniu) wynosi co najmniej α, a masa krawędzi między skupieniami wynosi co najwyżej ε ułamka całkowitej masy wszystkich krawędzie w grafie. Przyglądają się również dwóm algorytmom aproksymacji w tym samym artykule.

Literatura historyczna i pokrewna

Klastrowanie widmowe ma długą historię. Grupowanie widmowe jako uczenia maszynowego zostało spopularyzowane przez Shi i Malik oraz Ng, Jordan i Weiss.

Pomysły i środki sieciowe związane z klastrowaniem widmowym również odgrywają ważną rolę w wielu zastosowaniach pozornie różniących się od problemów związanych z klastrowaniem. Na przykład sieci z silniejszymi podziałami widmowymi potrzebują więcej czasu na zbieżność w aktualizujących opinie modelach stosowanych w socjologii i ekonomii.

Zobacz też

• Propagacja powinowactwa
• Analiza głównych składników jądra
• Analiza skupień
• Teoria grafów widmowych