Wstrząs dziobowy (aerodynamika)
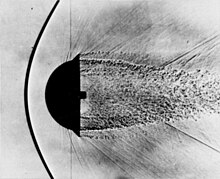
Wstrząs dziobowy , zwany także wstrząsem oderwanym lub wstrząsem normalnym , to zakrzywiona rozchodząca się fala zakłócająca charakteryzująca się nagłą, prawie nieciągłą zmianą ciśnienia , temperatury i gęstości . Występuje, gdy przepływ naddźwiękowy napotyka ciało, wokół którego wymagany kąt odchylenia przepływu jest większy niż maksymalny możliwy do osiągnięcia kąt odchylenia dla dołączonego wstrząsu skośnego (patrz kryterium oderwania). Następnie ukośny wstrząs przekształca się w zakrzywioną, oderwaną falę uderzeniową. Ponieważ wstrząsy dziobowe występują przy dużych kątach odchylenia przepływu, często można je zobaczyć wokół tępych ciał, ze względu na duży kąt odchylenia, jaki ciało narzuca przepływowi wokół niego.
Transformacja termodynamiczna w wyniku uderzenia dziobowego nie jest izentropowa, a szok zmniejsza prędkość przepływu z prędkości naddźwiękowej w górę rzeki do prędkości poddźwiękowej w dole rzeki.
Aplikacje
Amortyzator dziobowy znacznie zwiększa opór w pojeździe poruszającym się z prędkością ponaddźwiękową. Ta właściwość została wykorzystana przy projektowaniu kapsuł powrotnych podczas misji kosmicznych, takich jak program Apollo , które wymagają dużego oporu, aby zwolnić podczas ponownego wejścia w atmosferę .
Relacje szokowe
Podobnie jak w przypadku szoku normalnego i szoku ukośnego ,
- Ciśnienia statyczne przed zaworem są niższe niż ciśnienie statyczne za zaworem .
- Gęstość statyczna po stronie wlotowej jest niższa niż gęstość statyczna po stronie wylotowej.
- Temperatura statyczna powyżej jest niższa niż temperatura statyczna poniżej .
- Całkowite ciśnienie przed zaworem jest większe niż ciśnienie całkowite za zaworem .
- Całkowita gęstość powyżej jest niższa niż całkowita gęstość poniżej.
- Całkowita temperatura powyżej jest równa całkowitej temperaturze poniżej , ponieważ zakłada się, że fala uderzeniowa jest izentalpiczna .
W przypadku zakrzywionego amortyzatora kąt uderzenia zmienia się, a zatem ma zmienną siłę na całym froncie amortyzatora. Prędkość i wirowość przepływu po wstrząsie można zatem obliczyć za pomocą twierdzenia Crocco , które jest niezależne od jakiegokolwiek EOS ( równania stanu ) przy założeniu przepływu nielepkiego .
Zobacz też
- Landau, LD; Lifszyc, EM (2005) [1959]. Mechanika płynów 2. wydanie . Elsevier . ISBN 978-0-7506-2767-2 .
- Courant, R.; Friedrichs KO (1956) [1948]. Przepływ naddźwiękowy i fale uderzeniowe . Nowy Jork: Wydawcy Interscience.