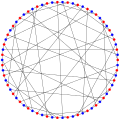
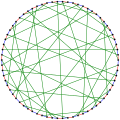
Wykres Harriesa-Wonga

Wykres Harriesa-Wonga Wykres
Harriesa-Wonga
Nazwany po	W. Harries, Pak-Ken Wong
Wierzchołki	70
Krawędzie	105
Promień	6
Średnica	6
Obwód	10
Automorfizmy	24 ( S4 )
Liczba chromatyczna	2
Indeks chromatyczny	3
Grubość książki	3
Numer kolejki	2
Nieruchomości	Hamiltonian bez trójkątów sześciennych
Tabela wykresów i parametrów

W matematycznej dziedzinie teorii grafów graf Harriesa-Wonga jest 3- regularnym grafem nieskierowanym z 70 wierzchołkami i 105 krawędziami.

Wykres Harriesa-Wonga ma liczbę chromatyczną 2, indeks chromatyczny 3, promień 6, średnicę 6, obwód 10 i jest hamiltonowski . Jest to również nieplanarny graf sześcienny połączony 3 wierzchołkami i 3 krawędziami . Ma grubość książki 3 i numer kolejki 2.

Charakterystyczny wielomian wykresu Harriesa-Wonga to

${\ Displaystyle (x-3) (x-1) ^ {4} (x + 1) ^ {4} (x + 3) (x ^ {2} -6) (x ^ {2} -2) ( x^{4}-6x^{2}+2)^{5}(x^{4}-6x^{2}+3)^{4}(x^{4}-6x^{2}+ 6)^{5}.\,}$

Historia

W 1972 roku AT Balaban opublikował graf klatek (3-10), graf sześcienny, który ma jak najmniej wierzchołków dla obwodu 10. Była to pierwsza odkryta klatka (3-10), ale nie była wyjątkowa.

Pełną listę klatek (3-10) i dowód minimalności podali O'Keefe i Wong w 1980 r. Istnieją trzy różne wykresy klatek (3-10) — klatka Balabana z 10 klatkami , wykres Harriesa i wykres Harriesa-Wonga. Ponadto wykres Harriesa-Wonga i wykres Harriesa są grafami kospektralnymi .

Galeria

• 

  Liczba chromatyczna wykresu Harriesa-Wonga wynosi 2.

• 

  Indeks chromatyczny wykresu Harriesa-Wonga wynosi 3.

• 

  Alternatywny rysunek wykresu Harriesa-Wonga.

• 

  8 orbit wykresu Harriesa-Wonga.