Wzajemność (sieci elektryczne)

Wzajemność w sieciach elektrycznych jest właściwością obwodu, który wiąże napięcia i prądy w dwóch punktach. Twierdzenie o wzajemności mówi, że prąd w jednym punkcie obwodu wywołany napięciem w drugim punkcie jest taki sam jak prąd w drugim punkcie wywołany tym samym napięciem w pierwszym. Twierdzenie o wzajemności jest ważne dla prawie wszystkich sieci pasywnych . Twierdzenie o wzajemności jest cechą bardziej ogólnej zasady wzajemności w elektromagnetyzmie .

Opis

Jeśli prąd $displaystyle I _ {\ tekst {A}}}$ do portu $ja$ wytwarza napięcie w $porcie$$\ displaystyle$ ZA { \ displaystyle V _ } } wstrzyknięty do portu B wytwarza $A$ , wtedy mówi się, że sieć jest odwrotna. Równoważnie, wzajemność może być zdefiniowana przez podwójną sytuację; przykładając napięcie, ${\ Displaystyle V _ {\ tekst {A}}}$ w porcie A produkującym prąd ${\ displaystyle I _ {\ tekst {B}}}$ w porcie B i ${\ displaystyle V _ {\ tekst {A}}} w porcie$$A.$ wytwarza prąd w porcie Ogólnie rzecz biorąc, pasywne są wzajemne . Dowolna sieć, która składa się wyłącznie z idealnych pojemności , indukcyjności (w tym indukcyjności wzajemnych ) i rezystancji , czyli elementów, które są liniowy i dwustronny, będzie wzajemny. Istnieją jednak elementy pasywne, które nie są wzajemne. Każdy element zawierający ferromagnetyczny prawdopodobnie nie będzie wzajemny. Przykłady elementów pasywnych celowo zaprojektowanych jako niewzajemne obejmują cyrkulatory i izolatory .

Funkcja przenoszenia sieci odwrotnej ma tę właściwość, że jest symetryczna względem głównej przekątnej , jeśli jest wyrażona za pomocą parametru z , parametru y lub macierzy parametrów s . Niesymetryczna macierz oznacza nieodwrotną sieć. Symetryczna macierz nie implikuje symetrycznej sieci .

W niektórych parametryzacjach sieci reprezentatywna macierz nie jest symetryczna dla sieci odwrotnych. Typowymi przykładami są h-parameters i ABCD-parameters , ale wszystkie mają inny warunek wzajemności, który można obliczyć na podstawie parametrów. Dla parametrów h warunkiem jest ${\ Displaystyle h_ {12} = - h_ {21}},$ a dla parametrów ABCD jest to ${\ displaystyle AD-BC = 1}$ . Te reprezentacje mieszają napięcia i prądy w tym samym wektorze kolumnowym , a zatem nie mają nawet pasujących jednostek w transponowanych elementach.

Przykład

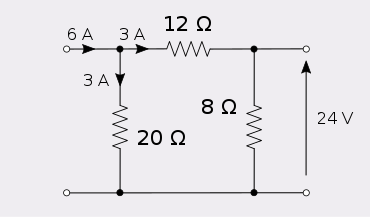
Przykład wzajemności można zademonstrować za pomocą asymetrycznego tłumika rezystancyjnego . Jako przykład wybrano sieć asymetryczną, ponieważ sieć symetryczna jest w oczywisty sposób odwrotna.

Wstrzyknięcie sześciu amperów do portu 1 tej sieci wytwarza 24 wolty na porcie 2.

Wstrzyknięcie sześciu amperów do portu 2 wytwarza 24 wolty na porcie 1.

Sieć jest więc wzajemna. W tym przykładzie port, który nie dostarcza prądu, pozostaje otwarty. Dzieje się tak, ponieważ generator prądu stosujący prąd zerowy jest obwodem otwartym. Z drugiej strony, gdyby ktoś chciał przyłożyć napięcie i zmierzyć wynikowy prąd, to port, do którego nie jest przyłożone napięcie, zostałby zwarty. Dzieje się tak, ponieważ generator napięcia stosujący zero woltów jest zwarciem.

Dowód

Wzajemność sieci elektrycznych jest szczególnym przypadkiem wzajemności Lorentza , ale można ją również udowodnić bardziej bezpośrednio z twierdzeń o sieci. Ten dowód pokazuje wzajemność dla sieci dwuwęzłowej pod względem jej admitancji , a następnie pokazuje wzajemność dla sieci z dowolną liczbą węzłów za pomocą argumentu indukcyjnego . Sieć liniową można przedstawić jako zestaw równań liniowych za pomocą analizy węzłowej . Dla sieci składającej się z n +1 węzły (jeden jest węzłem referencyjnym), gdzie ogólnie rzecz biorąc, między każdą parą węzłów jest połączony wstęp i gdzie w każdym węźle jest wprowadzany prąd (zapewniony przez idealne źródło prądu połączone między węzłem a węzłem referencyjnym), równania te można wyrazić w postaci macierzy admitancji,

${\ Displaystyle {\ rozpocząć {bmatrix} I_ {1} \\ I_ {2} \\\ vdots \\ I_ {n} \ koniec {bmatrix}} = {\ rozpocząć {bmatrix} Y_ {11} i Y_ {12} &\cdots &Y_{1n}\\Y_{21}&Y_{22}&\cdots &Y_{2n}\\\vdots &\vdots &\ddots &\vdots \\Y_{n1}&Y_{n2}&\cdots &Y_{nn}\end{bmatrix}}{\begin{bmatrix}V_{1}\\V_{2}\\\vdots \\V_{n}\end{bmatrix}}}$

Gdzie

$I_ {k}}$ to prąd wtryskiwany do węzła przez generator (który wynosi zero, jeśli żadne źródło prądu nie jest podłączone do węzła ) to

$k$ napięcie w węźle k w odniesieniu do węzła odniesienia (można również powiedzieć, że jest to potencjał elektryczny w węźle k )

${\ Displaystyle Y_ {jk}}$ ( j ≠ k ) jest minusem admitancji bezpośrednio łączącej węzły j a k (jeśli istnieje)

$)$ sumą dopuszczeń połączonych z węzłem ( niezależnie od innego węzła, z którym dopuszczenie jest połączone

Reprezentacja ta odpowiada reprezentacji uzyskanej za pomocą analizy węzłowej . Jeśli dodatkowo wymagamy, aby sieć składała się z pasywnych, dwustronnych elementów, to tak

${\ Displaystyle Y_ {jk} = Y_ {kj}}$

ponieważ admitancja związana między węzłami j i k jest tym samym elementem, co admitancja związana między węzłami k i j . Macierz jest zatem symetryczna. W przypadku, gdy macierz redukuje się do, ${\ displaystyle n = 2}$

${\ Displaystyle {\ rozpocząć {bmatrix} I_ {1} \\ I_ {2} \ koniec {bmatrix}} = { \begin{bmatrix}Y_{11}&Y_{12}\\Y_{21}&Y_{22}\end{bmatrix}}{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix} }}$ .

Z którego widać, że

${\ Displaystyle Y_ {12} = \ lewo. {\ Frac {I_ {1}} {V_ {2}}} \ prawo | _ {V_ {1} = 0}}$ i

${\ Displaystyle Y_ {21} = \ lewo. {\ Frac {I_ {2}} {V_ {1}}} \ prawo | _ {V_ {2} = 0} \ .}$

Ale ponieważ ${\ Displaystyle Y_ {12} = Y_ {21}}$ to,

${\ Displaystyle \ lewo. {\ Frac {I_ {1}} {V_ {2}}} \ prawo | _ {V_ {1} = 0} = \ lewo. {\ Frac {I_ {2}} {V_{1}}}\prawo|_{V_{2}=0}}$

co jest równoznaczne z warunkiem wzajemności. Innymi słowy, stosunek prądu na jednym porcie do napięcia na drugim jest taki sam, jeśli porty napędzane i mierzone są zamienione. Zatem wzajemność jest udowodniona w przypadku ${\ displaystyle n = 2}$ .

W przypadku macierzy o dowolnym rozmiarze, kolejność macierzy można zmniejszyć poprzez eliminację węzłów . Po wyeliminowaniu s -tego węzła nowa macierz admitancji będzie miała postać,

${\ Displaystyle {\ rozpocząć {bmatrix} (Y_ {11} Y_ {ss} -Y_ {s1} Y_ {1s}) i (Y_ {12} Y_ {ss} - Y_ {s2} Y_ {1s}) i ( Y_{13}Y_{ss}-Y_{s3}Y_{1s})&\cdots \\(Y_{21}Y_{ss}-Y_{s1}Y_{2s})&(Y_{22}Y_{ ss}-Y_{s2}Y_{2s})&(Y_{23}Y_{ss}-Y_{s3}Y_{2s})&\cdots \\(Y_{31}Y_{ss}-Y_{s1 }Y_{3s})&(Y_{32}Y_{ss}-Y_{s2}Y_{3s})&(Y_{33}Y_{ss}-Y_{s3}Y_{3s})&\cdots \ \\cdots &\cdots &\cdots &\cdots \end{bmatrix}}}$

Można zauważyć, że ta nowa macierz jest również symetryczna. Węzły można nadal eliminować w ten sposób, aż pozostanie tylko symetryczna macierz 2 × 2 obejmująca dwa interesujące nas węzły. Ponieważ ta macierz jest symetryczna, udowodniono, że wzajemność ma zastosowanie do macierzy o dowolnym rozmiarze, gdy jeden węzeł jest napędzany przez napięcie i prąd mierzone w innym. Podobny proces wykorzystujący macierz impedancji z analizy siatki pokazuje wzajemność, w której jeden węzeł jest zasilany prądem, a napięcie jest mierzone w innym.

Bibliografia

•   Bakshi, UA; Bakshi, AV, Sieci elektryczne , publikacje techniczne, 2008 ISBN 8184314647 .
•   Guillemin, Ernst A., Wstępna teoria obwodów , Nowy Jork: John Wiley & Sons, 1953 OCLC 535111
•   Kumar, KS Suresh, Obwody elektryczne i sieci , Pearson Education India, 2008 ISBN 8131713903 .
•   Harris, Vincent G., „Ferryty mikrofalowe i zastosowania”, rozdz. 14 w, Mailadil T. Sebastian, Rick Ubic, Heli Jantunen, Materiały i zastosowania mikrofalowe , John Wiley & Sons, 2017 ISBN 1119208521 .
•   Zhang, Kequian; Li, Dejie, Teoria elektromagnetyczna dla mikrofal i optoelektroniki , Springer Science & Business Media, 2013 ISBN 3662035537 .