Zasada 90
W matematycznym badaniu automatów komórkowych Reguła 90 jest podstawowym automatem komórkowym opartym na wyłączności lub funkcji. Składa się z jednowymiarowej tablicy komórek, z których każda może zawierać wartość 0 lub 1. W każdym kroku czasowym wszystkie wartości są jednocześnie zastępowane przez wartość wyłączną lub dwie sąsiednie. Martin, Odlyzko i Wolfram (1984) nazywają to „najprostszym nietrywialnym automatem komórkowym” i jest obszernie opisany w książce Stephena Wolframa z 2002 roku Nowy rodzaj nauki .
Po uruchomieniu z pojedynczej żywej komórki Reguła 90 ma diagram czasoprzestrzenny w postaci trójkąta Sierpińskiego . Zachowanie dowolnej innej konfiguracji można wyjaśnić jako superpozycję kopii tego wzorca, połączonych za pomocą wyłączności lub . Każda konfiguracja z tylko skończenie wieloma niezerowymi komórkami staje się replikatorem , który ostatecznie wypełnia macierz swoimi kopiami. Gdy Reguła 90 rozpoczyna się od losowej początkowej konfiguracji, jej konfiguracja pozostaje losowa w każdym kroku czasowym. Jego diagram czasoprzestrzenny tworzy wiele trójkątnych "okien" o różnej wielkości, wzorców, które tworzą się, gdy kolejny rząd komórek staje się jednocześnie zerem, a następnie komórki o wartości 1 stopniowo przesuwają się do tego rzędu z obu końców.
Niektóre z najwcześniejszych badań Reguły 90 zostały wykonane w związku z nierozwiązanym problemem w teorii liczb , hipotezą Gilbreatha , dotyczącą różnic kolejnych liczb pierwszych . Reguła ta jest również połączona z teorią liczb w inny sposób, poprzez sekwencję Goulda . Sekwencja ta zlicza niezerową liczbę komórek w każdym kroku czasowym po rozpoczęciu Reguły 90 z pojedynczą żywą komórką. Jego wartości są potęgami dwójki , z wykładnikami równymi liczbie cyfr niezerowych w reprezentacji binarnej numeru kroku. Inne zastosowania Reguły 90 obejmowały projektowanie gobelinów .
Każda konfiguracja Reguły 90 ma dokładnie czterech poprzedników, inne konfiguracje, które tworzą daną konfigurację po jednym kroku. Dlatego w przeciwieństwie do wielu innych automatów komórkowych, takich jak gra w życie Conwaya , Reguła 90 nie ma rajskiego ogrodu , konfiguracji bez poprzedników. Podaje przykład automatu komórkowego, który jest suriekcyjny (każda konfiguracja ma poprzednika), ale nie iniekcyjny (posiada zestawy więcej niż jednej konfiguracji z tym samym następcą). Wynika to z twierdzenia Ogrodu Eden że reguła 90 jest lokalnie iniekcyjna (wszystkie konfiguracje z tym samym następcą różnią się w nieskończonej liczbie komórek).
Opis
Zasady
Reguła 90 jest podstawowym automatem komórkowym . Oznacza to, że składa się z jednowymiarowej tablicy komórek, z których każda zawiera pojedynczą wartość binarną, 0 lub 1. Przypisanie wartości do wszystkich komórek nazywa się konfiguracją . Automat otrzymuje początkową konfigurację, a następnie przechodzi przez kolejne konfiguracje w sekwencji dyskretnych kroków czasowych. Na każdym etapie wszystkie komórki są aktualizowane jednocześnie. Z góry określona reguła określa nową wartość każdej komórki jako funkcję jej poprzedniej wartości oraz wartości w dwóch sąsiednich komórkach. Wszystkie komórki podlegają tej samej regule, która może być podana jako formuła lub jako tabela reguł określająca nową wartość dla każdej możliwej kombinacji sąsiednich wartości.
W przypadku Reguły 90 nowa wartość każdej komórki jest wartością wyłączną lub wartością dwóch sąsiadujących ze sobą wartości. Równoważnie, następny stan tego konkretnego automatu jest regulowany przez następującą tabelę reguł:
| aktualny wzór | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| nowy stan dla komórki środkowej | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Nazewnictwo
Nazwa reguły 90 pochodzi od binarno-dziesiętnej notacji Stephena Wolframa dla jednowymiarowych reguł automatów komórkowych. Aby obliczyć notację dla reguły, połącz nowe stany w tabeli reguł w pojedynczą liczbę binarną i zamień ją na dziesiętną : 01011010 2 = 90 10 . Reguła 90 została również nazwana automatem Sierpińskiego , ze względu na charakterystyczny kształt trójkąta Sierpińskiego , który generuje, oraz automat komórkowy Martina – Odlyzko – Wolframa po wczesnych badaniach Oliviera Martina, Andrew M. Odlyzko i Stephena Wolframa ( 1984 ) nad tym automatem.
Nieruchomości
Addytywność, superpozycja i rozkład
Konfiguracja w regule 90 może być podzielona na dwa podzbiory komórek, które nie wchodzą ze sobą w interakcje. Jeden z tych dwóch podzbiorów składa się z komórek w parzystych pozycjach w parzystych odstępach czasu i komórek w nieparzystych pozycjach w nieparzystych odstępach czasu. Drugi podzbiór składa się z komórek w parzystych pozycjach w nieparzystych krokach czasowych i komórek w nieparzystych pozycjach w parzystych krokach czasowych. Każdy z tych dwóch podzbiorów można postrzegać jako automat komórkowy z tylko połową komórek. Reguła dla automatu w każdym z tych podzbiorów jest równoważna (z wyjątkiem przesunięcia o pół komórki na krok czasowy) z innym elementarnym automatem komórkowym , Reguła 102 , w którym nowy stan każdej komórki jest wyłączny lub jej starego stanu i jej prawego sąsiada. Oznacza to, że zachowanie Reguły 90 jest zasadniczo takie samo, jak zachowanie dwóch przeplatanych kopii Reguły 102.
Reguła 90 i Reguła 102 nazywane są addytywnymi automatami komórkowymi . Oznacza to, że jeśli dwa stany początkowe zostaną połączone przez obliczenie wyłączności lub każdego z ich stanów, to ich kolejne konfiguracje zostaną połączone w ten sam sposób. Mówiąc bardziej ogólnie, można podzielić dowolną konfigurację reguły 90 na dwa podzbiory z rozłącznymi niezerowymi komórkami, oddzielnie rozwinąć dwa podzbiory i obliczyć każdą kolejną konfigurację oryginalnego automatu jako wyłączną lub konfiguracji w tym samym kroku czasowym dwóch podzbiorów .
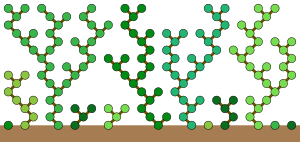
Karłowate drzewa i trójkątne polany
Automat Reguły 90 (w jego równoważnej formie w jednym z dwóch niezależnych podzbiorów naprzemiennych komórek) był badany na początku lat siedemdziesiątych, próbując uzyskać dodatkowy wgląd w hipotezę Gilbreatha dotyczącą różnic kolejnych liczb pierwszych . W trójkącie liczb generowanych z liczb pierwszych przez wielokrotne stosowanie przedniego operatora różnicy , wydaje się, że większość wartości to 0 lub 2. W szczególności przypuszczenie Gilbreatha zakłada, że wszystkie skrajne lewe wartości w każdym rzędzie tego trójkąta to 0 lub 2. Kiedy ciągła podsekwencja wartości w jednym rzędzie trójkąta to wszystkie 0 lub 2, wówczas przepis 90 może być użyty do określenia odpowiedniej podsekwencji w następnym rzędzie. Millera (1970) wyjaśnił regułę metaforą wzrostu drzew w lesie, zatytułowaną swój artykuł na temat „Lasy okresowe karłowatych drzew”. W tej metaforze drzewo zaczyna rosnąć w każdej pozycji początkowej konfiguracji, której wartość wynosi 1, a następnie ten las drzew rośnie jednocześnie, na nową wysokość nad ziemią w każdym kroku czasowym. Każda niezerowa komórka w każdym kroku czasowym reprezentuje pozycję zajmowaną przez rosnącą gałąź drzewa. W każdym kolejnym kroku czasowym gałąź może wyrosnąć na jedną z dwóch komórek znajdujących się nad nią po lewej i prawej stronie tylko wtedy, gdy nie ma innej gałęzi konkurującej o tę samą komórkę. Las drzew rosnących zgodnie z tymi zasadami zachowuje się dokładnie tak samo, jak Reguła 90.
Z dowolnej początkowej konfiguracji Reguły 90 można utworzyć las matematyczny , skierowany graf acykliczny , w którym każdy wierzchołek ma co najwyżej jedną krawędź wychodzącą, którego drzewa są takie same jak drzewa w metaforze Millera. Las ma wierzchołek dla każdej pary ( x , i ) taki , że komórka x jest różna od zera w czasie i . Wierzchołki w czasie 0 nie mają wychodzących krawędzi; każdy tworzy korzeń drzewa w lesie. Dla każdego wierzchołka ( x , i ) przy i niezerowym, jego wychodząca krawędź przechodzi do ( x ± 1, i - 1) , unikalnego niezerowego sąsiada x w kroku czasowym i - 1 . Miller zauważył, że lasy te tworzą trójkątne „polany”, obszary diagramu czasoprzestrzennego bez komórek niezerowych, ograniczone płaską dolną krawędzią i ukośnymi bokami. Taka prześwit powstaje, gdy kolejna sekwencja komórek staje się jednocześnie zerem w jednym kroku czasowym, a następnie (w metaforze drzewa) gałęzie rosną do wewnątrz, ostatecznie ponownie pokrywając komórki sekwencji.
W przypadku losowych warunków początkowych granice między utworzonymi w ten sposób drzewami przesuwają się w pozornie przypadkowy sposób, a drzewa często całkowicie obumierają. Ale dzięki teorii rejestrów przesuwnych on i inni byli w stanie znaleźć warunki początkowe, w których wszystkie drzewa pozostają żywe na zawsze, wzorzec wzrostu powtarza się okresowo i można zagwarantować, że wszystkie polany pozostaną ograniczone pod względem wielkości. Miller wykorzystał te powtarzające się wzory do tworzenia projektów gobelinów . Niektóre gobeliny Millera przedstawiają fizyczne drzewa; inni wizualizują automat Reguły 90 za pomocą abstrakcyjnych wzorów trójkątów.
Trójkąt Sierpińskiego

Diagram czasoprzestrzenny reguły 90 jest wykresem, w którym i- ty wiersz rejestruje konfigurację automatu w kroku i . Kiedy stan początkowy ma pojedynczą niezerową komórkę, ten diagram ma wygląd trójkąta Sierpińskiego , fraktala utworzonego przez połączenie trójkątów w większe trójkąty. Reguły 18, 22, 26, 82, 146, 154, 210 i 218 również generują trójkąty Sierpińskiego z pojedynczej komórki, jednak nie wszystkie z nich są tworzone całkowicie identycznie. Jednym ze sposobów wyjaśnienia tej struktury jest fakt, że w regule 90 każda komórka jest wyłącznym lub swoich dwóch sąsiadów. Ponieważ jest to równoważne z modulo -2, generuje to wersję modulo-2 trójkąta Pascala . Diagram ma 1 wszędzie tam, gdzie trójkąt Pascala ma liczbę nieparzystą , a 0 wszędzie tam, gdzie trójkąt Pascala ma liczbę parzystą . Jest to dyskretna wersja trójkąta Sierpińskiego.
Liczba żywych komórek w każdym rzędzie tego wzoru jest potęgą dwójki . W i -tym wierszu jest równa 2 k , gdzie k jest liczbą niezerowych cyfr w binarnej reprezentacji liczby i . Sekwencja tych liczb żywych komórek,
- 1, 2, 2, 4, 2, 4, 4, 8, 2, 4, 4, 8, 4, 8, 8, 16, 2, 4, 4, 8, 4, 8, 8, 16, 4, 8, 8, 16, 8, 16, 16, 32, ... (sekwencja A001316 w OEIS )
jest znany jako ciąg Goulda . Pojedyncza żywa komórka początkowej konfiguracji to wzór piłokształtny . Oznacza to, że w niektórych krokach czasowych liczba żywych komórek rośnie arbitralnie, podczas gdy w innych wracają do zaledwie dwóch żywych komórek, nieskończenie często. Tempo wzrostu tego wzorca ma charakterystyczny rosnący fali piłokształtnej , który można wykorzystać do rozpoznania procesów fizycznych, które zachowują się podobnie do Reguły 90.
Trójkąt Sierpińskiego pojawia się również w bardziej subtelny sposób w ewolucji dowolnej konfiguracji Reguły 90. Na dowolnym etapie i ewolucji Reguły stan dowolnej komórki można obliczyć jako wyłączny lub podzbiór komórek w wstępna konfiguracja. Podzbiór ten ma taki sam kształt jak i- ty rząd trójkąta Sierpińskiego.
Replikacja
W trójkącie Sierpińskiego dla dowolnej liczby całkowitej i wiersze ponumerowane wielokrotnością 2 i mają niezerowe komórki oddalone od siebie o co najmniej 2 i jednostki. Dlatego, ze względu na addytywną właściwość reguły 90, jeśli początkowa konfiguracja składa się ze skończonego wzoru P niezerowych komórek o szerokości mniejszej niż 2 i , to w krokach, które są wielokrotnościami 2 i , konfiguracja będzie się składać z kopii P rozmieszczonych co najmniej 2 I jednostki od początku do początku. Odstęp ten jest wystarczająco szeroki, aby kopie nie kolidowały ze sobą. Liczba kopii jest taka sama, jak liczba niezerowych komórek w odpowiednim rzędzie trójkąta Sierpińskiego. Zatem w tej regule każdy wzorzec jest replikatorem : generuje wiele swoich kopii, które rozprzestrzeniają się w konfiguracji, ostatecznie wypełniając całą tablicę. Inne reguły, w tym uniwersalny konstruktor Von Neumanna , automat komórkowy Codda i pętle Langtona mają również replikatory, które działają poprzez przenoszenie i kopiowanie sekwencji instrukcji do samodzielnego budowania. Natomiast powtórzenie w art. 90 jest trywialne i automatyczne.
Poprzednicy i Ogrody Edenu
W regule 90 na nieskończonej jednowymiarowej siatce każda konfiguracja ma dokładnie cztery poprzednie konfiguracje. Dzieje się tak, ponieważ w poprzedniku dowolne dwie kolejne komórki mogą mieć dowolną kombinację stanów, ale po wybraniu stanów tych dwóch komórek istnieje tylko jeden spójny wybór dla stanów pozostałych komórek. Dlatego w regule 90 nie ma Ogrodu Eden , konfiguracji bez poprzedników. Konfiguracja Reguły 90 składająca się z pojedynczej niezerowej komórki (z wszystkimi innymi komórkami zerowymi) nie ma poprzedników, które mają skończenie wiele niezerowych. Jednak ta konfiguracja nie jest rajskim ogrodem, ponieważ ma poprzedników z nieskończenie wieloma liczbami niezerowymi.
Fakt, że każda konfiguracja ma swój poprzednik, można podsumować stwierdzeniem, że Reguła 90 jest suriekcją . Funkcja, która odwzorowuje każdą konfigurację na jej następcę, jest matematycznie funkcją suriekcji. Reguła 90 również nie jest iniekcyjna . W regule iniekcyjnej każde dwie różne konfiguracje mają różnych następców, ale reguła 90 ma pary konfiguracji z tym samym następnikiem. Reguła 90 podaje przykład automatu komórkowego, który jest surjektywny, ale nie iniekcyjny. Twierdzenie o ogrodzie Eden Moore'a i Myhilla implikuje, że każdy iniekcyjny automat komórkowy musi być surjekcją, ale ten przykład pokazuje, że sytuacja odwrotna nie jest prawdziwa.
Ponieważ każda konfiguracja ma tylko ograniczoną liczbę poprzedników, ewolucja Reguły 90 zachowuje entropię dowolnej konfiguracji. W szczególności, jeśli wybrano nieskończoną konfigurację początkową, wybierając stan każdej komórki niezależnie losowo, przy czym każdy z dwóch stanów jest równie prawdopodobny do wyboru, wówczas każdą kolejną konfigurację można opisać dokładnie tym samym rozkładem prawdopodobieństwa.
Emulacja przez inne systemy
Wiele innych automatów komórkowych i innych systemów obliczeniowych jest w stanie naśladować zachowanie Reguły 90. Na przykład konfiguracja w regule 90 może zostać przetłumaczona na konfigurację innego podstawowego automatu komórkowego Reguła 22. Translacja zastępuje każdą komórkę Reguły 90 trzema kolejne komórki Reguły 22. Wszystkie te komórki są zerowe, jeśli komórka Reguły 90 sama jest zerem. Niezerowa komórka Reguły 90 jest tłumaczona na jedynkę, po której następują dwa zera. Dzięki tej transformacji każde sześć kroków automatu według reguły 22 symuluje pojedynczy krok automatu według reguły 90. Podobne bezpośrednie symulacje Reguły 90 są również możliwe dla elementarnych automatów komórkowych Reguła 45 i Reguła 126, dla niektórych systemy przepisywania ciągów i systemy znaczników oraz w niektórych dwuwymiarowych automatach komórkowych, w tym Wireworld . Reguła 90 może również symulować się w ten sam sposób. Jeżeli każda komórka konfiguracji z Reguły 90 zostanie zastąpiona parą kolejnych komórek, z których pierwsza zawiera pierwotną wartość komórki, a druga zawiera zero, wówczas ta podwojona konfiguracja zachowuje się tak samo jak konfiguracja pierwotna przy połowie prędkości.
Wiadomo, że różne inne automaty komórkowe obsługują replikatory, wzorce, które same siebie kopiują, a większość zachowuje się tak samo, jak w modelu wzrostu drzewa dla Reguły 90. Nowa kopia jest umieszczana po obu stronach wzorca replikatora, o ile miejsce tam jest puste. Jeśli jednak oba replikatory spróbują skopiować się w to samo miejsce, miejsce pozostanie puste. W obu przypadkach same replikatory znikają, pozostawiając swoje kopie, aby kontynuowały replikację. Standardowym przykładem takiego zachowania jest wzór „muszka makaron” w dwuwymiarowym HighLife reguła. Zasada ta zachowuje się na wiele sposobów jak gra w życie Conwaya, ale tak mały replikator nie istnieje w życiu. wzorze wzrostu, do symulacji Reguły 90 można użyć jednowymiarowych macierzy replikatorów. Reguła 90 (na skończonych rzędach komórek) może być również symulowana przez oscylatory blokowe dwuwymiarowego automat komórkowy B36/S125, zwany także "2x2", oraz zachowanie reguły 90 może być użyte do scharakteryzowania możliwych okresów tych oscylatorów.
Zobacz też
- Inne elementarne automaty komórkowe: Reguła 30 , Reguła 110 i Reguła 184