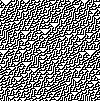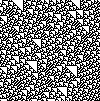Podstawowy automat komórkowy

Animacja przedstawiająca sposób określania ewolucji w regule 30, jednej z 256 możliwych reguł elementarnych automatów komórkowych.

W matematyce i teorii obliczalności elementarny automat komórkowy jest jednowymiarowym automatem komórkowym , w którym istnieją dwa możliwe stany (oznaczone 0 i 1), a reguła określania stanu komórki w następnym pokoleniu zależy tylko od aktualnego stanu komórka i jej dwóch bezpośrednich sąsiadów. Istnieje elementarny automat komórkowy ( reguła 110 , zdefiniowana poniżej), który jest zdolny do obliczeń uniwersalnych i jako taki jest jednym z najprostszych możliwych modeli obliczeń.

System numeracji

Istnieje 8 = 2 ³ możliwych konfiguracji komórki i jej dwóch bezpośrednich sąsiadów. Reguła definiująca automat komórkowy musi określać wynikowy stan dla każdej z tych możliwości, więc istnieje 256 = 2 ^{2 ³} możliwych elementarnych automatów komórkowych. Stephen Wolfram zaproponował schemat, znany jako kod Wolframa , aby przypisać każdej regule numer od 0 do 255, który stał się standardem. Każda możliwa bieżąca konfiguracja jest zapisywana w kolejności 111, 110, ..., 001, 000, a stan wynikowy dla każdej z tych konfiguracji jest zapisywany w tej samej kolejności i interpretowany jako binarna reprezentacja liczby całkowitej. Ta liczba jest traktowana jako numer reguły automatu. Na przykład 110 _d = 01101110 ₂ . Tak więc przepis 110 jest zdefiniowany przez przepis przejściowy:

111	110	101	100	011	010	001	000	aktualny wzór	P=(L,C,R)
0	1	1	0	1	1	1	0	nowy stan dla komórki środkowej	N _{110 _d} = (C+R+CR+LC*R)%2

Refleksje i uzupełnienia

Chociaż istnieje 256 możliwych reguł, wiele z nich jest trywialnie równoważnych sobie nawzajem, aż do prostej transformacji podstawowej geometrii. Pierwszym takim przekształceniem jest odbicie przez oś pionową, a wynik zastosowania tego przekształcenia do danej reguły nazywany jest regułą lustrzaną . Reguły te będą wykazywać to samo zachowanie aż do odbicia przez oś pionową, a więc są równoważne w sensie obliczeniowym.

Na przykład, jeżeli definicja przepisu 110 jest odzwierciedlona przez linię pionową, otrzymuje się następujący przepis (przepis 124):

111	110	101	100	011	010	001	000	aktualny wzór	P=(L,C,R)
0	1	1	1	1	1	0	0	nowy stan dla komórki środkowej	N _{112 _d +12 _d =124 _d} =(L+C+LC+LC*R)%2

Reguły, które są takie same, jak ich lustrzana reguła, nazywane są amphichiralnymi . Spośród 256 elementarnych automatów komórkowych 64 są amfichiralne.

Druga taka transformacja polega na zamianie ról 0 i 1 w definicji. Wynik zastosowania tego przekształcenia do danej reguły nazywany jest regułą komplementarną . Na przykład, jeśli to przekształcenie zostanie zastosowane do reguły 110, otrzymamy następującą regułę

aktualny wzór	000	001	010	011	100	101	110	111
nowy stan dla komórki środkowej	1	0	0	1	0	0	0	1

i po zmianie kolejności odkrywamy, że jest to zasada 137:

aktualny wzór	111	110	101	100	011	010	001	000
nowy stan dla komórki środkowej	1	0	0	0	1	0	0	1

Istnieje 16 zasad, które są takie same, jak ich zasady uzupełniające.

Wreszcie, poprzednie dwie transformacje można kolejno zastosować do reguły, aby uzyskać lustrzaną regułę komplementarną. Na przykład lustrzanym przepisem uzupełniającym przepisu 110 jest przepis 193. Jest 16 przepisów, które są takie same, jak ich lustrzane przepisy uzupełniające.

Spośród 256 elementarnych automatów komórkowych 88 jest nierównoważnych przy tych przekształceniach.

Pojedyncze 1 historie

Jedną z metod wykorzystywanych do badania tych automatów jest śledzenie ich historii ze stanem początkowym zawierającym wszystkie zera z wyjątkiem pojedynczej komórki z 1. Kiedy liczba reguł jest parzysta (tak, że wejście 000 nie daje 1), to sprawia, że sens interpretowania stanu w każdym momencie, t , jako liczby całkowitej wyrażonej binarnie, tworząc ciąg a ( t ) liczb całkowitych. W wielu przypadkach sekwencje te mają proste, zamknięte formy wyrażeń lub mają funkcję generującą o prostej formie. Godne uwagi są następujące zasady:

Zasada 28

Wygenerowana sekwencja to 1, 3, 5, 11, 21, 43, 85, 171, ... (sekwencja A001045 w OEIS ). To jest sekwencja liczb Jacobsthala i ma funkcję generującą

{\ Displaystyle {\ Frac {1 + 2x} {(1 + x) (1-2x)}}}

.

Ma wyrażenie w formie zamkniętej

{\ Displaystyle a (t) = {\ Frac {4 \ cdot 2 ^ {t} - (-1) ^ {t}} {3}} }

Reguła 156 generuje tę samą sekwencję.

Zasada 50

Wygenerowana sekwencja to 1, 5, 21, 85, 341, 1365, 5461, 21845, ... (sekwencja A002450 w OEIS ). Ma to funkcję generującą

{\ Displaystyle {\ Frac {1} {(1-x) (1-4x)}}}

.

Ma wyrażenie w formie zamkniętej

{\ Displaystyle a (t) = {\ Frac {4 \ cdot 4 ^ {t} -1} {3}}}

.

Należy zauważyć, że reguły 58, 114, 122, 178, 186, 242 i 250 generują tę samą sekwencję.

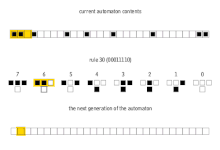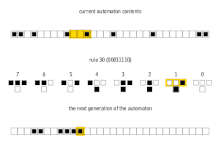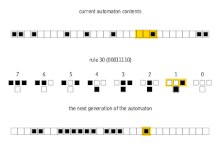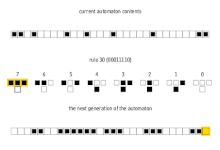
Reguła 54

Wygenerowana sekwencja to 1, 7, 17, 119, 273, 1911, 4369, 30583, ... (sekwencja A118108 w OEIS ). Ma to funkcję generującą

{\ Displaystyle {\ Frac {1 + 7x} {(1-x ^ {2}) (1-16x ^ {2})}}}

.

Ma wyrażenie w formie zamkniętej

{\ Displaystyle a (t) = {\ Frac {22 \ cdot 4 ^ {t} -6 (- 4)^{t}-4+3(-1)^{t}}{15}}}

.

Reguła 60

Wygenerowana sekwencja to 1, 3, 5, 15, 17, 51, 85, 255, ... (sekwencja A001317 w OEIS ). Można to uzyskać, biorąc kolejne wiersze trójkąta Pascala modulo 2 i interpretując je jako liczby całkowite w systemie binarnym, które można graficznie przedstawić za pomocą trójkąta Sierpińskiego .

Zasada 90

Wygenerowana sekwencja to 1, 5, 17, 85, 257, 1285, 4369, 21845, ... (sekwencja A038183 w OEIS ). Można to uzyskać, biorąc kolejne wiersze trójkąta Pascala modulo 2 i interpretując je jako liczby całkowite o podstawie 4. Zauważ, że reguły 18, 26, 82, 146, 154, 210 i 218 generują tę samą sekwencję.

Zasada 94

Wygenerowana sekwencja to 1, 7, 27, 119, 427, 1879, 6827, 30039, ... (sekwencja A118101 w OEIS ). Można to wyrazić jako

{\ Displaystyle a (t) ={\begin{przypadki}1,&{\mbox{if}}t=0\\[5px]7,&{\mbox{if}}t=1\\[7px]{\dfrac {1+5 \cdot 4^{n}}{3}},&{\mbox{if }}t{\mbox{ jest jeszcze inaczej}}\\[7px]{\dfrac {10+11\cdot 4^{n} }{6}},&{\mbox{if }}t{\mbox{ jest nieparzyste w innym przypadku}}\end{cases}}}

.

Ma to funkcję generującą

{\ Displaystyle {\ Frac {(1 + 2x) (1 + 5x-16x ^ {4 })}{(1-x^{2})(1-16x^{2})}}}

.

Zasada 102

Wygenerowana sekwencja to 1, 6, 20, 120, 272, 1632, 5440, 32640, ... (sekwencja A117998 w OEIS ). Jest to po prostu sekwencja generowana przez regułę 60 (która jest jej lustrzanym odbiciem) pomnożona przez kolejne potęgi 2.

Reguła 110

Wygenerowana sekwencja to 1, 6, 28, 104, 496, 1568, 7360, 27520, 130304, 396800, ... (sekwencja A117999 w OEIS ). Reguła 110 ma być może zaskakującą właściwość, że jest kompletna według Turinga , a zatem zdolna do uniwersalnych obliczeń .

Reguła 150

Wygenerowana sekwencja to 1, 7, 21, 107, 273, 1911, 5189, 28123, ... (sekwencja A038184 w OEIS ). Można to uzyskać, biorąc współczynniki kolejnych potęg (1+ x + x ² ) modulo 2 i interpretując je jako liczby całkowite w systemie binarnym.

Reguła 158

Wygenerowana sekwencja to 1, 7, 29, 115, 477, 1843, 7645, 29491, ... (sekwencja A118171 w OEIS ). Ma to funkcję generującą

{\ Displaystyle {\ Frac {1 + 7x + 12x ^ {2} -4x ^ {3}} {( 1-x^{2})(1-16x^{2})}}}

.

Reguła 188

Wygenerowana sekwencja to 1, 3, 5, 15, 29, 55, 93, 247, ... (sekwencja A118173 w OEIS ). Ma to funkcję generującą

{\ Displaystyle {\ Frac {1 + 3x + 4x ^ {2} + 12x^{3}+8x^{4}-8x^{5}}{(1-x^{2})(1-16x^{4})}}}

.

Reguła 190

Wygenerowana sekwencja to 1, 7, 29, 119, 477, 1911, 7645, 30583, ... (sekwencja A037576 w OEIS ). Ma to funkcję generującą

{\ Displaystyle {\ Frac {1 + 3x} {(1-x ^ {2}) (1-4x)}}}

.

Reguła 220

Wygenerowana sekwencja to 1, 3, 7, 15, 31, 63, 127, 255, ... (sekwencja A000225 w OEIS ). To jest ciąg liczb Mersenne'a i ma funkcję generującą

{\ Displaystyle {\ Frac {1} {(1-x) (1-2x)}}}

.

Ma wyrażenie w formie zamkniętej

{\ Displaystyle a (t) = 2 \ cdot 2 ^ {t} -1}

.

Uwaga: przepis 252 generuje tę samą sekwencję.

Reguła 222

Wygenerowana sekwencja to 1, 7, 31, 127, 511, 2047, 8191, 32767, ... (sekwencja A083420 w OEIS ). Jest to co drugi wpis w ciągu liczb Mersenne'a i ma funkcję generującą

{\ Displaystyle {\ Frac {1 + 2x} {(1-x) (1-4x)}}}

.

Ma wyrażenie w formie zamkniętej

{\ Displaystyle a (t) = 2 \ cdot 4 ^ {t} -1}

.

Zauważ, że przepis 254 generuje tę samą sekwencję.

Obrazy dla reguł 0-99

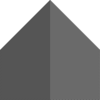
Te obrazy przedstawiają diagramy czasoprzestrzenne, na których każdy rząd pikseli przedstawia komórki automatu w jednym punkcie w czasie, z czasem rosnącym w dół. Zaczynają od początkowego stanu automatu, w którym pojedyncza komórka, piksel w środku górnego rzędu pikseli, jest w stanie 1, a wszystkie inne komórki mają stan 0.

Zasada 0
Zasada nr 1
Zasada 2
Zasada 3
Zasada 4
Zasada 5
Zasada 6
Zasada 7
Zasada 8
Zasada 9
Zasada 10
Zasada 11
Zasada 12
Zasada 13
Zasada 14
Zasada 15
Zasada 16
Zasada 17
Zasada 18
Zasada 19
Zasada 20
Zasada 21
Zasada 22
Zasada 23
Zasada 24
Zasada 25
Zasada 26
Zasada 27
Zasada 28
Zasada 29
Zasada 30
Zasada 31
Zasada 32
Zasada 33
Zasada 34
Zasada 35
Zasada 36
Zasada 37
Zasada 38
Zasada 39
Reguła 40
Zasada 41
Zasada 42
Zasada 43
Reguła 44
Zasada 45
Zasada 46
Zasada 47
Zasada 48
Zasada 49
Zasada 50
Zasada 51
Zasada 52
Zasada 53
Reguła 54
Zasada 55
Zasada 56
Zasada 57
Zasada 58
Zasada 59
Reguła 60
Zasada 61
Zasada 62
Zasada 63
Reguła 64
Reguła 65
Zasada 66
Zasada 67
Zasada 68
Zasada 69
Reguła 70
Reguła 71
Reguła 72
Reguła 73
Reguła 74
Reguła 75
Reguła 76
Reguła 77
Reguła 78
Zasada 79
Reguła 80
Reguła 81
Reguła 82
Reguła 83
Reguła 84
Zasada 85
Zasada 86
Zasada 87
Zasada 88
Zasada 89
Zasada 90
Zasada 91
Zasada 92
Zasada 93
Zasada 94
Zasada 95
Zasada 96
Zasada 97
Zasada 98
Zasada 99

Losowy stan początkowy

Drugim sposobem zbadania zachowania tych automatów jest zbadanie ich historii, zaczynając od losowego stanu. To zachowanie można lepiej zrozumieć w kategoriach klas Wolframa. Wolfram podaje następujące przykłady jako typowe zasady każdej klasy.

Klasa 1: automaty komórkowe, które szybko zbiegają się do stanu jednolitego. Przykładami są zasady 0, 32, 160 i 232.
Klasa 2: Automaty komórkowe, które szybko zbiegają się do powtarzalnego lub stabilnego stanu. Przykładami są zasady 4, 108, 218 i 250.
Klasa 3: automaty komórkowe, które wydają się pozostawać w przypadkowym stanie. Przykładami są zasady 22, 30, 126, 150, 182.
Klasa 4: Automaty komórkowe, które tworzą obszary powtarzalnych lub stabilnych stanów, ale także tworzą struktury, które oddziałują na siebie w skomplikowany sposób. Przykładem jest przepis 110 . Reguła 110 okazała się zdolna do uniwersalnych obliczeń .

Każdy obliczony wynik jest umieszczany pod źródłem tego wyniku, tworząc dwuwymiarową reprezentację ewolucji systemu.

W poniższej galerii ta ewolucja od losowych warunków początkowych jest pokazana dla każdej z 88 nierównoważnych reguł. Poniżej każdego obrazu znajduje się numer reguły użytej do wytworzenia obrazu, aw nawiasach podano numery reguł równoważnych reguł utworzonych przez odbicie lub uzupełnienie, jeśli takie istnieją. Jak wspomniano powyżej, zasada odbicia dawałaby odbity obraz, podczas gdy reguła uzupełniająca dawałaby obraz z zamianą czerni i bieli.

Zasada 0 (255)
Zasada 1 (127)
Reguła 2 (16, 191, 247)
Reguła 3 (17, 63, 119)
Zasada 4 (223)
Zasada 5 (95)
Zasada 6 (20, 159, 215)
Reguła 7 (21, 31, 87)
Zasada 8 (64, 239, 253)
Zasada 9 (65, 111, 125)
Zasada 10 (80, 175, 245)
Zasada 11 (47, 81, 117)
Zasada 12 (68, 207, 221)
Reguła 13 (69, 79, 93)
Reguła 14 (84, 143, 213)
Zasada 15 (85)
Zasada 18 (183)
Zasada 19 (55)
Zasada 22 (151)
Zasada 23
Reguła 24 (66, 189, 231)
Reguła 25 (61, 67, 103)
Reguła 26 (82, 167, 181)
Reguła 27 (39, 53, 83)
Reguła 28 (70, 157, 199)
Zasada 29 (71)
Reguła 30 (86, 135, 149)
Zasada 32 (251)
Zasada 33 (123)
Reguła 34 (48, 187, 243)
Reguła 35 (49, 59, 115)
Zasada 36 (219)
Zasada 37 (91)
Reguła 38 (52, 155, 211)
Reguła 40 (96, 235, 249)
Reguła 41 (97, 107, 121)
Reguła 42 (112, 171, 241)
Zasada 43 (113)
Reguła 44 (100, 203, 217)
Reguła 45 (75, 89, 101)
Reguła 46 (116, 139, 209)
Zasada 50 (179)
Zasada 51
Zasada 54 (147)
Reguła 56 (98, 185, 227)
Zasada 57 (99)
Reguła 58 (114, 163, 177)
Reguła 60 (102, 153, 195)
Reguła 62 (118, 131, 145)
Zasada 72 (237)
Zasada 73 (109)
Reguła 74 (88, 173, 229)
Zasada 76 (205)
Reguła 77
Reguła 78 (92, 141, 197)
Zasada 90 (165)
Zasada 94 (133)
Zasada 104 (233)
Reguła 105
Reguła 106 (120, 169, 225)
Zasada 108 (201)
Reguła 110 (124, 137, 193)
Zasada 122 (161)
Zasada 126 (129)
Zasada 128 (254)
Reguła 130 (144, 190, 246)
Zasada 132 (222)
Reguła 134 (148, 158, 214)
Reguła 136 (192, 238, 252)
Reguła 138 (174, 208, 244)
Reguła 140 (196, 206, 220)
Zasada 142 (212)
Zasada 146 (182)
Reguła 150
Reguła 152 (188, 194, 230)
Reguła 154 (166, 180, 210)
Zasada 156 (198)
Zasada 160 (250)
Reguła 162 (176, 186, 242)
Zasada 164 (218)
Reguła 168 (224, 234, 248)
Zasada 170 (240)
Reguła 172 (202, 216, 228)
Reguła 178
Zasada 184 (226)
Zasada 200 (236)
Reguła 204
Reguła 232

Niezwykłe przypadki

W niektórych przypadkach zachowanie automatu komórkowego nie jest od razu oczywiste. Na przykład w przypadku Reguły 62 struktury oddziałujące rozwijają się jak w klasie 4. Ale w tych interakcjach co najmniej jedna ze struktur zostaje unicestwiona, więc automat ostatecznie wchodzi w stan powtarzalny, a automat komórkowy jest klasy 2.

Zasada 73 jest klasą 2, ponieważ za każdym razem, gdy dwie kolejne jedynki są otoczone zerami, ta cecha jest zachowywana w kolejnych generacjach. To skutecznie tworzy ściany, które blokują przepływ informacji między różnymi częściami tablicy. Istnieje skończona liczba możliwych konfiguracji w sekcji między dwiema ścianami, więc automat musi w końcu zacząć powtarzać się w każdej sekcji, chociaż okres może być bardzo długi, jeśli sekcja jest wystarczająco szeroka. Ściany te utworzą się z prawdopodobieństwem 1 dla całkowicie losowych warunków początkowych. Jeśli jednak zostanie dodany warunek, że długości kolejnych zer lub jedynek muszą być zawsze nieparzyste, to automat będzie zachowywał się w klasie 3, ponieważ ściany nigdy nie mogą się uformować.

Reguła 54 należy do klasy 4 i również wydaje się być zdolna do wykonywania uniwersalnych obliczeń, ale nie została zbadana tak dokładnie jak reguła 110. Skatalogowano wiele oddziałujących na siebie struktur, które łącznie mają być wystarczające dla uniwersalności.

Weisstein, Eric W. „Elementarny automat komórkowy” . MathWorld .
Weisstein, Eric W. „Reguła 30” . MathWorld .
Weisstein, Eric W. „Reguła 50” . MathWorld .
Weisstein, Eric W. „Reguła 54” . MathWorld .
Weisstein, Eric W. „Reguła 60” . MathWorld .
Weisstein, Eric W. „Reguła 62” . MathWorld .
Weisstein, Eric W. „Zasada 90” . MathWorld .
Weisstein, Eric W. „Zasada 94” . MathWorld .
Weisstein, Eric W. „Zasada 102” . MathWorld .
Weisstein, Eric W. „Reguła 110” . MathWorld .
Weisstein, Eric W. „Reguła 126” . MathWorld .
Weisstein, Eric W. „Reguła 150” . MathWorld .
Weisstein, Eric W. „Reguła 158” . MathWorld .
Weisstein, Eric W. „Reguła 182” . MathWorld .
Weisstein, Eric W. „Reguła 188” . MathWorld .
Weisstein, Eric W. „Reguła 190” . MathWorld .
Weisstein, Eric W. „Reguła 220” . MathWorld .
Weisstein, Eric W. „Reguła 222” . MathWorld .

Linki zewnętrzne