hipersympleks

Standardowe hipersimplice w ${\ Displaystyle \ mathbb {R} ^ {3}}$

${\ Displaystyle \ Delta _ {3,1}}$ Hiperpłaszczyzna: ${\ Displaystyle x + y + z = 1}$	${\ Displaystyle \ Delta _ {3,2}}$ Hiperpłaszczyzna: ${\ Displaystyle x + y + z = 2}$

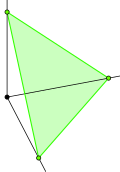
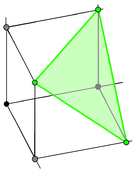
W kombinatoryce $_$ hipersimplex jest wypukłym polytopem , który _ Jest on określony przez dwie liczby całkowite $displaystyle$$jest$ zdefiniowany jako wypukły kadłub wektorów -wymiarowych , $których współczynniki składają$ z $k}$ jedynki i zera ${\ displaystyle dk}$ . $1$ , {d, k}} można uzyskać przez przecięcie jednostki wymiarowej hipersześcianu ${d }}$ ] $\$ { z hiperpłaszczyzną równania ${\ Displaystyle x_ {1} + \ cdots + x_ {d} = k}$$0 <k <d}$$<$ jest to , gdy \

Nieruchomości

Liczba wierzchołków ${\ Displaystyle \ Delta _ {d, k}}$ wynosi ${\ Displaystyle {\ tbinom {d} {k}}}$ . Wykres utworzony przez wierzchołki $}$ hipersimpleksu jest Johnsona. $Displaystyle \ Delta _ {d$ \

Konstrukcje alternatywne

Alternatywną konstrukcją (dla $jest$ wypukłej otoczki wszystkich $Displaystyle (d-1)$ -wymiarowej ${\ Displaystyle (0,1)}$ - wektory, które mają albo ${\ Displaystyle k-1}$ lub ${\ Displaystyle k}$ niezerowe współrzędne. Ma to tę zaletę, że działa w przestrzeni, która ma ten sam wymiar, co wynikowy polytope, ale wadą jest to, że tworzony przez niego polytope jest mniej symetryczny (chociaż kombinatorycznie równoważny wynikowi innej konstrukcji).

Hypersimplex $jest$ również matroidowym polytopem dla jednolitej matroidu z i $rangą$$}$ .

Przykłady

Hypersimplex $re$ -simplex (a zatem ma wierzchołki $-1)$$Displaystyle$ . Hypersimplex $jest$ ośmiościanem $_$ a . _ _ _

$,$ , hypersimplex odpowiada jednolitemu polytope , będąc rektyfikowanym $}$ \ ${\ Displaystyle (d-1)}$ środku wszystkich -wymiarowych ścian a $)}$${\ Displaystyle (d-1)}$ -wymiarowy simplex.

Przykłady (d = 3...6)

Nazwa	Trójkąt równoboczny	Czworościan (3-simplex)	Oktaedr	5-ogniwowy (4-simplex)	Rektyfikowane 5-ogniwowe	5-jednostronny	Rektyfikowany 5-simplex	Birektyfikowany 5-simplex
Δ re , k = ( re , k ) = ( re , re - k )	(3,1) (3,2)	(4,1) (4,3)	(4,2)	(5,1) (5,4)	(5,2) (5,3)	(6,1) (6,5)	(6,2) (6,4)	(6,3)
wierzchołki ${\ Displaystyle {\ tbinom {d} {k}}}$	3	4	6	5	10	6	15	20
d -współrzędne	(0,0,1) (0,1,1)	(0,0,0,1) (0,1,1,1)	(0,0,1,1)	(0,0,0,0,1) (0,1,1,1,1)	(0,0,0,1,1) (0,0,1,1,1)	(0,0,0,0,0,1) (0,1,1,1,1,1)	(0,0,0,0,1,1) (0,0,1,1,1,1)	(0,0,0,1,1,1)
Obraz
Wykresy	J (3,1) = K 2	J (4,1) = K 3	J (4,2) = T(6,3)	J (5,1) = K 4	J (5,2)	J (6,1) = K. 5	J. (6,2)	J (6,3)
Diagramy Coxetera
symbole Schläfliego	{3} = r {3}	{3,3} = 2 r {3,3}	r{3,3} = {3,4}	{3,3,3} = 3r { 3,3,3}	r {3,3,3} = 2 r { 3,3,3}	{3,3,3,3} = 4 r {3,3,3,3}	r {3,3,3,3} = 3 r {3,3,3,3}	2r { 3,3,3,3 }
aspekty	{}	{3}		{3,3}	{3,3}, {3,4}	{3,3,3}	{3,3,3}, r {3,3,3}	r {3,3,3}

Historia

Hipersimplice zostały po raz pierwszy zbadane i nazwane w obliczeniach klas charakterystycznych (ważny temat w topologii algebraicznej ) przez Gabrièlova, Gelfanda i Losika (1975) .

Dalsza lektura

• Hibi, Takayuki; Solus, Liam (2016), „Aspekty r -stabilnej (n , k) -hypersimplex”, Annals of Combinatorics , 20 : 815–829, arXiv : 1408,5932 , Bibcode : 2014arXiv1408.5932H , doi : 10.1007/s00026-016 -0325-x .