Wykres Johnsona

Wykres Johnsona
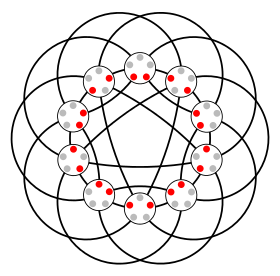Wykres Johnsona J (5,2)
Nazwany po	Selmera M. Johnsona
Wierzchołki	${\ Displaystyle {\ binom {n} {k}}}$
Krawędzie	${\ Displaystyle {\ Frac {1} {2}} k (nk) {\ binom {n} {k}}}$
Średnica	${\ Displaystyle \ min (k, nk)}$
Nieruchomości	${\ Displaystyle k (nk)}$ -regularny Vertex-przechodni Odległość-przechodnia Hamilton-connected
Notacja	${\ Displaystyle J (n, k)}$
Tabela wykresów i parametrów

Grafy Johnsona to specjalna klasa grafów nieskierowanych zdefiniowanych na podstawie systemów zbiorów. Wierzchołki $n$$displaystyle$ -elementowe podzbiory $}$ \ dwa wierzchołki sąsiadują ze sobą, gdy przecięcie dwóch wierzchołków (podzbiorów) zawiera elementy ${\ Displaystyle (k-1)} .$ Zarówno wykresy Johnsona, jak i blisko spokrewnione Program Johnsona został nazwany na cześć Selmera M. Johnsona .

Przypadki specjalne

• ${\ Displaystyle J (n, 1)}$ to kompletny wykres K _n .
• ${\ Displaystyle J (4,2)}$ jest wykresem ośmiościennym .
• ${\ Displaystyle J (5,2)}$ jest wykresem dopełnienia wykresu Petersena , stąd wykres liniowy K ₅ . $2$ , dla $wykres$ Johnsona wykresu ${\ Displaystyle K (n, 2).}$

Własności teoretyczne grafów

• ${\ Displaystyle J (n, k)}$ jest izomorficzny z ${\ Displaystyle J (n, nk).}$

• Dla wszystkich ${\ Displaystyle 0 \ równoważnik j \ równoważnik \ nazwa operatora {średnica} (J (n, k))}$ , dowolna para wierzchołków w odległości dzieli ${\ displaystyle j}$${\ displaystyle kj}$ wspólne elementy.

• $,$ spójny Hamiltona co oznacza, para wierzchołków tworzy punkty końcowe Hamiltona na W szczególności oznacza to, że ma cykl Hamiltona.

• Wiadomo również, że wykres Johnsona ( $Displaystyle J (n,$${\ Displaystyle ~ k (nk)}$ -połączony z wierzchołkami.

• ${\ Displaystyle J (n, k)}$ tworzy wykres wierzchołków i krawędzi ( n - 1) -wymiarowego polytope , zwanego hipersimplexem .

• liczba kliki $jest$ dana wyrażeniem w postaci $}} {\ lambda _ {\ min}}}.}$ i

• Liczba chromatyczna J ${\ Displaystyle J (n, k)}$ jest co najwyżej ${\ Displaystyle n, \ chi (J (n, k)) \ równoważnik n.}$

Grupa automorfizmów

Istnieje podgrupa przechodnia odległości ${\ Displaystyle \ operatorname {Aut} (J (n, k)}}$ izomorficzna z ${\ Displaystyle \ operatorname {Sym} (n)}$ . Faktycznie ${\ Displaystyle \ nazwa operatora {Aut} (J (n, k)) \ kong \ nazwa operatora {Sym} (n)}$ , chyba że ${\ Displaystyle n = 2k \ geq 4}$ ; w przeciwnym razie ${\ Displaystyle \ nazwa operatora {Aut} (J (n, k)} \ kong \ nazwa operatora {Sym} (n) \ razy C_ {2}}$ .

Tablica przecięć

W konsekwencji bycia przechodnim $na$ odległość na Pozwalając $średnicy$ , tablica przecięć jest dana przez ${\ Displaystyle J (n, k)}$

${\ Displaystyle \ lewo \ {b_ {0}, \ ldots, b_ {d-1}, c_ {1}, \ ldots c_ {d} \Prawidłowy\}}$

Gdzie:

$b_ {j} & = (kj) (nkj) & & 0 \leq j<d\\c_{j}&=j^{2}&&0<j\leq d\end{wyrównane}}}$

$nie$ się, że jeśli nie $współdzielona$ tablica z -regularny wykres; tablica przecięć $jest$ z trzema innymi wykresami odległości regularnymi, które

Wartości własne i wektory własne

• Charakterystyczny przez $k$

${\ Displaystyle \ phi (x): = \ prod _ {j = 0} ^ {\ nazwa operatora {diam} (J (n, k))} \ lewo (xA_ {n, k} (j) \ prawo ) ^ {{\binom {n}{j}}-{\binom {n}{j-1}}}.}$

gdzie ${\ Displaystyle A_ {n, k} (j) = (kj) (nkj) -j.}$

• Wektory własne jot $\ Displaystyle J (n, k)}$ mieć wyraźny opis.

schemat Johnsona

Wykres Johnsona $( n , k ) {\ Displaystyle J (n$ ściśle powiązany ze schematem Johnsona , schematem skojarzeń , w którym każda para zestawów elementów k jest powiązana z liczbą o połowę mniejszą od symetryczna różnica obu zbiorów. Wykres Johnsona ma krawędź dla każdej pary zbiorów w odległości 1 w schemacie asocjacji, a odległości w schemacie asocjacji są dokładnie najkrótszymi odległościami ścieżek na grafie Johnsona.

$}$ odległość, nieparzystymi , których wierzchołki są -elementu $displaystyle k$ { \ zbiór i którego krawędzie odpowiadają rozłącznym parom podzbiorów.

Otwarte problemy

Właściwości rozszerzania wierzchołków grafów Johnsona, a także struktura odpowiadających im ekstremalnych zbiorów wierzchołków o danym rozmiarze, nie są w pełni zrozumiałe. Jednak ostatnio uzyskano asymptotycznie ścisłe dolne ograniczenie ekspansji dużych zbiorów wierzchołków.

Ogólnie rzecz biorąc, określenie liczby chromatycznej wykresu Johnsona jest problemem otwartym.

Zobacz też

• Wykres Grassmanna

Linki zewnętrzne

• Weisstein, Eric W. „Wykres Johnsona” . MathWorld .
• Brouwer, Andries E. „Wykresy Johnsona” .