postać normalna Chomsky'ego

W formalnej teorii języka mówi się, że gramatyka bezkontekstowa G jest w postaci normalnej Chomsky'ego (po raz pierwszy opisana przez Noama Chomsky'ego ), jeśli wszystkie jej reguły produkcji mają postać:

ZA → BC , lub

ZA → a , lub

S → ε,

gdzie A , B i C są symbolami nieterminalnymi , litera a jest symbolem końcowym (symbolem reprezentującym stałą wartość), S jest symbolem początkowym, a ε oznacza pusty ciąg znaków . Ponadto ani B, ani C nie mogą być symbolem początkowym , a trzecia reguła produkcji może pojawić się tylko wtedy, gdy ε jest w L ( G ), języku tworzonym przez gramatykę bezkontekstową G .

Każda gramatyka w postaci normalnej Chomsky'ego jest bezkontekstowa i odwrotnie, każdą gramatykę bezkontekstową można przekształcić w równoważną gramatykę, która jest w postaci normalnej Chomsky'ego i ma rozmiar nie większy niż kwadrat rozmiaru oryginalnej gramatyki.

Konwersja gramatyki do postaci normalnej Chomsky'ego

Aby przekształcić gramatykę do postaci normalnej Chomsky'ego, stosuje się sekwencję prostych przekształceń w określonej kolejności; jest to opisane w większości podręczników teorii automatów . Prezentacja jest następująca po Hopcroft, Ullman (1979), ale jest przystosowana do używania nazw transformacji z Lange, Leiß (2009). Każda z poniższych transformacji ustanawia jedną z właściwości wymaganych dla postaci normalnej Chomsky'ego.

START: Usuń symbol startu z prawej strony

₀ Wprowadź nowy symbol startu S i nową regułę

₀ S → S ,

₀ gdzie S to poprzedni symbol startu. Nie zmienia to tworzonego języka gramatyki, a S nie pojawi się po prawej stronie żadnej reguły.

TERM: Wyeliminuj reguły za pomocą niesamotnych terminali

Aby wyeliminować każdą regułę

ZA → X ₁ ... za ... X _n

gdzie symbol terminala a nie _jest jedynym symbolem po prawej stronie, wprowadź dla każdego takiego terminala nowy symbol nieterminalny Na i nową regułę

N _za → za .

Zmień każdą regułę

ZA → X ₁ ... za ... X _n

Do

ZA → X ₁ ... Na _za ... X _n .

Jeśli po prawej stronie występuje kilka symboli terminali, jednocześnie zastąp każdy z nich odpowiednim symbolem nieterminalnym. Nie zmienia to języka produkowanego przez gramatykę.

BIN: Wyeliminuj prawą stronę z więcej niż 2 nieterminalami

Zastąp każdą regułę

ZA → X ₁ X ₂ ... X _rz

z więcej niż 2 nieterminalami X ₁ ,..., X _n według reguł

ZA → X ₁ ZA ₁ ,

ZA ₁ → X ₂ ZA ₂ ,

... ,

ZA _{n -2} → X _{n -1} X _n ,

gdzie A _i to nowe symbole nieterminalne. Ponownie, nie zmienia to języka produkowanego przez gramatykę.

DEL: Wyeliminuj reguły ε

Reguła ε jest regułą formy

A → ε,

₀ gdzie A nie jest S , symbolem początku gramatyki.

Aby wyeliminować wszystkie reguły tej postaci, najpierw określ zbiór wszystkich nieterminali wyprowadzających ε. Hopcroft i Ullman (1979) nazywają takie nieterminale nullable i obliczają je w następujący sposób:

Jeśli istnieje reguła A → ε, to A jest zerowalna.
Jeśli istnieje reguła A → X ₁ ... X _n i każdy pojedynczy X _i jest zerowalny, to A również jest zerowalny.

Uzyskaj gramatykę pośrednią, zastępując każdą regułę

ZA → X ₁ ... X _rz

przez wszystkie wersje z niektórymi zerowanymi X _i pominiętymi. Usuwając w tej gramatyce każdą regułę ε, o ile jej lewa strona nie jest symbolem startu, uzyskuje się przekształconą gramatykę.

₀ Na przykład w poniższej gramatyce z symbolem początku S ,

₀ S → AbB | C

B → AA | AC

C → b | c

ZA → za | ε

₀ nieterminal A , a zatem także B , dopuszcza wartość null, podczas gdy ani C , ani S nie są. W ten sposób uzyskuje się następującą gramatykę pośrednią:

₀ S → A b B | A b B | A b B | A b B | C

B → AA | A A | A A | ZA ε A | C _ | ZA C

C → b | c

ZA → za | ε

W tej gramatyce wszystkie reguły ε zostały „ wstawione w miejscu wywołania”. W następnym kroku można je zatem usunąć, otrzymując gramatykę:

₀ S → AbB | Ab | bB | b | C

B → AA | | _ AC | C

do → b | c

A → a

Ta gramatyka tworzy ten sam język, co oryginalna gramatyka przykładowa, a mianowicie. { ab , aba , abaa , abab , abac , abb , abc , b , bab , bac , bb , bc , c }, ale nie ma reguł ε.

JEDNOSTKA: Wyeliminuj zasady dotyczące jednostek

Reguła jednostkowa jest regułą formy

A → B ,

gdzie A , B są symbolami nieterminalnymi. Aby go usunąć, dla każdej reguły

B → X ₁ ... X _n ,

gdzie X ₁ ... X _n to ciąg nieterminali i terminali, dodaj regułę

ZA → X ₁ ... X _rz

chyba że jest to reguła jednostki, która została już (lub jest w trakcie) usuwana. Pominięcie symbolu nieterminalnego B w wynikowej gramatyce jest możliwe, ponieważ B jest członkiem domknięcia jednostkowego symbolu nieterminalnego A .

Kolejność przekształceń

Wzajemne zachowanie wyników transformacji
Y X	POCZĄTEK	TERMIN	KOSZ	DEL	JEDNOSTKA
Transformacja X zawsze zachowuje ( Y ) wzgl. może zniszczyć ( N ) wynik Y :
ROZPOCZNIJ
TERMIN
KAS
. USUW
JEDNOSTKA				( T ) ^*
^* UNIT zachowuje wynik DEL , jeśli wcześniej wywołano START .

Wybierając kolejność, w jakiej mają być stosowane powyższe przekształcenia, należy wziąć pod uwagę, że niektóre przekształcenia mogą zniweczyć wynik osiągnięty przez inne. Na przykład START ponownie wprowadzi regułę jednostki, jeśli zostanie zastosowana po UNIT . Tabela pokazuje, które zamówienia są dopuszczone.

Co więcej, najgorsze rozdęcie w rozmiarze gramatyki zależy od kolejności transformacji. Używanie | G | aby określić rozmiar oryginalnej gramatyki G , powiększenie rozmiaru w najgorszym przypadku może wahać się od | G | ² do 2 ^{2 |G|} , w zależności od zastosowanego algorytmu transformacji. Powiększenie rozmiaru gramatyki zależy od kolejności między DEL i BIN . Może być wykładniczy, gdy DEL jest wykonywany jako pierwszy, ale w przeciwnym razie jest liniowy. JEDNOSTKA może wywołać kwadratowe powiększenie wielkości gramatyki. Porządki START , TERM , BIN , DEL , UNIT i START , BIN , DEL , UNIT , TERM prowadzą do najmniejszego (tj. kwadratowego) powiększenia.

Przykład

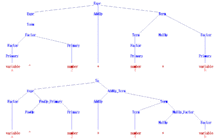
Abstrakcyjne drzewo składniowe wyrażenia arytmetycznego " a ^2+4* b " wrt. przykładowa gramatyka ( na górze ) i jej postać normalna Chomsky'ego ( na dole )

Poniższa gramatyka, z symbolem początkowym Expr , opisuje uproszczoną wersję zestawu wszystkich składniowych poprawnych wyrażeń arytmetycznych w językach programowania, takich jak C lub Algol60 . Dla uproszczenia zarówno liczba , jak i zmienna są uważane za symbole końcowe, ponieważ w interfejsie kompilatora ich wewnętrzna struktura zwykle nie jest uwzględniana przez parser . Symbol końcowy „^” oznaczał potęgowanie w Algol60.

Wyr	→ Termin	\| Termin AddOp Expr	\| Termin AddOp
Termin	→ Współczynnik	\| Terminowy współczynnik MulOp
Czynnik	→ Podstawowy	\| Czynnik ^ Podstawowy
Podstawowy	→ liczba	\| zmienny	\| ( Wyr )
Dodaj op	→ +	\| −
MulOp	→ *	\| /

₀ W kroku „START” powyższego algorytmu konwersji do gramatyki dodawana jest tylko reguła S → Wyr . Po kroku „TERM” gramatyka wygląda następująco:

S₀	→ Wyr
Wyr	→ Termin	\| Termin AddOp Expr	\| Termin AddOp
Termin	→ Współczynnik	\| Terminowy współczynnik MulOp
Czynnik	→ Podstawowy	\| Czynnik PowOp podstawowy
Podstawowy	→ liczba	\| zmienny	\| Otwórz Eksr Zamknij
Dodaj op	→ +	\| −
MulOp	→ *	\| /
PowOp	→ ^
otwarty	→ (
Zamknąć	→ )

Po kroku „BIN” uzyskuje się następującą gramatykę:

S₀	→ Wyr
Wyr	→ Termin	\| Wyr AddOp_Term	\| Termin AddOp
Termin	→ Współczynnik	\| Termin MulOp_Factor
Czynnik	→ Podstawowy	\| Czynnik PowOp_Primary
Podstawowy	→ liczba	\| zmienny	\| Otwórz Expr_Close
Dodaj op	→ +	\| −
MulOp	→ *	\| /
PowOp	→ ^
otwarty	→ (
Zamknąć	→ )
AddOp_Term	→ Dodaj termin Op
MulOp_Factor	→ Współczynnik MulOp
PowOp_Podstawowy	→ Podstawowy PowOp
Wyr_Zamknij	→ Wyr Zamknij

Ponieważ nie ma reguł ε, krok „DEL” nie zmienia gramatyki. Po kroku „JEDNOSTKA” uzyskuje się następującą gramatykę, która jest w postaci normalnej Chomsky'ego:

S₀	→ liczba	\| zmienny	\| Otwórz Expr_Close	\| Czynnik PowOp_Primary	\| Termin MulOp_Factor	\| Wyr AddOp_Term	\| Termin AddOp
Wyr	→ liczba	\| zmienny	\| Otwórz Expr_Close	\| Czynnik PowOp_Primary	\| Termin MulOp_Factor	\| Wyr AddOp_Term	\| Termin AddOp
Termin	→ liczba	\| zmienny	\| Otwórz Expr_Close	\| Czynnik PowOp_Primary	\| Termin MulOp_Factor
Czynnik	→ liczba	\| zmienny	\| Otwórz Expr_Close	\| Czynnik PowOp_Primary
Podstawowy	→ liczba	\| zmienny	\| Otwórz Expr_Close
Dodaj op	→ +	\| −
MulOp	→ *	\| /
PowOp	→ ^
otwarty	→ (
Zamknąć	→ )
AddOp_Term	→ Dodaj termin Op
MulOp_Factor	→ Współczynnik MulOp
PowOp_Podstawowy	→ Podstawowy PowOp
Wyr_Zamknij	→ Wyr Zamknij

Na _wprowadzone w kroku „TERM” to PowOp , Open i Close . Ai wprowadzone w kroku „BIN” to AddOp_Term , MulOp_Factor , _{PowOp_Primary} i Expr_Close .

Alternatywna definicja

zredukowana forma Chomsky'ego

Innym sposobem zdefiniowania postaci normalnej Chomsky'ego jest:

Gramatyka formalna jest w postaci zredukowanej Chomsky'ego, jeśli wszystkie jej reguły produkcji mają postać:

{\ Displaystyle A \ rightarrow \, pne}

lub

{\ Displaystyle A \ rightarrow \, a}

,

gdzie są symbolami nieterminalnymi, a symbolami terminalnymi są ZA $displaystyle A}$ \ $\ displaystyle$ $B$ $}$ Podczas korzystania z tej definicji symbolem początkowym może być ${\ displaystyle B}$ ${\ displaystyle C} .$ do Tylko te gramatyki bezkontekstowe, które nie generują pustego łańcucha, można przekształcić w postać zredukowaną Chomsky'ego.

postać normalna Floyda

W liście, w którym zaproponował termin Forma Backusa – Naura (BNF), Donald E. Knuth zasugerował „składnię BNF, w której można powiedzieć, że wszystkie definicje mają taką formę w„ postaci normalnej Floyda ””

{\ Displaystyle \ langle A \ rangle :: = \ \ langle B \ rangle \ mid \ langle C \ rangle}

lub

{\ Displaystyle \ langle A \ rangle :: = \, \ langle B \ rangle \ langle C \ rangle}

lub

{\ Displaystyle \ langle A \ rangle :: = \, a

}

gdzie ${\ Displaystyle \ langle A \ rangle}$ , ${\ Displaystyle \ langle B \ rangle}$ i ${\ Displaystyle \ langle C \ rangle}$ symbolami nieterminalnymi i ${\ Displaystyle a}$ jest symbolem końcowym, ponieważ Robert W. Floyd odkrył, że każdą składnię BNF można przekonwertować na powyższą w 1961 roku. Wycofał jednak ten termin, „ponieważ bez wątpienia wielu ludzi niezależnie wykorzystało ten prosty fakt w swojej własnej pracy, a chodzi o to tylko przypadkowe w stosunku do głównych rozważań notatki Floyda”. Podczas gdy notatka Floyda cytuje oryginalny artykuł Chomsky'ego z 1959 roku, list Knutha nie.

Aplikacja

Oprócz swojego teoretycznego znaczenia, konwersja CNF jest wykorzystywana w niektórych algorytmach jako etap wstępnego przetwarzania, np. algorytm CYK , parsowanie oddolne dla gramatyk bezkontekstowych i jego wariant probabilistyczny CKY.

Zobacz też

Forma Backusa-Naura
Algorytm CYK
postać normalna Greibacha
Normalna postać Kurody
Lemat o pompowaniu dla języków bezkontekstowych — jego dowód opiera się na postaci normalnej Chomsky'ego

Notatki

^ Chomsky, Noam (1959). „O niektórych formalnych właściwościach gramatyk” . Informacji i Kontroli . 2 (2): 137–167. doi : 10.1016/S0019-9958(59)90362-6 . Tutaj: Sekcja 6, s. 152ff.
Bibliografia _ „Strona 7, wykład 9: algorytmy analizy oddolnej” (PDF) . CS536-S21 Wprowadzenie do języków programowania i kompilatorów . Uniwersytet Wisconsin-Madison. Zarchiwizowane (PDF) od oryginału w dniu 2021-07-19.
^ Sipser, Michael (2006). Wprowadzenie do teorii obliczeń (wyd. 2). Boston: technologia kursu Thomsona. Definicja 2.8. ISBN 0-534-95097-3 . OCLC 58544333 .
^ ^a ^b ^c ^d ^e ^f Hopcroft, John E.; Ullman, Jeffrey D. (1979). Wprowadzenie do teorii automatów, języków i obliczeń . Reading, Massachusetts: Wydawnictwo Addison-Wesley. ISBN 978-0-201-02988-8 .
Bibliografia _ Motwani, Rajeev; Ullman, Jeffrey D. (2006). Wprowadzenie do teorii automatów, języków i obliczeń (wyd. 3). Addison-Wesley. ISBN 978-0-321-45536-9 . Sekcja 7.1.5, s. 272
^ Bogaty, Elaine (2007). „11.8 Formy normalne”. Automaty, obliczalność i złożoność: teoria i zastosowania (wyd. 1). Prentice Hall. P. 169. ISBN 978-0132288064 . Zarchiwizowane od oryginału (PDF) w dniu 16.01.2022.
^ Wegener, Ingo (1993). Theoretische Informatik - Eine algorytmenorientierte Einführung . Leitfäden und Mongraphien der Informatik (w języku niemieckim). Stuttgart: BG Teubner. ISBN 978-3-519-02123-0 . Sekcja 6.2 „Die Chomsky-Normalform für contextfreie Grammatiken”, s. 149–152
^; ^ ^abc ^Lange , Martin Leiß, Hans (2009). „Do CNF czy nie do CNF? Wydajna, ale prezentowalna wersja algorytmu CYK” (PDF) . Dydaktyka Informatyki . 8 . Zarchiwizowane (PDF) od oryginału w dniu 19.07.2011.
^ Allison, Charles D. (2022). Podstawy informatyki: dostępne wprowadzenie do automatów i języków formalnych . Świeże źródła, Inc. str. 176. ISBN 9780578944173 .
Bibliografia _ (2006) ^{[ potrzebna strona ]}
^ Floyd, Robert W. (1961). „Uwaga na temat indukcji matematycznej w gramatyce struktur frazowych” (PDF) . Informacji i Kontroli . 4 (4): 353–358. doi : 10.1016/S0019-9958(61)80052-1 . Zarchiwizowane (PDF) od oryginału w dniu 05.03.2021 r. Tutaj: s.354
^ Knuth, Donald E. (grudzień 1964). „Postać normalna Backus kontra forma Backus Naur”. Komunikaty ACM . 7 (12): 735–736. doi : 10.1145/355588.365140 . S2CID 47537431 .
^ Jurajski, Daniel; Martin, James H. (2008). Przetwarzanie mowy i języka (wyd. 2). Pearson Prentice Hall. P. 465. ISBN 978-0-13-187321-6 .

Dalsza lektura

Kol, Ryszard. Konwersja CFG do CNF (Chomsky Normal Form) , 17 października 2007 r. (pdf) — używa kolejności TERM, BIN, START, DEL, UNIT.
Johna Martina (2003). Wprowadzenie do języków i teorii obliczeń . Wzgórze McGrawa. ISBN 978-0-07-232200-2 . (Strony 237–240 sekcji 6.6: formularze uproszczone i formularze zwykłe).
Michaela Sipsera (1997). Wprowadzenie do teorii obliczeń . Wydawnictwo PWS. ISBN 978-0-534-94728-6 . (Strony 98–101 sekcji 2.1: gramatyki bezkontekstowe. Strona 156.)
Charles D.Allison (2021) (20 sierpnia 2021). Podstawy informatyki: dostępne wprowadzenie do języka formalnego . Świeże źródła, Inc. ISBN 9780578944173 . (strony 171-183 sekcji 7.1: Postać normalna Chomsky'ego)
Sipser, Michał. Wprowadzenie do teorii obliczeń, wydanie 2.
Aleksander Meduna (6 grudnia 2012). Automaty i języki: teoria i zastosowania . Springer Science & Business Media. ISBN 978-1-4471-0501-5 .

[1] Chomsky, Noam (1959). „O niektórych formalnych właściwościach gramatyk” . Informacji i Kontroli . 2 (2): 137–167. doi : 10.1016/S0019-9958(59)90362-6 . Tutaj: Sekcja 6, s. 152ff.

[2] Bibliografia _ „Strona 7, wykład 9: algorytmy analizy oddolnej” (PDF) . CS536-S21 Wprowadzenie do języków programowania i kompilatorów . Uniwersytet Wisconsin-Madison. Zarchiwizowane (PDF) od oryginału w dniu 2021-07-19.

[3] Sipser, Michael (2006). Wprowadzenie do teorii obliczeń (wyd. 2). Boston: technologia kursu Thomsona. Definicja 2.8. ISBN 0-534-95097-3 . OCLC 58544333 .

[Hopcroft.Ullman.1979-4] ^ ^a ^b ^c ^d ^e ^f Hopcroft, John E.; Ullman, Jeffrey D. (1979). Wprowadzenie do teorii automatów, języków i obliczeń . Reading, Massachusetts: Wydawnictwo Addison-Wesley. ISBN 978-0-201-02988-8 .

[6] Bibliografia _ Motwani, Rajeev; Ullman, Jeffrey D. (2006). Wprowadzenie do teorii automatów, języków i obliczeń (wyd. 3). Addison-Wesley. ISBN 978-0-321-45536-9 . Sekcja 7.1.5, s. 272

[7] Bogaty, Elaine (2007). „11.8 Formy normalne”. Automaty, obliczalność i złożoność: teoria i zastosowania (wyd. 1). Prentice Hall. P. 169. ISBN 978-0132288064 . Zarchiwizowane od oryginału (PDF) w dniu 16.01.2022.

[8] Wegener, Ingo (1993). Theoretische Informatik - Eine algorytmenorientierte Einführung . Leitfäden und Mongraphien der Informatik (w języku niemieckim). Stuttgart: BG Teubner. ISBN 978-3-519-02123-0 . Sekcja 6.2 „Die Chomsky-Normalform für contextfreie Grammatiken”, s. 149–152

[Lange.Leis.2009-9] ; ^ ^abc ^Lange , Martin Leiß, Hans (2009). „Do CNF czy nie do CNF? Wydajna, ale prezentowalna wersja algorytmu CYK” (PDF) . Dydaktyka Informatyki . 8 . Zarchiwizowane (PDF) od oryginału w dniu 19.07.2011.

[13] Allison, Charles D. (2022). Podstawy informatyki: dostępne wprowadzenie do automatów i języków formalnych . Świeże źródła, Inc. str. 176. ISBN 9780578944173 .

[15] Bibliografia _ (2006) ^{[ potrzebna strona ]}

[16] Floyd, Robert W. (1961). „Uwaga na temat indukcji matematycznej w gramatyce struktur frazowych” (PDF) . Informacji i Kontroli . 4 (4): 353–358. doi : 10.1016/S0019-9958(61)80052-1 . Zarchiwizowane (PDF) od oryginału w dniu 05.03.2021 r. Tutaj: s.354

[knuth1964-17] Knuth, Donald E. (grudzień 1964). „Postać normalna Backus kontra forma Backus Naur”. Komunikaty ACM . 7 (12): 735–736. doi : 10.1145/355588.365140 . S2CID 47537431 .

[18] Jurajski, Daniel; Martin, James H. (2008). Przetwarzanie mowy i języka (wyd. 2). Pearson Prentice Hall. P. 465. ISBN 978-0-13-187321-6 .