włóknienie Kana

W matematyce kompleksy Kan i fibracje Kan są częścią teorii zbiorów uproszczonych . Fibracje Kan są fibracjami kategorii modelu standardowego na zbiorach uproszczonych i dlatego mają fundamentalne znaczenie. Obiektami fibrantowymi w tej kategorii modeli są kompleksy Kan . Nazwa jest na cześć Daniela Kana .

Definicje

Definicja standardowego n-simpleksu

Pasiasty niebieski simpleks w domenie musi istnieć, aby ta mapa była włóknieniem Kan

$możliwym$ standardowy -simplex że dla każdego n ≥ 0 , jest do przedstawienia zbiorem uproszczonym ${\ Displaystyle \ Delta ^ {n}}$

${\ Displaystyle \ Delta ^ {n} (i) = \ operatorname {Hom} _ {\ mathbf {\ Delta}} ([i] ,[N])}$

Zastosowanie geometrycznego funktora realizacji do tego zbioru uproszczonego daje przestrzeń homeomorficzną ze $-simpleks :$ topologicznym n ${\ displaystyle ( t_{0},\dots ,t_{n})}$ podprzestrzeń ℝ ^{n + 1} składająca się ze wszystkich punktów takie, że współrzędne są nieujemne i sumują się do 1.

Definicja rogu

Główny artykuł: Róg simplexu

Dla każdego k ≤ n $^ {n}$ ma to podzespół , k -ty róg wewnątrz , odpowiadający $_ {k}$ granica n -simpleksu, z usuniętą k -tą ścianą. Można to formalnie zdefiniować na różne sposoby, jak na przykład suma obrazów n map ${\ Displaystyle \ Delta ^ {n-1} \ rightarrow \ Delta ^ {n}}$ odpowiadające wszystkim innym ścianom ${\ Displaystyle \ Delta ^ {n}}$ . Rogi postaci siedzącej wewnątrz $góry$ czarne V $.$ Jeśli jest $zbiorem$ , to mapuje

${\ Displaystyle s: \ Lambda _ {k} ^ {n} \ do X}$

odpowiadają zbiorom ${\ Displaystyle n}$${\ Displaystyle (n-1)}$ -simplices spełniające warunek zgodności, po jednym dla każdego ${\ Displaystyle 0 \ równoważnik k \ równoważnik n -1}$ . Jawnie warunek ten można zapisać w następujący sposób. $(n-1)}$ Displaystyle -simplices jako listę ${\ Displaystyle (s_ {0}, \ kropki, s_ {k-1}, s_ {k + 1}, \ kropki, s_ {n})$ }

$\ Displaystyle d_ {i} s_ {j} = d_ {j-1} s_ {i} \,}$ dla wszystkich ${\ Displaystyle i <j}$ z ${\ Displaystyle i, j \ neq k$ .

Warunki te są spełnione dla siedzącego wewnątrz Λ $\$$Displaystyle \ Lambda _ {k} ^ {n}}$$^ {n.}}$ .

Definicja włóknienia Kan

Schemat podnoszenia dla rozwłóknienia Kan

Mapa zbiorów uproszczonych $,$ włóknieniem Kan $dowolnego$ dla $n$, and for any maps $s:\Lambda _{k}^{n}\rightarrow X$ and ${\ Displaystyle y: \ Delta ^ {n} \ rightarrow Y \}$ takie, że ${\ Displaystyle f \ circ s = y \ circ i}$ (gdzie ${\ displaystyle i}$ jest inkluzją Λ ${\ Displaystyle \ Lambda _ {k} ^ {n}}$ w ${\ Displaystyle \ Delta ^ {n}} )$ mapa ${\ Displaystyle x: \ Delta ^{n}\rightarrow X}$ takie, że ${\ Displaystyle s = x \ circ i}$ i ${\ Displaystyle y = f \ circ x}$ . Ujmując to w ten sposób, definicja jest bardzo podobna do definicji fibracji w topologii (patrz także właściwość podnoszenia homotopii ), stąd nazwa „fibracja”.

Uwagi techniczne

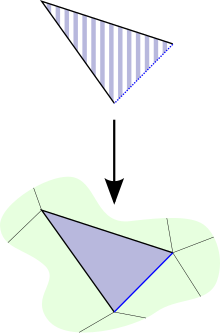
Używając zgodności między $zbioru$ uproszczonego i morfizmami ${\$$Displaystyle \ Delta ^ {n} \ do X}$ (konsekwencja lematu Yoneda , tę definicję można zapisać w postaci uproszczeń. $powyżej$ mapy traktować Pytanie o ${\ displaystyle fs}$ czynniki przez ${\ displaystyle yi}$ odpowiada wymaganiu, aby istniał $displaystyle$ w $Y}$ , którego twarze tworzą róg od ${\ displaystyle fs}$ (wraz z jeszcze jedną twarzą). Wtedy wymagana mapa odpowiada simpleksowi w $: \ Delta ^ {n} \ do$$X}$ których twarze obejmują róg z ${\ displaystyle s}$ . Diagram po prawej stronie jest przykładem w dwóch wymiarach. Ponieważ czarne V na dolnym diagramie jest wypełnione przez niebieski $-simplex$ , jeśli czarne V powyżej jest do niego odwzorowywane, to niebieski w paski $istnieć$ wraz z niebieski w $-$ simplex, odwzorowujący w oczywisty sposób.

Kompleksy Kan zdefiniowane na podstawie fibracji Kan

Zbiór uproszczony $,$$włóknieniem$ kompleksem Kan z jednopunktowego zbioru uproszczonego jest W kategorii modeli dla zbiorów uproszczonych $jest$ obiektem końcowym, więc kompleks Kan jest dokładnie tym samym, . Równoważnie można to wyrazić następująco: jeśli każda mapa $\ do X}$$:$${\ Displaystyle {\ tylda {\ alfa}}: \ Delta ^ {n} \ do X}$ z klaksonu ma rozszerzenie do , co oznacza, że ​​​​jest winda takie, że

${\ Displaystyle \ alfa = {\ tylda {\ alfa}} \ circ \ jota}$

$_$ mapy _ $_$ _ I odwrotnie, każdy kompleks Kan ma tę właściwość, stąd daje prosty warunek techniczny dla kompleksu Kan.

Przykłady

Zbiory uproszczone z homologii osobliwej

Ważny przykład pochodzi z konstrukcji pojedynczych uproszczeń używanych do definiowania osobliwej homologii , zwanej funktorem osobliwym ^{pg 7}

${\ Displaystyle S: {\ tekst {Góra}} \ do s {\ tekst {Zestawy}}}$ .

Biorąc pod uwagę przestrzeń , zdefiniuj $}$ pojedynczą -simplex X jako ciągłą mapę od standardowej topologii $\ displaystyle n}$ (jak opisano powyżej) do X { $X$$X}$$displaystyle n$ ,

${\ Displaystyle f: \ Delta _ {n} \ do X}$

Biorąc zestaw tych map dla wszystkich nieujemnych, daje zestaw stopniowany, ${\ displaystyle n}$

${\ Displaystyle S (X) = \ coprod _ {n} S_ {n} (X)}$ .

Aby uczynić to uproszczonym zestawem, zdefiniuj mapy twarzy ${\ Displaystyle d_ {i}: S_ {n} (X) \ do S_ {n-1} (X)}$ wg

${\ Displaystyle (d_ {i} f) (t_ {0},\kropki,t_{n-1})=f(t_{0},\kropki,t_{i-1},0,t_{i},\kropki,t_{n-1})\ ,}$

i mapy degeneracji ${\ Displaystyle s_ {i}: S_ {n} (X) \ do S_ {n + 1} (X)}$ przez

${\ Displaystyle (s_ {i} f) (t_ {0}, \ kropki, t_ {n + 1}) = f (t_ {0}, \ kropki, t_ {i-1}, t_ {i} + t_ {i+1},t_{i+2},\kropki,t_{n+1})\,}$ .

Ponieważ połączenie dowolnych ścian $Displaystyle \ Delta _ {n + 1}}$${\$ silnym wycofaniem deformacji $}} ,$$Delta _ { n +$$}$$\ Displaystyle S (X)$ można rozszerzyć do , co pokazuje, że jest kompleksem Kan.

Związek z realizacją geometryczną

Warto zauważyć, że funktor liczby pojedynczej jest ściśle przylegający do funktora realizacji geometrycznej

${\ Displaystyle |\ cdot |: s {\ tekst {Zestawy}} \ do {\ tekst {Top}}}$

podając izomorfizm

${\ Displaystyle {\ tekst {Hom}} _ {\ tekst {Top}} (| X |, Y) \ cong {\ text{Hom}}_{s{\text{Zestawy}}}(X,S(Y))}$

Zestawy uproszczone leżące u podstaw grup uproszczonych

Można wykazać, że zbiór uproszczony leżący u podstaw grupy uproszczonej jest zawsze fibrant ^{pg 12} . W szczególności dla uproszczonej grupy abelowej jej realizacja geometryczna jest homotopią równoważną iloczynowi przestrzeni Eilenberga-Maclane'a

${\ Displaystyle \ prod _ {i \ w ja} K (A_ {i}, n_ {i})}$

W szczególności obejmuje to klasyfikację spacji . Więc spacje ${\ Displaystyle S ^ {1} \ simeq K (\ mathbb {Z}, 1)}$ , ${\ Displaystyle \ mathbb { CP} ^{\infty }\simeq K(\mathbb {Z} ,2)}$ i nieskończone przestrzenie soczewek ${\ Displaystyle L_ {q} ^ {\ infty} \ simeq K (\ mathbb {Z} / q, 2)}$ odpowiadają zespołom Kan pewnego zbioru uproszczonego. W rzeczywistości zestaw ten można skonstruować jawnie, używając zgodności Dolda-Kana kompleksu łańcuchowego i biorąc podstawowy zestaw uproszczony uproszczonej grupy abelowej.

Geometryczne realizacje małych grupoid

Innym ważnym źródłem przykładów są uproszczone zestawy związane z $małą$ . Jest to definiowane jako geometryczna realizacja zbioru uproszczonego i jest zwykle oznaczane jako $}}]}$$mathcal {$ . Mogliśmy również zastąpić ${\ displaystyle {\ mathcal {G}}}$ z grupoidą nieskończoności. Przypuszcza się, że kategoria homotopii geometrycznych realizacji grup nieskończonych jest równoważna kategorii homotopii typów homotopii. Nazywa się to hipotezą homotopii.

Non-przykład: standardowy n-simplex

Okazuje się, że standard $\ Delta ^ {n}}$ jest kompleksem Kan ^{pg 38} ${ \$ displaystyle . Ogólnie rzecz biorąc, konstrukcję kontrprzykładu można znaleźć, patrząc na niskowymiarowy przykład, powiedzmy ${\ displaystyle \ Delta ^ {1}}$ . Biorąc mapę ${\ Displaystyle \ Lambda _ {0} ^ {2} \ do \ Delta ^ {1}}$ wysyłanie

${\ Displaystyle {\ rozpocząć {macierz} [0,2] \ mapsto [0,0] i [0,1] \ mapsto [0,1 ]\end{macierz}}}$

$mapy$ kontrprzykład, ponieważ nie można go rozszerzyć na mapę, zachowywać Gdyby była mapa, trzeba by ją wysłać

${\ Displaystyle {\ rozpocząć {wyrównane} 0 \ mapsto 0 \\ 1 \ mapsto 1 \\ 2 \ mapsto 0 \ koniec {wyrównane}}}$

ale to nie jest mapa zbiorów uproszczonych.

Właściwości kategoryczne

Uproszczone wzbogacenie i kompleksy funkcyjne

$(X, Y)}$ { \ { $}$ gdzie uproszczenia są zdefiniowana jako

${\ Displaystyle {\ textbf {Hom}} _ {n} (X, Y) = {\ tekst {Hom}} _ {s {s \text{Zbiory}}}(X\razy \Delta ^{n},Y)}$

a dla mapy porządkowej istnieje mapa indukowana ${\ Displaystyle \ theta: [m] \ do [n]}$

${\ Displaystyle \ teta ^ {*}: {\ textbf {Hom}} (X, Y) _ {n} \ do {\ textbf { Dom}}(X,Y)_{m}}$

(ponieważ pierwszy czynnik Hom jest kontrawariantny) zdefiniowany przez wysłanie mapy do składu ${\ Displaystyle f: X \ razy \ Delta ^ {n} \ do Y$ }

${\ Displaystyle X \ razy \ Delta ^ {m} \ xrightarrow {1 \ razy \ teta} X \ razy \ Delta ^ {n} \ xrightarrow {f} Y}$

Prawo wykładnicze

Ten kompleks ma następujące wykładnicze prawo zbiorów uproszczonych

${\ Displaystyle {\ tekst {ev}} _ {*}: {\ tekst {Hom}} _ {s{\text{Zestawy}}}(K,{\textbf {Hom}}(X,Y))\to {\text{Hom}}_{s{\text{Zestawy}}}(X\razy K, Y)}$

który wysyła mapę do mapy złożonej ${\ Displaystyle f: K \ do {\ textbf {Hom}} (X, Y)}$

${\ Displaystyle X \ razy K \ xrightarrow {1 \ razy g} X \ razy {\ textbf {Hom}} (X, Y) \ xrightarrow {ev} Y}$

gdzie ${\ Displaystyle ev (x, f) = f (x, \ jota _ {n})}$ dla ${\ Displaystyle \ jota _ {n} \ in {\ tekst {Hom}} _ {\ Delta} ([n], [n])} podniesione do n$ - simpleksu ${\ Displaystyle \ Delta ^ {n.}}$ . ^

Fibracje Kana i cofnięcia

Biorąc pod uwagę fibrację (Kan) ⁱ włączenie zbiorów uproszczonych ja $\ hookrightarrow L}$$K$ istnieje fibracja

${\ Displaystyle {\ textbf {Hom}} (L, X) \ xrightarrow {(i^{*},p_{*})} {\textbf {Hom}}(K,X)\times _{{\textbf {Hom}}(K,Y)}{\textbf {Hom}} (L,Y)}$

(gdzie ${\ displaystyle {\ textbf {Hom}}}$ znajduje się w zespole funkcji w kategorii zbiorów uproszczonych) indukowany z diagramu przemiennego

${\ Displaystyle {\ rozpocząć {matryca}} {\ textbf {Hom }}(L,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(L,Y)\\i^{*}\strzałka w dół &&\strzałka w dół i^{*}\\{\ textbf {Hom}}(K,X)&\xrightarrow {p_{*}} &{\textbf {Hom}}(K,Y)\end{macierz}}}$

gdzie jest mapą wycofania podaną przez pre-composiiton i $.$$mapą$ pushforward podaną przez W szczególności poprzednie włóknienie implikuje ${\ Displaystyle p_ {*}: {\ textbf {Hom}} (L, X) \ do {\ textbf {Hom }}(L,Y)}$ i ${\ Displaystyle i ^ {*}: {\ textbf {Hom}} (L, Y) \ do {\ textbf {Hom}} (K, Y)} są fibracjami$ .

Aplikacje

Grupy homotopii kompleksów Kan

Grupy homotopii fibrantowego zbioru symplicalnego można zdefiniować kombinatorycznie za pomocą rogów, w sposób zgodny z grupami homotopii przestrzeni topologicznej, która to realizuje. Dla kompleksu Kan i wierzchołka $Displaystyle$$x: \ Delta ^ {0} \ do X}$ jako zbiór ${\ Displaystyle \ pi _ {n}(X,x)}$ jest zdefiniowane jako zbiór odwzorowań ${\ Displaystyle \ alpha: \ Delta ^ {n} \ do X}$ zestawów uproszczonych pasujących do pewnego diagramu przemiennego:

${\ Displaystyle \ pi _ {n} (X, x) = \ lewo \ {\ alpha :\Delta ^{n}\do X:{\begin{macierz}\Delta ^{n}&{\overset {\alpha }{\do }}&X\\\górna część &&\górna część x\\\częściowa \Delta ^{n}&\do &\Delta ^{0}\end{matrix}}\right\}}$

$odwzorowany$ fakt $B$${\ Displaystyle B ^ {n} / \ częściowe B ^ {n}}$ definicją kuli jako ilorazu dla standardowej piłki jednostkowej

${\ Displaystyle B ^ {n} = \ {x \ w \ mathbb {R} ^ {n}:||x ||_ {eu} \ równoważnik 1 \}}$

Zdefiniowanie struktury grupy wymaga nieco więcej pracy. $)$ mapy $\ Displaystyle (n + 1$ istnieje powiązany -simplice ${\ Displaystyle \ omega: \ Delta ^ {n + 1} \ do X}$ takie, że ${\ Displaystyle d_ {n} \ omega: \ Delta ^ {n} \ do X}$ daje ich dodatek. Ta mapa jest dobrze zdefiniowana aż do prostych klas homotopii map, co daje strukturę grupy. $2$ więcej, grupy $są$ dla } π $\ Displaystyle \ pi _ {0} (X)}$${\ Displaystyle [x]}$ jest zdefiniowany jako klasy homotopii map wierzchołków ${\ Displaystyle x: \ Delta ^ {0} \ do X}$ .

Grupy homotopii zbiorów uproszczonych

Korzystając z kategorii modeli, każdy zestaw uproszczony $ma$ zamiennik fibrantowy $który$ jest odpowiednikiem homotopii $uproszczonych$ homotopii zestawów Następnie grupy homotopii można zdefiniować jako ${\ displaystyle X}$

${\ Displaystyle \ pi _ {n} (X, x): = \ pi _ {n} ({\ kapelusz {X}}, { \kapelusz {x}})}$

gdzie ${\ Displaystyle {\ kapelusz {x}}}$ jest podniesieniem ${\ Displaystyle x: \ Delta ^ {0} \ do X}$ do ${\ Displaystyle {\ kapelusz {X} }}$ . Te zamienniki fibrantów można traktować jako topologiczny odpowiednik rozdzielczości kompleksu łańcuchowego (takiego jak rozdzielczość rzutowa lub rozdzielczość płaska ).

Zobacz też

• Kategoria modeli
• Uproszczona teoria homotopii
• Po prostu wzbogacona kategoria
• Słaby kompleks Kan (zwany także quasi-kategorią, ∞-kategorią)
• ∞-grupoida
• Fibracja zbiorów uproszczonych

• Podstawowe ilustrowane wprowadzenie do zbiorów uproszczonych

Bibliografia

•    Goerss, Paul G.; Jardine, John F. (1999). Uproszczona teoria homotopii . Bazylea: Birkäuser Bazylea. doi : 10.1007/978-3-0348-8707-6 . ISBN 978-3-0348-9737-2 . MR 1711612 .
•    Maj, J. Peter (1992) [1967]. Obiekty uproszczone w topologii algebraicznej . Wykłady z matematyki w Chicago. Chicago, IL: University of Chicago Press . ISBN 0-226-51180-4 . MR 1206474 .